向量结合复数:常曲率曲线(1)
By 苏剑林 | 2011-06-19 | 29429位读者 | 引用在之前的一篇向量系列的文章中,我们通过结合物理与向量来巧妙地推导出了曲线(包括平面和空间的)的曲率半径为
$$R=\frac{v^2}{a_c}=\frac{|\dot{\vec{r}}|^3}{|\dot{\vec{r}}\times \ddot{\vec{r}}|}\tag{1}$$
曲率则是曲率半径的导数:$\rho=\frac{1}{R}$。我们反过来思考一下:曲率恒定的平面曲线是否只有圆?
答案貌似是很显然的,我们需要证明一下。
由于只是考虑平面情况,我们先设$\dot{\vec{r}}=(v cos\theta,v sin\theta)=z=ve^{i\theta}$,代入(1)得到
$\frac{\dot{\theta}}{v}=\rho$————(2)
cos 1°的根式表达式
By 苏剑林 | 2011-06-26 | 57441位读者 | 引用BoJone记得自己第一次接触三角函数大概是小学五、六年级的时候,那时候我拿来了表姐的初中数学书来看。看到三角函数一章后,饶有兴致,希望能够找到一个根据角度来求三角函数值的方法,可是书本上只是教我去用计算器算和查表,这让我这个爱好计算的孩子大失所望。这个问题直到高一才得以解决,原来这已经涉及到了微积分中的泰勒级数了...
我记得为了求任意角度的三角函数值,我曾经根据30°、45°和60°的正弦值拟合过一条近似公式出来:
$$\sin A \approx \sqrt{\frac{A}{60}-1/4}$$
其中A以角度为单位,大致适用于25°~60°,精度好像有两位小数。当然,这个结果在今天看来是很粗糙的,但是这毕竟是我的“小学的作品”!在此留念一翻。
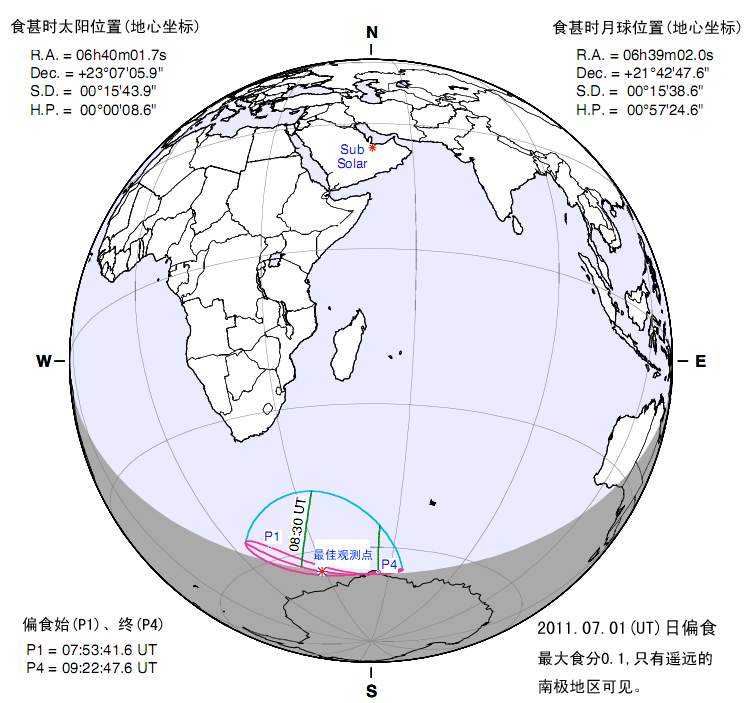
科学空间:2011年7月重要天象
By 苏剑林 | 2011-07-06 | 22873位读者 | 引用一道整数边三角形题目
By 苏剑林 | 2011-07-19 | 21217位读者 | 引用昨天在研究一个最优化问题时,遇到了一个这样的积分:
$$\int \frac{1}{\cos^3 \theta} d\theta$$
然后就顺便研究了一下这种类型的函数的积分。一般来讲,这类积分可以写成$\int cos^n \theta d\theta$或$\int sin^n \theta d\theta$,其中n是一个整数。
首先我们来解决n=1的情况,我们很容易就有$\int cos\theta d\theta=sin\theta +C$或$\int sin\theta d\theta=-cos\theta +C$,这是一个基本的结果。
如果n是大于1的正整数,那么可以用递推的方法来搞定:
关于e,i,π的那些鲜为人知的事儿...
By 苏剑林 | 2011-07-25 | 49948位读者 | 引用在农村,7月是忙碌的月份,农民们要忙着收割稻谷,收割完后要晒谷,同时还得准备“下秧”,准备新一轮的耕,BoJone家自然也不例外。不过我家田比较少(1亩左右),收割机几分钟搞定,谷也三两天就晒完了。不过在晒谷的时候,BoJone在考虑一个“收谷”问题:
晒谷时得先把成堆的谷子摊开,薄薄地平铺在平地上,等到傍晚或即将下雨时(这是最惨的情况,搞不好会淋谷)就将其收起来。问题就源于这里,一般来说我们会把谷均匀地铺成矩形,要把所有的谷都推到矩形里或外的哪一点上,才使得我们做功做小?
这个问题还可以推广开来,例如对于一地任意形状的谷子(如三角形),把它集中堆到哪个点最“轻松”?一堆固定质量的谷子,要把它平铺成什么形状,才使得收谷时最“轻松”?当然,这个问题的解不仅仅用于“收谷”,在很多规划建设中也可以应用到,例如要在一个人口大致均匀的城市中建设一个服务中心,这个服务中心应该建在哪里?这有点类似于我们之前讨论过的费马点问题 ,都是费马点只考虑了三个点的距离,而这个问题得考虑所有点的距离。
对称多项式不等式的“物理证明”
By 苏剑林 | 2011-08-13 | 35837位读者 | 引用本文将再次谈到对称这个话题,不过这一次的对象不是“等式”,而是“不等式”。
在数学研究中,我们经常会遇到各种各样的函数式子,其中有相当一部分是“对称”的。什么是对称的函数呢?对称有很多种说法,但是针对于多元对称式,我们的定义为满足$f(x_1,x_2,...,x_n)=f(y_1,y_2,...,y_n)$的函数,其中$(y_1,y_2,...,y_n)$是$(x_1,x_2,...,x_n)$的任意一个排列。通俗来讲,就是将式子中任意两个未知数交换位置,得到的式子还是和原来的式子一样。例如$\sin x+\sin y$,把$x,y$交换位置后得到$\sin y+\sin x$,还是和原来的一样;再如$xy+yz+zx$,将y,z互换后可以得到$xz+zy+yx$,结果还是和原式一样;等等。有些对称的函数是一个n次的多项式,那么就叫它为n次对称多项式,上边的例子$xz+zy+yx$就是一个三元二次对称多项式。








最近评论