变分自编码器(六):从几何视角来理解VAE的尝试
By 苏剑林 | 2020-09-10 | 108255位读者 |前段时间公司组织技术分享,轮到笔者时,大家希望我讲讲VAE。鉴于之前笔者也写过变分自编码器系列,所以对笔者来说应该也不是特别难的事情,因此就答应了下来,后来仔细一想才觉得犯难:怎么讲才好呢?
对于VAE来说,之前笔者有两篇比较系统的介绍:《变分自编码器(一):原来是这么一回事》和《变分自编码器(二):从贝叶斯观点出发》。后者是纯概率推导,对于不做理论研究的人来说其实没什么意义,也不一定能看得懂;前者虽然显浅一点,但也不妥,因为它是从生成模型的角度来讲的,并没有说清楚“为什么需要VAE”(说白了,VAE可以带来生成模型,但是VAE并不一定就为了生成模型),整体风格也不是特别友好。
笔者想了想,对于大多数不了解但是想用VAE的读者来说,他们应该只希望大概了解VAE的形式,然后想要知道“VAE有什么作用”、“VAE相比AE有什么区别”、“什么场景下需要VAE”等问题的答案,对于这种需求,上面两篇文章都无法很好地满足。于是笔者尝试构思了VAE的一种几何图景,试图从几何角度来描绘VAE的关键特性,在此也跟大家分享一下。
自编码器 #
我们从自编码器(AutoEncoder,AE)出发。自编码器的初衷是为了数据降维,假设原始特征$x$维度过高,那么我们希望通过编码器$E$将其编码成低维特征向量$z=E(x)$,编码的原则是尽可能保留原始信息,因此我们再训练一个解码器$D$,希望能通过$z$重构原始信息,即$x\approx D(E(x))$,其优化目标一般是
\begin{equation}E,D = \mathop{\text{argmin}}_{E,D}\mathbb{E}_{x\sim \mathcal{D}}\big[\Vert x - D(E(x))\Vert^2\big]\end{equation}
对应的示意图如下:
编码空间 #
假如每个样本都可以重构得很好,那么我们可以将$z$当作是$x$的等价表示,也就是说把$z$研究好了就相当于把$x$研究好了。现在我们将每个$x$都编码出对应的特征向量$z$,然后我们关心一个问题:这些$z$覆盖的空间“长什么样”?
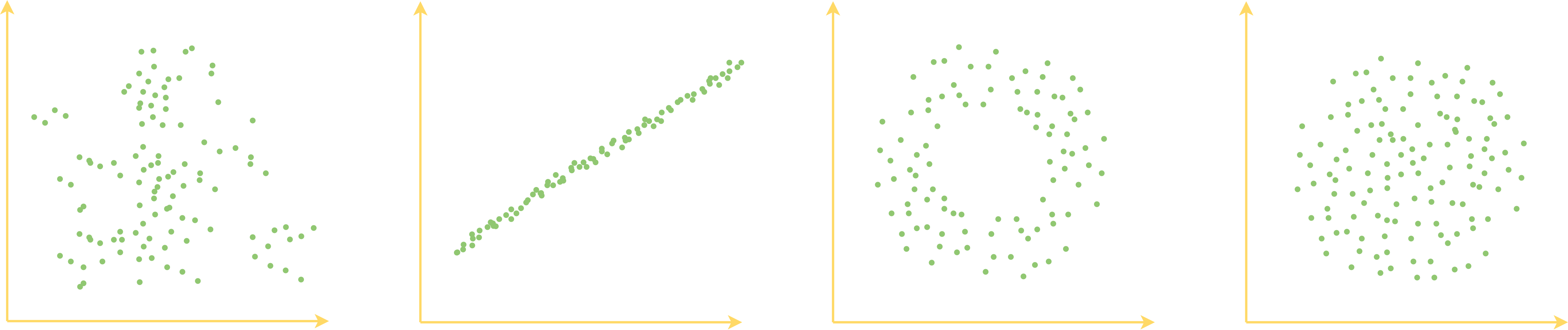
为什么要关心这个问题呢?因为我们可以有很多不同的编码方式,不同编码方式得到的特征向量也有好坏之分,从“编码空间长什么样”我们可以大致地看出特征向量的好坏。比如下面四个不同的编码向量的分布形状模拟图:
第一个图的向量分布没什么特别的形状,比较散乱,说明编码空间并不是特别规整;第二个图的向量集中在一条线上,说明其实编码向量的维度之间存在冗余;第三个图是一个环形,说明其圆心附近并没有对应的真实样本;第四个图是一个圆形,表明它比较规整地覆盖了一块连续空间。就四个图来看,我们认为最后一个图所描绘的向量分布形状是最理想的:规整、无冗余、连续,这意味着我们从中学习了一部分样本,就很容易泛化到未知的新样本上去,因为我们知道编码空间是规整连续的,所以我们知道训练样本的编码向量之间的“缝隙”(图中的两个点之间的空白部分),实际上也对应着未知的真实样本,因此把已知的搞好了,很可能未知的也搞好了。
从点到面 #
总的来说,大体上我们关心编码空间的如下问题:
1、所有编码向量覆盖一个怎样的区域?
2、是否有未知的真实样本对应空白之处的向量?
3、有没有“脱离群众”的向量?
4、有没有办法让编码空间更规整一些?
常规的自编码器由于没有特别的约束,因此很难回答上述问题。于是,变分自编码器出来了,从编码角度来看,它的目的是:1、让编码空间更规整一些;2、让编码向量更紧凑一些。为了达到这个目的,变分自编码器先引入了后验分布$p(z|x)$。
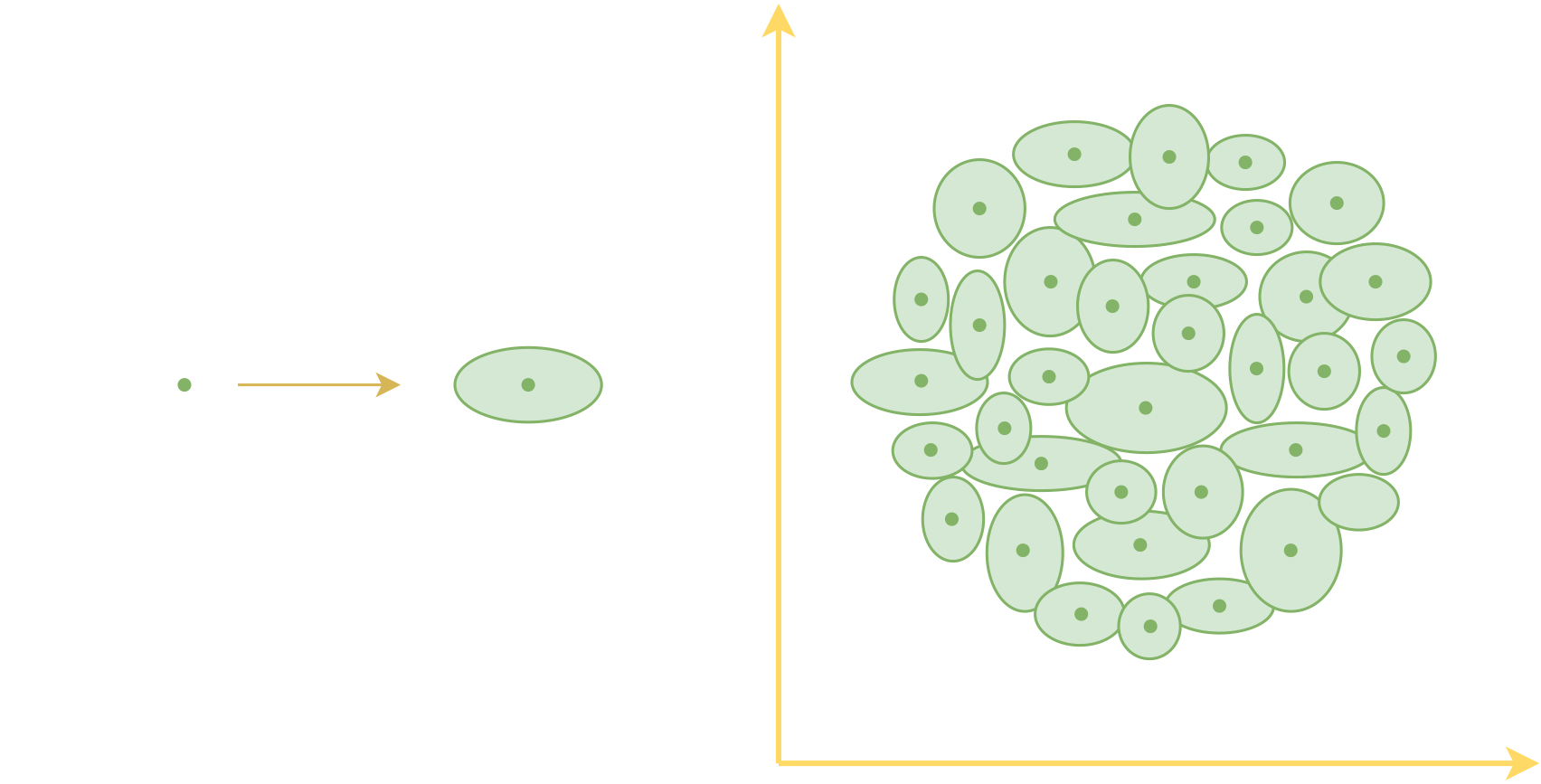
对于不想深究概率语言的读者来说,该怎么理解后验分布$p(z|x)$呢?直观来看,我们可以将后验分布理解为一个“椭圆”,原来每个样本对应着一个编码向量,也就是编码空间中的一个点,引入后验分布之后,相对于说现在每个样本$x$都对应一个“椭圆”。刚才我们说希望编码向量更“紧凑”一些,但理论上来讲,再多的“点”也没有办法把一个“面”覆盖完,但要是用“面”来覆盖“面”,那么就容易把目标覆盖住了。这就是变分自编码器做出的主要改动之一。
读者可能会问,为什么非得要椭圆呢?矩形或者其他形状可以吗?回到概率语言上,椭圆对应着“假设$p(z|x)$各分量独立的高斯分布”,从概率的角度来看,高斯分布是比较容易处理的一类概率分布,所以我们用高斯分布,也就对应着椭圆,其他形状也就对应这其他分布,比如矩形可以跟均匀分布对应,但后面再算KL散度的时候会比较麻烦,因此一般不使用。
采样重构 #
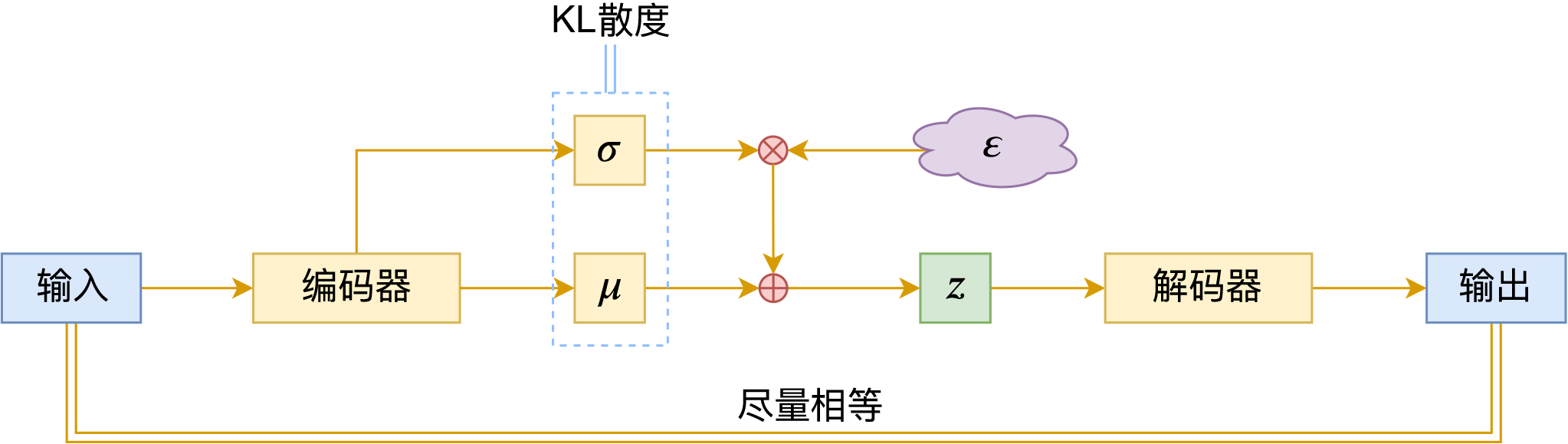
现在每个样本$x$都对应一个“椭圆”,而确定一个“椭圆”需要两个信息:椭圆中心、椭圆轴长,它们各自构成一个向量,并且这个向量依赖于样本$x$,我们将其记为$\mu(x),\sigma(x)$。既然整个椭圆都对应着样本$x$,我们要求椭圆内任意一点都可以重构$x$,所以训练目标为:
\begin{equation}\mu,\sigma,D = \mathop{\text{argmin}}_{\mu,\sigma,D}\mathbb{E}_{x\sim \mathcal{D}}\big[\Vert x - D(\mu(x) + \varepsilon\otimes \sigma(x))\Vert^2\big],\quad \varepsilon\sim \mathcal{N}(0, 1)\end{equation}
其中$\mathcal{D}$是训练数据,$\mathcal{N}(0, 1)$为标准正态分布,我们可以将它理解为一个单位圆,也就是说,我们先从单位圆内采样$\varepsilon$,然后通过平移缩放变换$\mu(x) + \varepsilon\otimes \sigma(x)$将其变为“中心为$\mu(x)$、轴长为$\sigma(x)$”的椭圆内的点,这个过程就是所谓的“重参数(Reparameterization)”。
这里的$\mu(x)$其实就对应于自编码器中的编码器$E(x)$,$\sigma(x)$相当于它能泛化的范围。
空间正则 #
最后,“椭圆”可以“让编码向量更紧凑”,但还不能“让编码空间更规整”。现在我们希望编码向量满足标准正态分布(可以将它理解为一个单位圆),即所有的椭圆覆盖的空间组成一个单位圆。
为此,我们希望每个椭圆都能向单位圆靠近,单位圆的中心为0,半径为1,所以一个基本想法是引入正则项:
\begin{equation}\mathbb{E}_{x\sim \mathcal{D}}\big[\Vert \mu(x) - 0\Vert^2 + \Vert \sigma(x) - 1\Vert^2\big]\end{equation}
事实上,这前面两项loss结合起来,就已经非常接近标准的变分自编码器了。标准的变分自编码器用了一个复杂一些、功能类似的正则项:
\begin{equation}\mathbb{E}_{x\sim \mathcal{D}}\left[\sum_{i=1}^d \frac{1}{2}\Big(\mu_{i}^2(x) + \sigma_{i}^2(x) - \log \sigma_{i}^2(x) - 1\Big)\right]\end{equation}
这个正则项来源于两个高斯分布的KL散度,所以通常也叫“KL散度项”。
将两项目标组合起来,就得到最终的变分自编码器了:
\begin{equation}\Vert x - D(\mu(x) + \varepsilon\otimes \sigma(x))\Vert^2 + \sum_{i=1}^d \frac{1}{2}\Big(\mu_{i}^2(x) + \sigma_{i}^2(x) - \log \sigma_{i}^2(x) - 1\Big), \quad \varepsilon\sim \mathcal{N}(0, 1)\end{equation}
文章总结 #
本文从几何类比的角度介绍了对变分自编码器(VAE)的理解,在此视角下,变分自编码器的目标是让编码向量更加紧凑,并规范了编码分布为标准正态分布(单位圆)。
这样一来,VAE能达到两个效果:1、从标准高斯分布(单位圆)随机采样一个向量,就可以由解码器得到真实样本,即实现了生成模型;2、由于编码空间的紧凑形以及训练时对编码向量所加入的噪声,使得编码向量的各个分量能做到一定程度的解耦,并赋予编码向量一定的线性运算性质。
几何视角能让我们快速地把握变分自编码器的关键特性,降低入门难度,但也有一定的不严谨之处。如有不妥当的地方,还请读者理解并指出。
转载到请包括本文地址:https://spaces.ac.cn/archives/7725
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Sep. 10, 2020). 《变分自编码器(六):从几何视角来理解VAE的尝试 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/7725
@online{kexuefm-7725,
title={变分自编码器(六):从几何视角来理解VAE的尝试},
author={苏剑林},
year={2020},
month={Sep},
url={\url{https://spaces.ac.cn/archives/7725}},
}












September 11th, 2020
一言蔽之,VAE 就是 AE 的贝叶斯化。把Z 的『点估计』 变成 Z 的概率分布P(z)的推断。对应你文中的『点』变成「椭圆」。就像以前经典的统计学习喜欢求解模型的最优解w, 而贝叶斯理论偏好求解模型参数w 的概率分布P(w)。所以VAE 更好的名字或许是 BAE(Bayesian auto encoder) :)
很正确的理解,其实就是估计点的同时估计它的不确定性。
September 30th, 2020
这个系列太赞了!第一次理解了VAE。我自己是按,5716->二->一->三->四->六,看的;但是似乎(六)很适合标记为(零)啊。
谢谢。
本篇的定位确实是“零”,不过编排是按照撰写时间顺序的,不调整了。
October 7th, 2020
博主好,最近看到LeCun 出了一篇 Implicit Rank-Minimizing Autoencoder
https://arxiv.org/abs/2010.00679
方法非常簡單,而且效果似乎比VAE 還好,
博主有空可以研究一下~
谢谢推荐,前几天已经收藏了,还没空看,到时候看看再说。
December 21st, 2020
博主好,读博主的文章受益匪浅~
我有个小小的问题,请问博主对“每个椭圆都能向单位圆靠近”与“所有的椭圆覆盖的空间组成一个单位圆”之间的联系有什么看法呢。
我看大部分有关VAE的文章都或多或少提及使整个编码分布服从标准正态分布,但损耗函数看上去是让每个具体的编码各自服从标准正态分布。这个差别是由损耗函数由变分下界推导来造成的吗,还是这两者是等价的呢?
请看本系列第二篇关于VAE的定量公式描述。
January 31st, 2021
相比CSDN上的,博主的文章要严谨的多。受益匪浅,感谢!
April 26th, 2021
太妙了,苏神这个VAE系列建议反过来看。。
August 30th, 2021
深入浅出,反复琢磨。
September 24th, 2021
您好!请问在“空间正则”中的“现在我们希望编码向量满足标准正态分布(可以将它理解为一个单位圆),即所有的椭圆覆盖的空间组成一个单位圆。”这句话,是应该按哪个思路理解:
1. 对于样本{X1, ..., Xn},每个样本对应的μ、σ,训练时在正态分布和标准正态分布之间对抗;
2. 对于样本{X1, ..., Xn},分别在单位圆采样、经过平移缩放变换得到{Z1, ..., Zn},让整个
{Z1, ..., Zn}服从标准正态分布;
也就是说,是将每个小椭圆趋向于单位圆,还是所有小椭圆组成的空间趋向于单位圆?
后者。
好的谢谢!
请问这个第二点是怎么体现的呢?在损失函数里看上去是让每个p(z|x)都向标准正态分布靠拢呀,感觉更像是第一点,如果是第二点该怎么结合公式进行理解呢?
人人都向雷锋学习,难道就一定可以让人人都跟雷锋一模一样么?
你要理解,就只看第二篇,优化联合分布的KL散度,就得到了连同重构项和KL散度项的一个整体loss,这个loss是整体,不能分割。
谢谢您的回答!
楼主的后者“ 对于样本{X1, ..., Xn},分别在单位圆采样、经过平移缩放变换得到{Z1, ..., Zn},让整个{Z1, ..., Zn}服从标准正态分布”,我不太理解这个后者中“所有小椭圆组成的空间趋向于单位圆”的含义以及如何表示。从正文看,您还提到了“希望每个椭圆都能向单位圆靠近”,这不是前者的含义吗?在第二篇里loss的第二项,是x不变将z视为变量得到的KL散度,这应该也对应着“希望每个椭圆都能向单位圆靠近”而不是“整个{Z1, ..., Zn}服从标准正态分布”吧,“整个{Z1, ..., Zn}服从标准正态分布”它们各自是一个高斯分布,怎么让这整个服从标准正态分布呢?
我说了,希望“人人向雷锋学习”,并不能保证“人人都跟雷锋一样”,只能实现“社会(人的总体)像雷锋一样(的风气)”。
重构项妨碍了每个椭圆像单位圆看齐,就好比每个人的个性妨碍了每个人跟雷锋一模一样。
@Lily|comment-20119 博主提到:希望“人人向雷锋学习”,并不能保证“人人都跟雷锋一样”,只能实现“社会(人的总体)像雷锋一样(的风气)”。
我自己理解的,反过来的几何化一点的表达是:让每个椭球都靠近标准圆,但是重构损失不允许椭球完全变成标准圆且要求椭球尽可能地不重叠。从解码器角度来看,进行了分布的叠加(即椭球的叠加)的“平均作用”后,它看到的样本极有可能就是等价来自于标准圆了。
多啰嗦一点,椭球的说明方式也能解释为什么VAE生成的图像模糊:椭球和椭球之间总会存在重叠的区域,当随机地从标准圆中采样得到的样本点处于这个重叠区域,那最后经过解码器解码出来的图像就会包含原来不同椭球所表示的图像的某些特征,也就是说解码出来的图像可以看做是多张图像的叠加效果,自然地图像就变得模糊了。
重叠这个角度可能不是很本质,因为如果在VAE的decoder端加上GAN Loss的话,是可能让重构和采样结果变得清晰的。
加GAN Loss为什么会使得结果图像变得清晰呢,博主可以讲一下吗,就是解码器是怎么使得处于重叠区域的采样点变得清晰的?我能想到的是,虽然有多张图像对应同一个编码$z$,GAN Loss会强迫解码器输出某种单一偏好的图像。
因为GAN学出来的判别器更符合我们对视觉相似的认知,弱化了L2距离带来的假设(逐像素对应),此外加Perceptual Loss也通常能提高清晰度,目前的Vision Tokenizer(如VQGAN)都是这样训的。早期GAN出来没多久那会,也有很多VAE+GAN的组合工作,来提高VAE的清晰度。
January 11th, 2024
怎么这么像3d gaussian...
公式(2)稍微有一点点类似。 每个样本是高斯球中心。 公式(3)就和3d高斯无关了。是为了采样方便把整体样本映射到一个标准高斯球。VAEloss结合了(2)和(3)一起算。
November 15th, 2024
高斯混合模型背后的假设是:数据来自K个高斯分布。
苏神的VAE博客看下来,VAE背后的假设似乎可以理解为,数据来自无穷个高斯分布,每个数据背后都对应一个高斯分布.
不知道这么理解是不是正确?
对的。VAE、GAN这类生成模型,可以理解为无限个高斯分布的叠加。