低秩近似之路（二）：SVD

上一篇文章中我们介绍了“伪逆”，它关系到给定矩阵$\boldsymbol{M}$和$\boldsymbol{A}$（或$\boldsymbol{B}$）时优化目标$\Vert \boldsymbol{A}\boldsymbol{B} - \boldsymbol{M}\Vert_F^2$的最优解。这篇文章我们来关注$\boldsymbol{A},\boldsymbol{B}$都不给出时的最优解，即
$$\begin{equation}\mathop{\text{argmin}}_{\boldsymbol{A},\boldsymbol{B}}\Vert \boldsymbol{A}\boldsymbol{B} - \boldsymbol{M}\Vert_F^2\label{eq:loss-ab}\end{equation}$$
其中$\boldsymbol{A}\in\mathbb{R}^{n\times r}, \boldsymbol{B}\in\mathbb{R}^{r\times m}, \boldsymbol{M}\in\mathbb{R}^{n\times m},r < \min(n,m)$。说白了，这就是要寻找矩阵$\boldsymbol{M}$的“最优$r$秩近似（秩不超过$r$的最优近似）”。而要解决这个问题，就需要请出大名鼎鼎的“SVD（奇异值分解）”了。虽然本系列把伪逆作为开篇，但它的“名声”远不如SVD，听过甚至用过SVD但没听说过伪逆的应该大有人在，包括笔者也是先了解SVD后才看到伪逆。

接下来，我们将围绕着矩阵的最优低秩近似来展开介绍SVD。

结论初探 #

对于任意矩阵$\boldsymbol{M}\in\mathbb{R}^{n\times m}$，都可以找到如下形式的奇异值分解（SVD，Singular Value Decomposition）：
$$\begin{equation}\boldsymbol{M} = \boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}\end{equation}$$
其中$\boldsymbol{U}\in\mathbb{R}^{n\times n},\boldsymbol{V}\in\mathbb{R}^{m\times m}$都是正交矩阵，$\boldsymbol{\Sigma}\in\mathbb{R}^{n\times m}$是非负对角矩阵：
$$\begin{equation}\boldsymbol{\Sigma}_{i,j} = \left\{\begin{aligned}&\sigma_i, &i = j \\ &0,&i \neq j\end{aligned}\right.\end{equation}$$
对角线元素默认从大到小排序，即$\sigma_1\geq \sigma_2\geq\sigma_3\geq\cdots\geq 0$，这些对角线元素就称为奇异值（Singular Value）。从数值计算角度看，我们可以只保留$\boldsymbol{\Sigma}$中非零元素，将$\boldsymbol{U},\boldsymbol{\Sigma},\boldsymbol{V}$的大小降低到$n\times r, r\times r, m\times r$（$r$是$\boldsymbol{M}$的秩），保留完整的正交矩阵则更便于理论分析。

SVD对于复矩阵同样成立，但需要将正交矩阵改为酉矩阵，转置改为共轭转置，但这里我们主要聚焦于跟机器学习关系更为密切的实矩阵结果。SVD的基础理论包括存在性、计算方法以及它与最优低秩近似的联系等，这些内容笔者后面都会给出自己的理解。

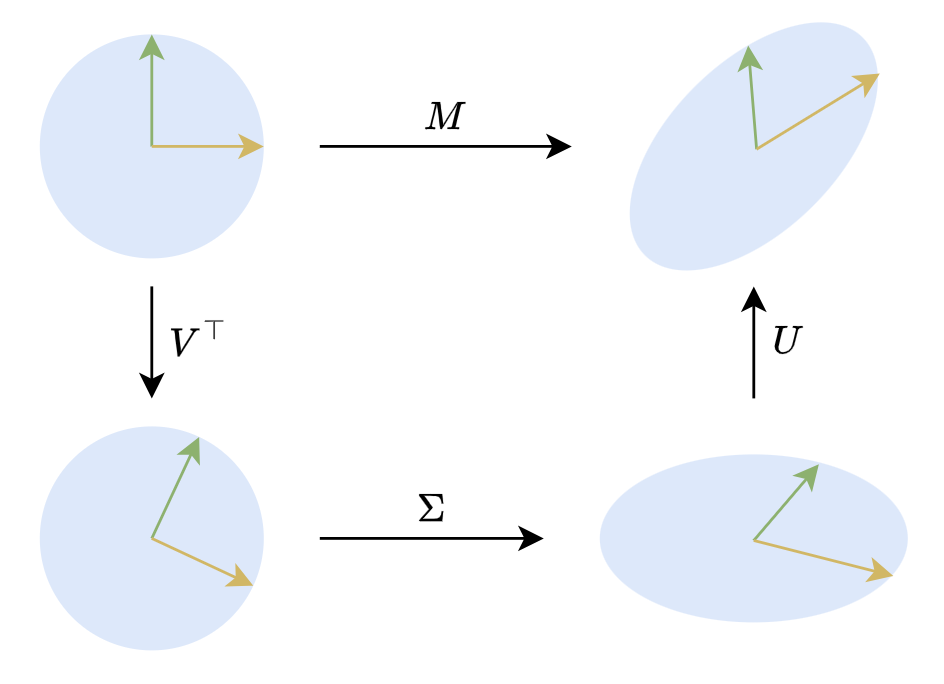
在二维平面下，SVD有非常直观的几何意义。二维的正交矩阵主要就是旋转（还有反射，但几何直观的话可以不那么严谨），所以$\boldsymbol{M}\boldsymbol{x}=\boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}\boldsymbol{x}$意味着任何对（列）向量$x$的线性变换，都可以分解为旋转、拉伸、旋转三个步骤，如下图所示：

SVD的几何意义

一些应用 #

不管是理论分析还是数值计算，SVD都有非常广泛的应用，其背后的原理之一是常用的矩阵/向量范数对正交变换具有不变性，所以SVD左右两个正交矩阵夹着中间一个对角矩阵的特点，往往能用来将很多矩阵相关的优化目标转换为等价的非负对角矩阵特例，起到简化问题的作用。

伪逆通解 #

以伪逆为例，当$\boldsymbol{A}\in\mathbb{R}^{n\times r}$的秩为$r$时，我们有
$$\begin{equation}\boldsymbol{A}^{\dagger} = \mathop{\text{argmin}}_{\boldsymbol{B}\in\mathbb{R}^{r\times n}}\Vert \boldsymbol{A}\boldsymbol{B} - \boldsymbol{I}_n\Vert_F^2\end{equation}$$
上一篇文章我们通过求导得出了$\boldsymbol{A}^{\dagger}$的表达式，然后又花了一些心思推广到$\boldsymbol{A}$的秩小于$r$的情形。但如果引入SVD的话，那么问题就简化得多了。我们可以将$\boldsymbol{A}$分解为$\boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}$，然后将$\boldsymbol{B}$表示成$\boldsymbol{V} \boldsymbol{Z} \boldsymbol{U}^{\top}$，注意我们没有规定$\boldsymbol{Z}$是对角阵，所以$\boldsymbol{B}=\boldsymbol{V} \boldsymbol{Z} \boldsymbol{U}^{\top}$总是可以做到的，于是
$$\begin{equation}\begin{aligned} \min_\boldsymbol{B}\Vert \boldsymbol{A}\boldsymbol{B} - \boldsymbol{I}_n\Vert_F^2 =&\, \min_\boldsymbol{Z}\Vert \boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}\boldsymbol{V} \boldsymbol{Z} \boldsymbol{U}^{\top} - \boldsymbol{I}_n\Vert_F^2 \\ =&\, \min_\boldsymbol{Z}\Vert \boldsymbol{U}(\boldsymbol{\Sigma} \boldsymbol{Z} - \boldsymbol{I}_n) \boldsymbol{U}^{\top}\Vert_F^2 \\ =&\, \min_\boldsymbol{Z}\Vert \boldsymbol{\Sigma} \boldsymbol{Z} - \boldsymbol{I}_n\Vert_F^2 \end{aligned}\end{equation}$$
最后一个等号是基于我们上一篇文章证明过的结论“正交变换不改变$F$范数”，这样我们就将问题简化成对角阵$\boldsymbol{\Sigma}$的伪逆了。接着我们可以用分块矩阵的形式将$\boldsymbol{\Sigma} \boldsymbol{Z} - \boldsymbol{I}_n$表示为
$$\begin{equation}\begin{aligned}\boldsymbol{\Sigma} \boldsymbol{Z} - \boldsymbol{I}_n =&\, \begin{pmatrix}\boldsymbol{\Sigma}_{[:r,:r]} \\ \boldsymbol{0}_{(n-r)\times r}\end{pmatrix} \begin{pmatrix}\boldsymbol{Z}_{[:r,:r]} & \boldsymbol{Z}_{[:r,r:]}\end{pmatrix} - \begin{pmatrix}\boldsymbol{I}_r & \boldsymbol{0}_{r\times(n-r)} \\ \boldsymbol{0}_{(n-r)\times r} & \boldsymbol{I}_{n-r}\end{pmatrix} \\ =&\, \begin{pmatrix}\boldsymbol{\Sigma}_{[:r,:r]}\boldsymbol{Z}_{[:r,:r]} - \boldsymbol{I}_r & \boldsymbol{\Sigma}_{[:r,:r]}\boldsymbol{Z}_{[:r,r:]}\\ \boldsymbol{0}_{(n-r)\times r} & -\boldsymbol{I}_{n-r}\end{pmatrix} \end{aligned}\end{equation}$$
这里的切片就按照Python数组的规则来理解。从最后的形式可以看出，要使得$\boldsymbol{\Sigma} \boldsymbol{Z} - \boldsymbol{I}_n$的$F$范数最小，唯一解是$\boldsymbol{Z}_{[:r,:r]}=\boldsymbol{\Sigma}_{[:r,:r]}^{-1}$，$\boldsymbol{Z}_{[:r,r:]}=\boldsymbol{0}_{r\times(n-r)}$，说白了，$\boldsymbol{Z}$就是将$\boldsymbol{\Sigma}^{\top}$的非零元素都取倒数然后转置，我们将它记为$\boldsymbol{\Sigma}^{\dagger}$，于是在SVD下就有
$$\begin{equation}\boldsymbol{A}=\boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}\quad\Rightarrow\quad \boldsymbol{A}^{\dagger} = \boldsymbol{V}\boldsymbol{\Sigma}^{\dagger}\boldsymbol{U}^{\top}\end{equation}$$
可以进一步证明这个结果也适用于秩小于$r$的$\boldsymbol{A}$，所以它是一个通用的形式，一些教程也直接将它作为伪逆的定义。此外，我们也可以观察到这个形式不区分左伪逆和右伪逆，这表明同一个矩阵的左伪逆和右伪逆是相等的，因此在说伪逆的时候不用特别区分左右。

矩阵范数 #

利用正交变换不改变$F$范数的结论，我们还可以得到
$$\begin{equation}\Vert \boldsymbol{M}\Vert_F^2 = \Vert \boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}\Vert_F^2 = \Vert \boldsymbol{\Sigma} \Vert_F^2 = \sum_{i=1}^{\min(n,m)}\sigma_i^2\end{equation}$$
也就是说奇异值的平方和等于$F$范数的平方。除了$F$范数外，SVD也可以用来计算“谱范数”。上一篇文章我们提到，$F$范数只是矩阵范数的一种，另一种常用的矩阵范数是基于向量的范数诱导出来的谱范数，它定义为：
$$\begin{equation}\Vert \boldsymbol{M}\Vert_2 = \max_{\Vert \boldsymbol{x}\Vert = 1} \Vert \boldsymbol{M}\boldsymbol{x}\Vert\end{equation}$$
注意等号右端出现的范数都是向量的范数（模长，$2$-范数），因此上述定义是明确的。由于它是向量的$2$-范数所诱导出来的，所以它也称为矩阵的$2$-范数。数值上，矩阵的谱范数等于它的最大奇异值，即$\Vert \boldsymbol{M}\Vert_2 = \sigma_1$。要证明这一点，只需要将$\boldsymbol{M}$做SVD为$\boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}$，然后代入谱范数的定义
$$\begin{equation}\max_{\Vert \boldsymbol{x}\Vert = 1} \Vert \boldsymbol{M}\boldsymbol{x}\Vert = \max_{\Vert \boldsymbol{x}\Vert = 1} \Vert \boldsymbol{U}\boldsymbol{\Sigma} (\boldsymbol{V}^{\top}\boldsymbol{x})\Vert = \max_{\Vert \boldsymbol{y}\Vert = 1} \Vert \boldsymbol{\Sigma} \boldsymbol{y}\Vert\end{equation}$$
第二个等号正是利用了正交矩阵不改变向量范数的特点。现在我们相当于将问题简化成为对角阵$\boldsymbol{\Sigma}$的谱范数，这个比较简单，设$\boldsymbol{y} = (y_1,y_2,\cdots,y_m)$，那么
$$\begin{equation}\Vert \boldsymbol{\Sigma} \boldsymbol{y}\Vert^2 = \sum_{i=1}^m \sigma_i^2 y_i^2 \leq \sum_{i=1}^m \sigma_1^2 y_i^2 = \sigma_1^2\sum_{i=1}^m y_i^2 = \sigma_1^2\end{equation}$$
所以$\Vert \boldsymbol{\Sigma} \boldsymbol{y}\Vert$不超过$\sigma_1$，并且$\boldsymbol{y}=(1,0,\cdots,0)$时取到等号，因此$\Vert \boldsymbol{M}\Vert_2=\sigma_1$。对比$F$范数的结果，我们还可以发现恒成立$\Vert \boldsymbol{M}\Vert_2\leq \Vert \boldsymbol{M}\Vert_F$。

低秩近似 #

最后我们再回到本文的主题最优低秩近似，也就是目标$\eqref{eq:loss-ab}$。将$\boldsymbol{M}$分解为$\boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}$，那么我们就可以写出
$$\begin{equation}\begin{aligned} \Vert \boldsymbol{A}\boldsymbol{B} - \boldsymbol{M}\Vert_F^2 =&\, \Vert \boldsymbol{U}\boldsymbol{U}^{\top}\boldsymbol{A}\boldsymbol{B}\boldsymbol{V}\boldsymbol{V}^{\top} - \boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}\Vert_F^2 \\ =&\, \Vert \boldsymbol{U}(\boldsymbol{U}^{\top}\boldsymbol{A}\boldsymbol{B}\boldsymbol{V} - \boldsymbol{\Sigma}) \boldsymbol{V}^{\top}\Vert_F^2 \\ =&\, \Vert \boldsymbol{U}^{\top}\boldsymbol{A}\boldsymbol{B}\boldsymbol{V} - \boldsymbol{\Sigma}\Vert_F^2 \end{aligned}\end{equation}$$
注意$\boldsymbol{U}^{\top}\boldsymbol{A}\boldsymbol{B}\boldsymbol{V}$仍可以代表任意秩不超过$r$的矩阵，所以通过SVD我们将矩阵$\boldsymbol{M}$的最优$r$秩近似简化成了非负对角阵$\boldsymbol{\Sigma}$的最优$r$秩近似。

在《对齐全量微调！这是我看过最精彩的LoRA改进（一）》中我们用同样思路求解过一个类似的优化问题：
$$\begin{equation}\mathop{\text{argmin}}_{\boldsymbol{A},\boldsymbol{B}} \Vert \boldsymbol{A}\boldsymbol{A}^{\top}\boldsymbol{M} + \boldsymbol{M}\boldsymbol{B}^{\top}\boldsymbol{B} - \boldsymbol{M}\Vert_F^2\end{equation}$$
利用SVD和正交变换不改变$F$范数，可以得到
$$\begin{equation}\begin{aligned} &\,\Vert \boldsymbol{A}\boldsymbol{A}^{\top}\boldsymbol{M} + \boldsymbol{M}\boldsymbol{B}^{\top}\boldsymbol{B} - \boldsymbol{M}\Vert_F^2 \\ =&\, \Vert \boldsymbol{A}\boldsymbol{A}^{\top}\boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top} + \boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}\boldsymbol{B}^{\top}\boldsymbol{B} - \boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}\Vert_F^2 \\ =&\, \Vert \boldsymbol{U}\boldsymbol{U}^{\top}\boldsymbol{A}\boldsymbol{A}^{\top}\boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top} + \boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}\boldsymbol{B}^{\top}\boldsymbol{B}\boldsymbol{V}\boldsymbol{V}^{\top} - \boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}\Vert_F^2 \\ =&\, \Vert \boldsymbol{U}[(\boldsymbol{U}^{\top}\boldsymbol{A})(\boldsymbol{U}^{\top}\boldsymbol{A})^{\top}\boldsymbol{\Sigma} + \boldsymbol{\Sigma} (\boldsymbol{B}\boldsymbol{V})^{\top} (\boldsymbol{B}\boldsymbol{V}) - \boldsymbol{\Sigma}] \boldsymbol{V}^{\top}\Vert_F^2 \\ =&\, \Vert (\boldsymbol{U}^{\top}\boldsymbol{A})(\boldsymbol{U}^{\top}\boldsymbol{A})^{\top}\boldsymbol{\Sigma} + \boldsymbol{\Sigma} (\boldsymbol{B}\boldsymbol{V})^{\top} (\boldsymbol{B}\boldsymbol{V}) - \boldsymbol{\Sigma}\Vert_F^2 \\ \end{aligned}\end{equation}$$
这就将原本一般矩阵$\boldsymbol{M}$的优化问题转化为$\boldsymbol{M}$是非负对角阵的特例，降低了分析难度。注意如果$\boldsymbol{A},\boldsymbol{B}$的秩不超过$r$，那么$\boldsymbol{A}\boldsymbol{A}^{\top}\boldsymbol{M} + \boldsymbol{M}\boldsymbol{B}^{\top}\boldsymbol{B}$的秩顶多为$2r$（假设$2r < \min(n,m)$），所以原始问题也是在求$\boldsymbol{M}$的最优$2r$秩近似，转化为非负对角阵后就是求非负对角阵的最优$2r$秩近似，跟前一个问题本质上是一样的。

理论基础 #

肯定了SVD的作用后，我们就需要补充一些理论证明了。首先要确保SVD的存在性，其次要找出至少一种计算方案，这样SVD的各种应用才算是切实可行的，接下来我们将用同一个过程把这两个问题一起解决掉。

谱之定理 #

在此之前，我们需要先引入一个“谱定理”，它既可以说是SVD的特例，也可以说是SVD的基础：

谱定理 对于任意实对称矩阵$\boldsymbol{M}\in\mathbb{R}^{n\times n}$，都存在谱分解（也称特征值分解） $$\begin{equation}\boldsymbol{M} = \boldsymbol{U}\boldsymbol{\Lambda} \boldsymbol{U}^{\top}\end{equation}$$ 其中$\boldsymbol{U},\boldsymbol{\Lambda}\in\mathbb{R}^{n\times n}$，$\boldsymbol{U}$是正交矩阵，$\boldsymbol{\Lambda}=\text{diag}(\lambda_1,\cdots,\lambda_n)$是对角矩阵。

说白了，谱定理就是断言任何实对称矩阵都可以被正交矩阵对角化，这基于如下两点性质：

1、实对称矩阵的特征值和特征向量都是实的；

2、实对称矩阵不同特征值对应的特征向量是正交的。

这两点性质的证明其实很简单，这里就不展开了。基于这两点我们可以立马得出，如果实对称矩阵$\boldsymbol{M}$有$n$个不同的特征值，那么谱定理成立：
$$\begin{equation}\begin{aligned} \boldsymbol{M}\boldsymbol{u}_1 = \lambda_1 \boldsymbol{u}_1 \\ \boldsymbol{M}\boldsymbol{u}_2 = \lambda_2 \boldsymbol{u}_2\\ \vdots \\ \boldsymbol{M}\boldsymbol{u}_n = \lambda_n \boldsymbol{u}_n\end{aligned} \quad\Rightarrow\quad \boldsymbol{M}\underbrace{(\boldsymbol{u}_1, \boldsymbol{u}_2, \cdots, \boldsymbol{u}_n)}_\boldsymbol{U} = \underbrace{(\boldsymbol{u}_1, \boldsymbol{u}_2, \cdots, \boldsymbol{u}_n)}_\boldsymbol{U}\underbrace{\begin{pmatrix}\lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \lambda_n \\ \end{pmatrix}}_{\boldsymbol{\Lambda}}\end{equation}$$
其中$\lambda_1,\lambda_2,\cdots,\lambda_n$是特征值，$\boldsymbol{u}_1,\boldsymbol{u}_2,\cdots,\boldsymbol{u}_n$是对应的单位特征（列）向量，写成矩阵乘法形式就是$\boldsymbol{M}\boldsymbol{U}=\boldsymbol{U}\boldsymbol{\Lambda}$，所以$\boldsymbol{M} = \boldsymbol{U}\boldsymbol{\Lambda} \boldsymbol{U}^{\top}$。证明的难点是如何拓展到有相等特征值的情形，但在思考完整的证明之前，我们可以先从一个不严谨的角度感受一下，这个不等特征值的结果是一定可以推广到一般情形的。

为什么这样说呢？从数值角度看，两个实数绝对相等的概率几乎为零，所以根本不需要考虑特征值相等的情形；用更数学的话说，那就是特征值不等的实矩阵在全体实矩阵中稠密，所以我们总可以找到一簇矩阵$\boldsymbol{M}_{\epsilon}$，当$\epsilon > 0$时它的特征值两两不等，当$\epsilon \to 0$时它等于$\boldsymbol{M}$。这样一来，每个$\boldsymbol{M}_{\epsilon}$我们都可以分解为$\boldsymbol{U}_{\epsilon}\boldsymbol{\Lambda} _{\epsilon}\boldsymbol{U}_{\epsilon}^{\top}$，取$\epsilon\to 0$就得到$\boldsymbol{M}$的谱分解。

数学归纳 #

不幸的是，上面这段话只能作为一个直观但不严谨的理解方式，因为将这段话转化为严格的证明还是很困难的。事实上，严格证明谱定理的最简单方法可能是数学归纳法，即在任意$n-1$阶实对称方阵都可以谱分解的假设上，我们证明$\boldsymbol{M}$也可以谱分解。

证明的关键思路是将$\boldsymbol{M}$分解为某个特征向量及其$n-1$维正交子空间，从而可以应用归纳假设。具体来说，设$\lambda_1$是$\boldsymbol{M}$的一个非零特征值，$\boldsymbol{u}_1$是对应的单位特征向量，那么有$\boldsymbol{M}\boldsymbol{u}_1 = \lambda_1 \boldsymbol{u}_1$，我们可以补充$n-1$个跟$\boldsymbol{u}_1$正交的单位向量$\boldsymbol{Q}=(\boldsymbol{q}_2,\cdots,\boldsymbol{q}_n)$，使得$(\boldsymbol{u}_1,\boldsymbol{q}_2,\cdots,\boldsymbol{q}_n)=(\boldsymbol{u}_1,\boldsymbol{Q})$成为一个正交矩阵。现在我们考虑
$$\begin{equation}(\boldsymbol{u}_1,\boldsymbol{Q})^{\top} \boldsymbol{M} (\boldsymbol{u}_1, \boldsymbol{Q}) = \begin{pmatrix}\boldsymbol{u}_1^{\top} \boldsymbol{M} \boldsymbol{u}_1 & \boldsymbol{u}_1^{\top} \boldsymbol{M} \boldsymbol{Q} \\ \boldsymbol{Q}^{\top} \boldsymbol{M} \boldsymbol{u}_1 & \boldsymbol{Q}^{\top} \boldsymbol{M} \boldsymbol{Q}\end{pmatrix} = \begin{pmatrix}\lambda_1 & \boldsymbol{0}_{1\times (n-1)} \\ \boldsymbol{0}_{(n-1)\times 1} & \boldsymbol{Q}^{\top} \boldsymbol{M} \boldsymbol{Q}\end{pmatrix}\end{equation}$$
注意到$\boldsymbol{Q}^{\top} \boldsymbol{M} \boldsymbol{Q}$是一个$n-1$阶方阵，并且很明显是一个实对称矩阵，所以根据假设它可以谱分解为$\boldsymbol{V} \boldsymbol{\Lambda}_2 \boldsymbol{V}^{\top}$，这里$\boldsymbol{V}$是$n-1$阶正交矩阵，$\boldsymbol{\Lambda}_2$是$n-1$阶对角阵，那么我们有$(\boldsymbol{Q}\boldsymbol{V})^{\top} \boldsymbol{M} \boldsymbol{Q}\boldsymbol{V}= \boldsymbol{\Lambda}_2$。根据这个结果，我们考虑$\boldsymbol{U} = (\boldsymbol{u}_1, \boldsymbol{Q}\boldsymbol{V})$，可以验证它也是一个正交矩阵，并且
$$\begin{equation}\boldsymbol{U}^{\top}\boldsymbol{M} \boldsymbol{U} = (\boldsymbol{u}_1,\boldsymbol{Q}\boldsymbol{V})^{\top} \boldsymbol{M} (\boldsymbol{u}_1, \boldsymbol{Q}\boldsymbol{V}) = \begin{pmatrix}\lambda_1 & \boldsymbol{0}_{1\times (n-1)} \\ \boldsymbol{0}_{(n-1)\times 1} & \boldsymbol{\Lambda}_2\end{pmatrix}\end{equation}$$
也就是说$\boldsymbol{U}$正是可以将$\boldsymbol{M}$对角化的正交矩阵，所以$\boldsymbol{M}$可以完成谱分解，这就完成了数学归纳法最关键的一步。

奇异分解 #

至此，所有准备工作都已经就绪，我们可以正式证明SVD的存在性，并给出一个实际计算的方案。

上一节我们引入了谱分解，不难发现它跟SVD的相似性，但也有两点明显区别：1、谱分解只适用于实对称矩阵，SVD适用于任意实矩阵；2、SVD的对角阵$\boldsymbol{\Sigma}$是非负的，但谱分解的$\boldsymbol{\Lambda}$则未必。那么，它们具体联系是什么呢？容易验证，如果$\boldsymbol{M}$的SVD为$\boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}$，那么
$$\begin{equation}\begin{aligned} \boldsymbol{M}\boldsymbol{M}^{\top} = \boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}\boldsymbol{V}\boldsymbol{\Sigma}^{\top} \boldsymbol{U}^{\top} = \boldsymbol{U}\boldsymbol{\Sigma}\boldsymbol{\Sigma}^{\top} \boldsymbol{U}^{\top}\\ \boldsymbol{M}^{\top}\boldsymbol{M} = \boldsymbol{V}\boldsymbol{\Sigma}^{\top} \boldsymbol{U}^{\top}\boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top} = \boldsymbol{V}\boldsymbol{\Sigma}^{\top}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}\\ \end{aligned}\end{equation}$$
注意到$\boldsymbol{\Sigma}\boldsymbol{\Sigma}^{\top}$和$\boldsymbol{\Sigma}^{\top}\boldsymbol{\Sigma}$都是对角阵，所以这意味着$\boldsymbol{M}\boldsymbol{M}^{\top}$和$\boldsymbol{M}^{\top}\boldsymbol{M}$的谱分解分别是$\boldsymbol{U}\boldsymbol{\Sigma}^2 \boldsymbol{U}^{\top}$和$\boldsymbol{V}\boldsymbol{\Sigma}^2 \boldsymbol{V}^{\top}$。这看起来将$\boldsymbol{M}\boldsymbol{M}^{\top}$、$\boldsymbol{M}^{\top}\boldsymbol{M}$分别做谱分解就可以得到$\boldsymbol{M}$的SVD了？确实没错，这可以作为SVD的一种计算方式，但我们无法直接通过它证明这样得出的$\boldsymbol{U},\boldsymbol{\Sigma},\boldsymbol{V}$满足$\boldsymbol{M}=\boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}$。

解决问题的关键是只对$\boldsymbol{M}\boldsymbol{M}^{\top}$或$\boldsymbol{M}^{\top}\boldsymbol{M}$之一做谱分解，然后通过另外的方法构造另一侧的正交矩阵。不失一般性，我们设$\boldsymbol{M}$的秩为$r \leq m$，考虑对$\boldsymbol{M}^{\top}\boldsymbol{M}$做谱分解为$\boldsymbol{V}\boldsymbol{\Lambda} \boldsymbol{V}^{\top}$，注意$\boldsymbol{M}^{\top}\boldsymbol{M}$是一个半正定矩阵，所以$\boldsymbol{\Lambda}$是非负的，并且假设对角线元素已经从大到小排列，秩$r$意味着只有前$r$个$\lambda_i$是大于0的，我们定义
$$\begin{equation}\boldsymbol{\Sigma}_{[:r,:r]} = (\boldsymbol{\Lambda}_{[:r,:r]})^{1/2},\quad \boldsymbol{U}_{[:n,:r]} = \boldsymbol{M}\boldsymbol{V}_{[:m,:r]}\boldsymbol{\Sigma}_{[:r,:r]}^{-1}\end{equation}$$
可以验证
$$\begin{equation}\begin{aligned} \boldsymbol{U}_{[:n,:r]}^{\top}\boldsymbol{U}_{[:n,:r]} =&\, \boldsymbol{\Sigma}_{[:r,:r]}^{-1}\boldsymbol{V}_{[:m,:r]}^{\top} \boldsymbol{M}^{\top}\boldsymbol{M}\boldsymbol{V}_{[:m,:r]}\boldsymbol{\Sigma}_{[:r,:r]}^{-1} \\ =&\, \boldsymbol{\Sigma}_{[:r,:r]}^{-1}\boldsymbol{V}_{[:m,:r]}^{\top} \boldsymbol{V}\boldsymbol{\Lambda} \boldsymbol{V}^{\top}\boldsymbol{V}_{[:m,:r]}\boldsymbol{\Sigma}_{[:r,:r]}^{-1} \\ =&\, \boldsymbol{\Sigma}_{[:r,:r]}^{-1}\boldsymbol{I}_{[:r,:m]}\boldsymbol{\Lambda} \boldsymbol{I}_{[:m,:r]}\boldsymbol{\Sigma}_{[:r,:r]}^{-1} \\ =&\, \boldsymbol{\Sigma}_{[:r,:r]}^{-1}\boldsymbol{\Lambda}_{[:r,:r]}\boldsymbol{\Sigma}_{[:r,:r]}^{-1} \\ =&\, \boldsymbol{I}_r \\ \end{aligned}\end{equation}$$
这里约定切片的优先级高于转置、求逆等矩阵运算，即$\boldsymbol{U}_{[:n,:r]}^{\top}=(\boldsymbol{U}_{[:n,:r]})^{\top}$、$\boldsymbol{\Sigma}_{[:r,:r]}^{-1}=(\boldsymbol{\Sigma}_{[:r,:r]})^{-1}$等。上述结果表明$\boldsymbol{U}_{[:n,:r]}$是正交矩阵的一部份。接着我们有
$$\begin{equation}\boldsymbol{U}_{[:n,:r]}\boldsymbol{\Sigma}_{[:r,:r]}\boldsymbol{V}_{[:m,:r]}^{\top} = \boldsymbol{M}\boldsymbol{V}_{[:m,:r]}\boldsymbol{\Sigma}_{[:r,:r]}^{-1}\boldsymbol{\Sigma}_{[:r,:r]}\boldsymbol{V}_{[:m,:r]}^{\top} = \boldsymbol{M}\boldsymbol{V}_{[:m,:r]}\boldsymbol{V}_{[:m,:r]}^{\top}\end{equation}$$
注意$\boldsymbol{M}\boldsymbol{V}\boldsymbol{V}^{\top} = \boldsymbol{M}$是恒成立的，而$\boldsymbol{V}_{[:m,:r]}$是$\boldsymbol{V}$的前$r$列，根据$\boldsymbol{M}^{\top}\boldsymbol{M}=\boldsymbol{V}\boldsymbol{\Lambda} \boldsymbol{V}^{\top}$我们有可以写出$(\boldsymbol{M}\boldsymbol{V})^{\top}\boldsymbol{M}\boldsymbol{V} = \boldsymbol{\Lambda}$，我们记$\boldsymbol{V}=(\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots,\boldsymbol{v}_m)$，那么就有$\Vert \boldsymbol{M}\boldsymbol{v}_i\Vert^2=\lambda_i$，由于秩$r$的设定，所以当$i > r$时$\lambda_i=0$，这意味着此时的$\boldsymbol{M}\boldsymbol{v}_i$实际上是一个零向量，所以
$$\begin{equation}\begin{aligned}\boldsymbol{M} = \boldsymbol{M}\boldsymbol{V}\boldsymbol{V}^{\top} =&\, (\boldsymbol{M}\boldsymbol{V}_{[:m,:r]}, \boldsymbol{M}\boldsymbol{V}_{[:m,r:]})\begin{pmatrix}\boldsymbol{V}_{[:m,:r]}^{\top} \\ \boldsymbol{V}_{[:m,r:]}^{\top}\end{pmatrix} \\[8pt] =&\, (\boldsymbol{M}\boldsymbol{V}_{[:m,:r]}, \boldsymbol{0}_{m\times(m-r)} )\begin{pmatrix}\boldsymbol{V}_{[:m,:r]}^{\top} \\ \boldsymbol{V}_{[:m,r:]}^{\top}\end{pmatrix}\\[8pt] =&\, \boldsymbol{M}\boldsymbol{V}_{[:m,:r]}\boldsymbol{V}_{[:m,:r]}^{\top} \end{aligned}\end{equation}$$
这表明$\boldsymbol{U}_{[:n,:r]}\boldsymbol{\Sigma}_{[:r,:r]}\boldsymbol{V}_{[:m,:r]}^{\top}=\boldsymbol{M}$，再结合$\boldsymbol{U}_{[:n,:r]}$是正交矩阵的一部分这一事实，我们已经得到了$\boldsymbol{M}$的SVD的关键部分，我们只需要将$\boldsymbol{\Sigma}_{[:r,:r]}$补零成$n\times m$大小的$\boldsymbol{\Sigma}$，将$\boldsymbol{U}_{[:n,:r]}$补全为$n\times n$的正交矩阵$\boldsymbol{U}$，那么就得到完整的SVD形式$\boldsymbol{M}=\boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}$。

近似定理 #

最后，别忘了我们的最终目标是开始的优化问题$\eqref{eq:loss-ab}$。有了SVD后，我们就可以给出答案了：

如果$\boldsymbol{M}\in\mathbb{R}^{n\times m}$的SVD为$\boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}$，那么$\boldsymbol{M}$的最优$r$秩近似为$\boldsymbol{U}_{[:n,:r]}\boldsymbol{\Sigma}_{[:r,:r]} \boldsymbol{V}_{[:m,:r]}^{\top}$。

这称为“Eckart-Young-Mirsky定理”。在介绍SVD应用的“低秩近似”一节中，我们表明通过SVD可以将一般矩阵的最优$r$秩近似问题简化为非负对角阵的$r$秩近似，所以“Eckart-Young-Mirsky定理”相当于说非负对角阵的最优$r$秩近似就是只保留对角线最大的$r$个元素的矩阵。

可能有读者认为“这难道不是显然成立吗？”，但事实是虽然结论很符合直觉，但它确实不是显然成立的。下面我们就聚焦于求解：
$$\begin{equation}\min_{\boldsymbol{A},\boldsymbol{B}}\Vert \boldsymbol{A}\boldsymbol{B} - \boldsymbol{\Sigma}\Vert_F^2\end{equation}$$
其中$\boldsymbol{A}\in\mathbb{R}^{n\times r}, \boldsymbol{B}\in\mathbb{R}^{r\times m}, \boldsymbol{\Sigma}\in\mathbb{R}^{n\times m},r < \min(n,m)$。如果给定$\boldsymbol{A}$的话，$\boldsymbol{B}$的最优解我们在上一篇文章中已经求出，结果是$\boldsymbol{A}^{\dagger} \boldsymbol{\Sigma}$，所以我们有
$$\begin{equation}\min_{\boldsymbol{A},\boldsymbol{B}}\Vert \boldsymbol{A}\boldsymbol{B} - \boldsymbol{\Sigma}\Vert_F^2 = \min_\boldsymbol{A}\Vert (\boldsymbol{A}\boldsymbol{A}^{\dagger} - \boldsymbol{I}_n)\boldsymbol{\Sigma}\Vert_F^2\end{equation}$$
设矩阵$\boldsymbol{A}$的SVD为$\boldsymbol{U}_\boldsymbol{A}\boldsymbol{\Sigma}_\boldsymbol{A} \boldsymbol{V}_\boldsymbol{A}^{\top}$，那么$\boldsymbol{A}^{\dagger}=\boldsymbol{V}_\boldsymbol{A} \boldsymbol{\Sigma}_\boldsymbol{A}^{\dagger} \boldsymbol{U}_\boldsymbol{A}^{\top}$，以及
$$\begin{equation}\begin{aligned} \Vert (\boldsymbol{A}\boldsymbol{A}^{\dagger} - \boldsymbol{I}_n)\boldsymbol{\Sigma}\Vert_F^2 =&\, \Vert (\boldsymbol{U}_\boldsymbol{A}\boldsymbol{\Sigma}_\boldsymbol{A} \boldsymbol{V}_\boldsymbol{A}^{\top}\boldsymbol{V}_\boldsymbol{A} \boldsymbol{\Sigma}_\boldsymbol{A}^{\dagger} \boldsymbol{U}_\boldsymbol{A}^{\top} - \boldsymbol{I}_n)\boldsymbol{\Sigma}\Vert_F^2 \\ =&\, \Vert (\boldsymbol{U}_\boldsymbol{A}\boldsymbol{\Sigma}_\boldsymbol{A} \boldsymbol{\Sigma}_\boldsymbol{A}^{\dagger} \boldsymbol{U}_\boldsymbol{A}^{\top} - \boldsymbol{I}_n)\boldsymbol{\Sigma}\Vert_F^2 \\ =&\, \Vert \boldsymbol{U}_\boldsymbol{A} (\boldsymbol{\Sigma}_\boldsymbol{A} \boldsymbol{\Sigma}_\boldsymbol{A}^{\dagger} - \boldsymbol{I}_n)\boldsymbol{U}_\boldsymbol{A}^{\top}\boldsymbol{\Sigma}\Vert_F^2 \\ =&\, \Vert (\boldsymbol{\Sigma}_\boldsymbol{A} \boldsymbol{\Sigma}_\boldsymbol{A}^{\dagger} - \boldsymbol{I}_n)\boldsymbol{U}_\boldsymbol{A}^{\top}\boldsymbol{\Sigma}\Vert_F^2 \\ \end{aligned}\end{equation}$$
由伪逆的计算公式知$\boldsymbol{\Sigma}_\boldsymbol{A} \boldsymbol{\Sigma}_\boldsymbol{A}^{\dagger}$是一个对角阵，并且对角线上前$r_\boldsymbol{A}$个元素为1（$r_\boldsymbol{A}\leq r$是$\boldsymbol{A}$的秩），其余都是0，所以$(\boldsymbol{\Sigma}_\boldsymbol{A} \boldsymbol{\Sigma}_\boldsymbol{A}^{\dagger} - \boldsymbol{I}_n)\boldsymbol{U}_\boldsymbol{A}^{\top}$相当于只保留正交矩阵$\boldsymbol{U}_\boldsymbol{A}^{\top}$的后$k=n-r_\boldsymbol{A}$行，所以最终可以简化成
$$\begin{equation}\min_\boldsymbol{A}\Vert (\boldsymbol{A}\boldsymbol{A}^{\dagger} - \boldsymbol{I}_n)\boldsymbol{\Sigma}\Vert_F^2 = \min_{k,\boldsymbol{U}}\Vert \boldsymbol{U}\boldsymbol{\Sigma}\Vert_F^2\quad\text{s.t.}\quad k\geq n-r, \boldsymbol{U}\in\mathbb{R}^{k\times n}, \boldsymbol{U}\boldsymbol{U}^{\top} = \boldsymbol{I}_k\end{equation}$$
现在根据$F$范数定义可以写出
$$\begin{equation}\Vert \boldsymbol{U}\boldsymbol{\Sigma}\Vert_F^2=\sum_{i=1}^k \sum_{j=1}^n u_{i,j}^2 \sigma_j^2 =\sum_{j=1}^n \sigma_j^2 \underbrace{\sum_{i=1}^k u_{i,j}^2}_{w_j}=\sum_{j=1}^n \sigma_j^2 w_j\end{equation}$$
注意到$0 \leq w_j \leq 1$，以及$w_1+w_2+\cdots+w_n = k$，在此约束下最右端的最小值只能是最小的$k$个$\sigma_j^2$之和，又因为$\sigma_j$已经从大到小排好序，所以
$$\begin{equation}\min_{k,\boldsymbol{U}}\Vert \boldsymbol{U}\boldsymbol{\Sigma}\Vert_F^2=\min_k \sum_{j=n-k+1}^n \sigma_j^2 = \sum_{j=r+1}^n \sigma_j^2\end{equation}$$
也就是说，$\boldsymbol{\Sigma}$与它的最优$r$秩近似的误差（$F$范数平方）是$\sum\limits_{j=r+1}^n \sigma_j^2$，这正好是保留对角线最大的$r$个元素后所产生的误差，所以我们证明了“非负对角阵的最优$r$秩近似就是只保留对角线最大的$r$个元素的矩阵”。当然，这只能说是一个解，我们没有否定多解的可能性。

值得指出的是，Eckart-Young-Mirsky定理不仅对$F$范数成立，还对谱范数成立，谱范数的证明实际上还简单一点，这里就不展开了，有兴趣的读者自行参考维基百科“Low-rank approximation”条目。

文章小结 #

本文的主角是声名显赫的SVD（奇异值分解），想必不少读者已经对它有所了解。在这篇文章中，我们主要围绕着SVD与低秩近似的相关内容进行展开，对SVD的存在性、计算以及与低秩近似的联系等理论内容给出了尽可能简单的证明过程。

转载到请包括本文地址：https://spaces.ac.cn/archives/10407

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。