自然数集中 N = ab + c 时 a + b + c 的最小值
By 苏剑林 | 2023-09-20 | 31326位读者 | 引用前天晚上微信群里有群友提出了一个问题:
对于一个任意整数$N > 100$,求一个近似算法,使得$N=a\times b+c$(其中$a,b,c$都是非负整数),并且令$a+b+c$尽量地小。
初看这道题,笔者第一感觉就是“这还需要算法?”,因为看上去自由度太大了,应该能求出个解析解才对,于是简单分析了一下之后就给出了个“答案”,结果很快就有群友给出了反例。这时,笔者才意识到这题并非那么平凡,随后正式推导了一番,总算得到了一个可行的算法。正当笔者以为这个问题已经结束时,另一个数学群的群友精妙地构造了新的参数化,证明了算法的复杂度还可以进一步下降!
整个过程波澜起伏,让笔者获益匪浅,遂将过程记录在此,与大家分享。
从EMD、WMD到WRD:文本向量序列的相似度计算
By 苏剑林 | 2020-05-13 | 51034位读者 | 引用在NLP中,我们经常要去比较两个句子的相似度,其标准方法是想办法将句子编码为固定大小的向量,然后用某种几何距离(欧氏距离、$\cos$距离等)作为相似度。这种方案相对来说比较简单,而且检索起来比较快速,一定程度上能满足工程需求。
此外,还可以直接比较两个变长序列的差异性,比如编辑距离,它通过动态规划找出两个字符串之间的最优映射,然后算不匹配程度;现在我们还有Word2Vec、BERT等工具,可以将文本序列转换为对应的向量序列,所以也可以直接比较这两个向量序列的差异,而不是先将向量序列弄成单个向量。
后一种方案速度相对慢一点,但可以比较得更精细一些,并且理论比较优雅,所以也有一定的应用场景。本文就来简单介绍一下属于后者的两个相似度指标,分别简称为WMD、WRD。
Earth Mover's Distance
本文要介绍的两个指标都是以Wasserstein距离为基础,这里会先对它做一个简单的介绍,相关内容也可以阅读笔者旧作《从Wasserstein距离、对偶理论到WGAN》。Wasserstein距离也被形象地称之为“推土机距离”(Earth Mover's Distance,EMD),因为它可以用一个“推土”的例子来通俗地表达它的含义。
[问题解答]运煤车的最大路程(更正)
By 苏剑林 | 2014-05-04 | 37046位读者 | 引用在农村,7月是忙碌的月份,农民们要忙着收割稻谷,收割完后要晒谷,同时还得准备“下秧”,准备新一轮的耕,BoJone家自然也不例外。不过我家田比较少(1亩左右),收割机几分钟搞定,谷也三两天就晒完了。不过在晒谷的时候,BoJone在考虑一个“收谷”问题:
晒谷时得先把成堆的谷子摊开,薄薄地平铺在平地上,等到傍晚或即将下雨时(这是最惨的情况,搞不好会淋谷)就将其收起来。问题就源于这里,一般来说我们会把谷均匀地铺成矩形,要把所有的谷都推到矩形里或外的哪一点上,才使得我们做功做小?
这个问题还可以推广开来,例如对于一地任意形状的谷子(如三角形),把它集中堆到哪个点最“轻松”?一堆固定质量的谷子,要把它平铺成什么形状,才使得收谷时最“轻松”?当然,这个问题的解不仅仅用于“收谷”,在很多规划建设中也可以应用到,例如要在一个人口大致均匀的城市中建设一个服务中心,这个服务中心应该建在哪里?这有点类似于我们之前讨论过的费马点问题 ,都是费马点只考虑了三个点的距离,而这个问题得考虑所有点的距离。
达尔文的进化学说告诉我们,自然界总是在众多的生物中挑出最能够适应环境的物种,赋予它们更高的生存几率,久而久之,这些物种经过亿万年的“优胜劣汰”,进化成了今天的千奇百怪的生物。无疑,经过长期的选择,优良的形状会被累积下来,换句话讲,这些物种在某些环境适应能力方面已经达到最优或近乎最优的状态(又是一个极值问题了)。好,现在我们来考虑蘑菇。
蘑菇是一种真菌生物,一般生长在阴暗潮湿的环境中。喜欢湿润的它自然也不希望散失掉过多的水分,因此,它努力地调整自身的形状,使它的“失水”尽可能地少。假设单位面积的蘑菇的失水速度是一致的,那么问题就变成了使一个给定体积的立体表面积尽可能少的问题了。并且考虑到水平各向同性生长的问题,理想的蘑菇形状应该就是一个平面图形的旋转体。那么这个旋转体是什么呢?聪明的你是否想到了是一个球体(的一部分)呢?
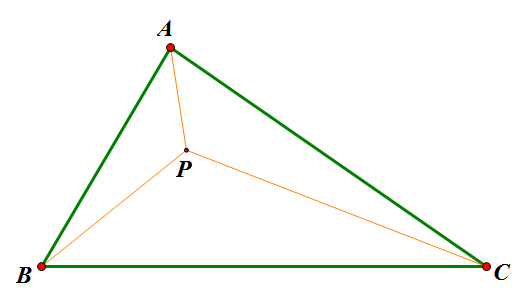
《自然极值》系列——4.费马点问题
By 苏剑林 | 2010-11-28 | 78078位读者 | 引用通过上面众多的文字描述,也许你还不大了解这两个原理有何美妙之处,也或者你已经迫不及待地想去应用它们却不知思路。为了不至于让大家产生“审美疲劳”,接下来我们将试图利用这两个原理对费马点问题进行探讨,看看原理究竟是怎么发挥作用的。运用的关键在于:如何通过适当的变换将其与光学或势能联系起来。
传统费马点问题是指在ΔABC中寻找点P,使得$AP+BP+CP$最小的问题;而广义的费马点则改成使$k_1 AP+k_2 BP+k_3 CP$最小。这是很具有现实意义的,是“在三个村庄之间建立一个中转站,如何才能使运送成为最低”之类的最优问题。我们将从光学和势能两个角度对这个问题进行探讨(也许有的读者已经阅读过了利用重力的原理来求解费马点,但是我想光学的方法依然会是你眼前一亮的。)









最近评论