n维空间下两个随机向量的夹角分布
By 苏剑林 | 2019-11-13 | 198412位读者 |昨天群里大家讨论到了$n$维向量的一些反直觉现象,其中一个话题是“一般$n$维空间下两个随机向量几乎都是垂直的”,这就跟二维/三维空间的认知有明显出入了。要从理论上认识这个结论,我们可以考虑两个随机向量的夹角$\theta$分布,并算算它的均值方差。
概率密度 #
首先,我们来推导$\theta$的概率密度函数。呃,其实也不用怎么推导,它是$n$维超球坐标的一个直接结论。
要求两个随机向量之间的夹角分布,很显然,由于各向同性,所以我们只需要考虑单位向量,而同样是因为各向同性,我们只需要固定其中一个向量,考虑另一个向量随机变化。不是一般性,考虑随机向量为
\begin{equation}\boldsymbol{x}=(x_1,x_2,\dots,x_n)\end{equation}
而固定向量为
\begin{equation}\boldsymbol{y}=(1,0,\dots,0)\end{equation}
将$\boldsymbol{x}$变换为超球坐标(关于$n$维球的知识可以参考维基百科):
\begin{equation}
\left\{\begin{aligned}
x_{1}&=\cos(\varphi_{1})\\
x_{2}&=\sin(\varphi_{1})\cos(\varphi_{2})\\
x_{3}&=\sin(\varphi_{1})\sin(\varphi_{2})\cos(\varphi_{3})\\
&\,\,\vdots \\
x_{n-1}&=\sin(\varphi_{1})\cdots \sin(\varphi_{n-2})\cos(\varphi_{n-1})\\
x_{n}&=\sin(\varphi_{1})\cdots \sin(\varphi_{n-2})\sin(\varphi_{n-1})
\end{aligned}\right.
\end{equation}
其中$\varphi_{n−1}\in [0, 2\pi)$而剩下的$\varphi$范围是$[0, \pi]$。此时,$\boldsymbol{x}$和$\boldsymbol{y}$的夹角是:
\begin{equation}\arccos \langle \boldsymbol{x},\boldsymbol{y}\rangle = \arccos \cos(\varphi_{1}) = \varphi_{1}
\end{equation}
也就是说两者的夹角正好是$\varphi_1$。那么,$\boldsymbol{x}$和$\boldsymbol{y}$的夹角不超过$\theta$的概率是:
\begin{equation}P_n(\varphi_1\leq\theta) = \frac{n\text{维超球面上}\varphi_1\text{不超过}\theta\text{的积分}}{n\text{维超球面上的全积分}}
\end{equation}
而$n$维超球面上的积分微元是$\sin^{n-2}(\varphi_{1})\sin^{n-3}(\varphi_{2})\cdots \sin(\varphi_{n-2})\,d\varphi_{1}\,d\varphi_{2}\cdots d\varphi_{n-1}$(可在维基百科找到),所以
\begin{equation}\begin{aligned}
P_n(\varphi_1\leq\theta) =& \frac{\int_0^{2\pi}\cdots\int_0^{\pi}\int_0^{\theta}\sin^{n-2}(\varphi_{1})\sin^{n-3}(\varphi_{2})\cdots \sin(\varphi_{n-2})\,d\varphi_{1}\,d\varphi_{2}\cdots d\varphi_{n-1}}{\int_0^{2\pi}\cdots\int_0^{\pi}\int_0^{\pi}\sin^{n-2}(\varphi_{1})\sin^{n-3}(\varphi_{2})\cdots \sin(\varphi_{n-2})\,d\varphi_{1}\,d\varphi_{2}\cdots d\varphi_{n-1}}\\
=&\frac{(n-1)\text{维单位超球的表面积}\times\int_0^{\theta}\sin^{n-2}\varphi_{1} d\varphi_1}{n\text{维单位超球的表面积}}\\
=&\frac{\Gamma\left(\frac{n}{2}\right)}{\Gamma\left(\frac{n-1}{2}\right)\sqrt{\pi}} \int_0^{\theta}\sin^{n-2}\varphi_1 d\varphi_1
\end{aligned}
\end{equation}
这表明$\theta$的概率密度函数就是
\begin{equation}
p_n(\theta) = \frac{\Gamma\left(\frac{n}{2}\right)}{\Gamma\left(\frac{n-1}{2}\right)\sqrt{\pi}}\sin^{n-2} \theta
\label{eq:theta}\end{equation}
有时候我们想关心$\eta=\cos\theta$的分布,这时候需要做一下概率密度的换元
\begin{equation}\begin{aligned}
p_n(\eta)=&\frac{\Gamma\left(\frac{n}{2}\right)}{\Gamma\left(\frac{n-1}{2}\right)\sqrt{\pi}}\sin^{n-2} (\arccos\eta)\left|\frac{d\theta}{d\eta}\right|\\
=&\frac{\Gamma\left(\frac{n}{2}\right)}{\Gamma\left(\frac{n-1}{2}\right)\sqrt{\pi}}(1-\eta^2)^{(n-3)/2}\\
\end{aligned}\label{eq:cos}\end{equation}
分布情况 #
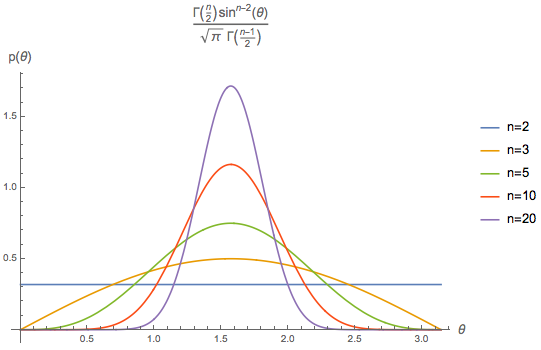
由$\eqref{eq:theta}$和$\eqref{eq:cos}$我们可以看到,当$n=2$时,夹角$\theta$的分布是一个均匀分布,而当$n=3$时,夹角余弦$\cos\theta$的分布是均匀分布。这两个结果说明在我们所能感知到的二维和三维空间中,角度的分布是比较均匀的。但是$n$比较大的时候呢?比如$n=20,50$?
从$p_n(\theta)\sim\sin^{n-2}\theta$的形式可以发现,当$n\geq 3$时,最大概率是$\theta=\frac{\pi}{2}$(即90度),另外$\sin^{n-2}\theta$也是关于$\theta=\frac{\pi}{2}$对称的,所以它的均值也是$\frac{\pi}{2}$。但这还不能充分描述分布情况,我们还需要考虑方差
\begin{equation}
Var_n(\theta) = \frac{\Gamma\left(\frac{n}{2}\right)}{\Gamma\left(\frac{n-1}{2}\right)\sqrt{\pi}}\int_0^{\pi}\left(\theta-\frac{\pi}{2}\right)^2\sin^{n-2} \theta d\theta\end{equation}
这个积分有解析解,但是形式很麻烦(喜欢看的话可以自己用Mathematica去算),我们来看部分数值解就好:
$$\begin{array}{c|c}
\hline
n & \text{方差}\\
\hline
3 & 0.467401\\
10 & 0.110661\\
20 & 0.0525832\\
50 & 0.0204053\\
100 & 0.0101007\\
200 & 0.00502508\\
1000 & 0.001001\\
\hline
\end{array}$$
可以看到,随着$n$的增大,方差越来越小,这意味着高维空间中任意两个向量的夹角几乎都集中在$\frac{\pi}{2}$附近,换言之,高维空间中任意两个向量几乎都是垂直的。
当然,从图像也可以看出:
如果想要近似解析解的读者,可以考虑用拉普拉斯方法,用一个高斯分布去近似$p_n(\theta)$:在$\theta=\frac{\pi}{2}$处对$\ln \sin^{n-2}\theta$进行展开
\begin{equation}\ln \sin^{n-2}\theta=\frac{2-n}{2}\left(\theta - \frac{\pi}{2}\right)^2 + \mathcal{O}\left(\left(\theta - \frac{\pi}{2}\right)^4\right)\end{equation}
即
\begin{equation}\sin^{n-2}\theta\approx \exp\left[-\frac{n-2}{2}\left(\theta - \frac{\pi}{2}\right)^2\right]\end{equation}
从这个近似形式看,我们可以近似地认为$\theta$服从均值为$\frac{\pi}{2}$、方差为$\frac{1}{n-2}$的正态分布,即当$n$较大时,方差近似为$\frac{1}{n-2}$,这也能看出$n$越大,方差越小。
文章小结 #
本文对高维空间的夹角分布进行了推导,记录在此以备忘,同时也供有需要的读者参考。
转载到请包括本文地址:https://spaces.ac.cn/archives/7076
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Nov. 13, 2019). 《n维空间下两个随机向量的夹角分布 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/7076
@online{kexuefm-7076,
title={n维空间下两个随机向量的夹角分布},
author={苏剑林},
year={2019},
month={Nov},
url={\url{https://spaces.ac.cn/archives/7076}},
}










April 13th, 2021
苏老师,您好。
我是一名通信专业学生,现在遇到一个问题,跟您这个主题有一点点关联,希望能得到您的答复。
问题如下,想要得到一些随机向量数据(用matlab或者python-numpy实现)。
generate some M-dimensional (complex-valued) vectors independently chosen from the isotropic distribution on the M-dimensional unit sphere.
下面这样做对吗?
```
x = sqrt(0.5)*(randn(M,1)+1i*randn(M,1));
x = x/norm(x);
```
np.random.random(shape)
May 26th, 2021
您好,我想请问一下,如果是在n维球面进行均匀采样的话(因为我需要固定点的坐标向量),是否还具有该性质呢(也就是任意两向量夹角趋于90度),谢谢。
存在啊,本文的推导假设本身就是球面均匀采样。
December 7th, 2021
苏神您好!能否推广一下结论,我想研究如下两件事情:
1)2K维空间下两个随机K维子空间的约当主角分布;
2)N维子空间下最多能塞下都少个K维子流形,使得两两最小夹角大于某个阈值$\theta$?
你这两个问题都有我不懂的概念...实在无能为力
苏老师可否留一下邮箱,我曾经通过投影给约当主角重新下了一个定义,并从另一个角度推出了和学术界基于瑞利商定义的相同的结果,可以分享给您,帮助您理解这个概念,然后有空一起交流?
谢谢,我对纯数学的讨论已经不大感兴趣,目前的结果够我用了~欢迎你写一篇公开的文章与大家一同分享。
你好,能和您交流下吗,我有个问题和您第二个问题很相似,即N个M维(N>>M)单位向量,两两之间的夹角最大是多少,我不是数学专业的,不知道这个要怎么计算的
咋联系你啊
最大夹角是pi啊;
如果问最大的最小夹角是多少,那就复杂了,参考Tammes Problem。
你是对的,我的问题有问题,我的意思就是两两之间最小夹角的最大值是多少的
January 11th, 2022
我邮箱是zkaiemail@163.com
July 25th, 2022
GAN模型往往用归一化的正态采样向量作为网络输入,这其实就是高维球面上均匀采样点。一个推论是来自概率论的正态分布和来自几何的欧式距离有着某种内在联系(因为都含平方?)。另外我顺带发现一个有意思的结论是,n维单位球当n->∞的时候,体积和表面积居然都是趋近于0的。
因为$n$维标准正态分布采样出来的向量,模长本身就非常接近$\sqrt{n}$,$n$越大,越集中在$\sqrt{n}$附近,所以模长本身就接近于固定了,再归一化一下,属于锦上添花。
油管上3b1b有个视频 解释了为什么Pi会出现在正态分布中,已经正态分布和圆/球为什么会有联系
February 26th, 2023
想问一下你们是否代表通过以余弦相似度作为损失函数的embedding向量的维度不应该太大
我不“代表”这件事,不过确实不需要太大,大了也可以用bert-whitening降维。
August 4th, 2023
如果说随着n增大,随机向量之间的夹角都接近pi/2,那是不是意味着,对于一个ffn参数的梯度,我们可以使用一个随机向量代替他,而不会导致结果下降?这好像和常理不太一样
训练好的参数与输入向量直观的关系,似乎不能认为是“随机”向量?
July 3rd, 2024
公式(10)
\begin{equation} \ln' \sin\theta => \frac{\cos\theta} {\sin\theta}
\\\ln'' \sin\theta => \frac{-\sin\theta} {\sin\theta}-\frac{\cos^2\theta} {\sin^2\theta}
\\泰勒公式在\frac{\pi}{2}展开 \ln\sin\theta = ln\sin\frac{\pi}{2} + \ln' \sin\frac{\pi}{2} *x + \ln'' \sin\frac{\pi}{2}*x^2/2! + \mathcal{O}
\\=0+0+(-1-0)\left(\theta - \frac{\pi}{2}\right)^2/2!+ \mathcal{O}
\\{(n-2)}\ln \sin\theta=\frac{2-n}{2}\left(\theta - \frac{\pi}{2}\right)^2 + \mathcal{O}\left(\left(\theta - \frac{\pi}{2}\right)^4\right)\end{equation}
整理后居然有高斯的形状。
其实就是在极值点展开,一阶项自动为零,所以展开到二阶得到一个二次函数。
November 13th, 2024
苏老师,您好。很荣幸最近可以拜读到您这篇文章,我最近在推导一个分布时遇到了与这个类似的情况。如果这里的n维向量是定义在复数域上,最后cos\theta的PDF应该如何推导呢?
我沿着您这篇文章给出的 \theta 以及cos\theta的PDF,推导出了(cos\theta)^2的分布,这是一个beta(1/2,(n-1)/2)。
如果是复数域上,(cos\theta)^2的分布是否会是beta(1,(n-1))?
$n$维复向量不能直接展开为$2n$维实向量来处理吗?
是可以的,苏老师。不过重点应该在设计两个复数向量,以来保证后面内积的结果可以写成某个角的余弦形式吧。我昨晚按照这个思路,写了一个稿子,还希望苏老师可以批评指正,我发您邮箱可以吗
可以,我尽量看看,但可能没那么快
好的,苏老师。我已发送至您spaces邮箱,请您查收!再次感谢苏老师可以批评指正
July 25th, 2025
苏神,这里随机向量的期望是不是要限制必须等于0,这个定理才成立呢,不为0,两个随机向量不是垂直的,而是成一个固定的角度。
噢,是这样的。“两个随机向量”肯定是依赖于分布的,但这里只考虑夹角,所以从直觉出发,先固定一个向量,另一个向量则从单位球面上均匀选取(保证各向同性),所以假设的是单位球面上的均匀分布。