低秩近似之路（四）：ID

这篇文章的主角是ID（Interpolative Decomposition），中文可以称之为“插值分解”，它同样可以理解为是一种具有特定结构的低秩分解，其中的一侧是该矩阵的若干列（当然如果你偏好于行，那么选择行也没什么问题），换句话说，ID试图从一个矩阵中找出若干关键列作为“骨架”（通常也称作“草图”）来逼近原始矩阵。

可能很多读者都未曾听说过ID，即便维基百科也只有几句语焉不详的介绍（链接），但事实上，ID跟SVD一样早已内置在SciPy之中（参考scipy.linalg.interpolative），这侧面印证了ID的实用价值。

基本定义 #

前三篇文章我们分别介绍了伪逆、SVD、CR近似，它们都可以视为寻找特定结构的低秩近似：
\begin{equation}\mathop{\text{argmin}}_{\text{rank}(\tilde{\boldsymbol{M}})\leq r}\Vert \tilde{\boldsymbol{M}} - \boldsymbol{M}\Vert_F^2\end{equation}
其中$\boldsymbol{M}\in\mathbb{R}^{n\times m}$。当不再添加其他约束时，最优解由SVD给出；当约定$\tilde{\boldsymbol{M}}=\boldsymbol{A}\boldsymbol{B}$并且$\boldsymbol{A},\boldsymbol{B}$之一已经给出求另一半的最优解时，最优解可以通过伪逆来给出；如果约定$\boldsymbol{M}=\boldsymbol{X}\boldsymbol{Y}$且$\tilde{\boldsymbol{M}}=\boldsymbol{X}_{[:, S]}\boldsymbol{Y}_{[S,:]}$，那么就是CR近似关心的问题。

CR近似通过选择原本矩阵的行/列来构建低秩近似，这使得近似结果更具解释性，同时也适用于一些非线性场景，但CR近似的前提是矩阵$\boldsymbol{M}$本身是由两个矩阵相乘而来，它的初衷是降低矩阵计算量，而对于直接给出矩阵$\boldsymbol{M}$的场景，类似的低秩近似则由ID给出。

具体来说，在ID中有$\tilde{\boldsymbol{M}}=\boldsymbol{C}\boldsymbol{Z}$，其中$\boldsymbol{C}=\boldsymbol{M}_{[:,S]}$是$\boldsymbol{M}$的若干列，$\boldsymbol{Z}$是任意的，即以$\boldsymbol{M}$若干列为骨架来逼近它自己：
\begin{equation}\mathop{\text{argmin}}_{S,\boldsymbol{Z}}\Vert \underbrace{\boldsymbol{M}_{[:,S]}}_{\boldsymbol{C}}\boldsymbol{Z} - \boldsymbol{M}\Vert_F^2\quad\text{s.t.}\quad S\subset\{0,1,\cdots,m-1\},|S|=r,\boldsymbol{Z}\in\mathbb{R}^{r\times m}\end{equation}
根据《低秩近似之路（一）：伪逆》的结果，如果$\boldsymbol{C}$已经确定，那么$\boldsymbol{Z}$的最优解就是$\boldsymbol{C}^{\dagger} \boldsymbol{M}$，所以ID的实际难度只有$S$的优化，即列的选取，这是一个组合优化问题，精确求解是NP-Hard的，所以主要目前是寻找效率和精度都适当的近似算法。

几何意义 #

在试图求解之前，我们先来进一步了解一下ID的几何意义，这有助于我们更好地理解它的应用场景和求解思路。我们先将$\boldsymbol{C}$表示为列向量形式$\boldsymbol{C}=(\boldsymbol{c}_1,\boldsymbol{c}_2,\cdots,\boldsymbol{c}_r)$，那么对于任意列向量$\boldsymbol{z}=(z_1,z_2,\cdots,z_r)^{\top}$，我们有
\begin{equation}\boldsymbol{C}\boldsymbol{z} = \begin{pmatrix}\boldsymbol{c}_1 & \boldsymbol{c}_2 & \cdots & \boldsymbol{c}_r\end{pmatrix}\begin{pmatrix}z_1 \\ z_2 \\ \vdots \\ z_r\end{pmatrix} = \sum_{i=1}^r z_i \boldsymbol{c}_i\end{equation}
所以$\boldsymbol{C}\boldsymbol{z}$的几何意义是$\boldsymbol{C}$的列向量的线性组合。注意$\boldsymbol{c}_1,\boldsymbol{c}_2,\cdots,\boldsymbol{c}_r$选自$\boldsymbol{M}=(\boldsymbol{m}_1,\boldsymbol{m}_2,\cdots,\boldsymbol{m}_m)$，所以ID就是说选择若干列作为（近似的）基向量，将剩下的列都表示为这些基的线性组合，这就是ID中的“I（Interpolative，插值）”的含义。

我们知道，“Interpolative”更准确的含义是“内插”，为了更好地突出“内插”这一特性，有些文献会给ID的定义加上$|z_{i,j}| \leq 1$的条件（$z_{i,j}$是矩阵$\boldsymbol{Z}$的任意元素）。当然这个条件实际上也比较苛刻，保证它严格成立的难度可能也是NP-Hard的，所以很多文献会将其放宽为$|z_{i,j}| \leq 2$，大多数近似算法的实际表现都能让这个界成立，如果没有其他需求，只考虑逼近误差的最优，那么也可以去掉这个限制。

QR分解 #

ID的求解算法分为确定性算法和随机算法两大类，其中确定性算法的计算量更大但近似程度往往更优，反之随机算法计算效率更高但精度稍次。注意它们都只是实际表现尚可的近似算法，并且都不排除有完全失效的极端例子的可能性。

第一个被视为标准的近似算法是基于QR分解的，更准确地说是Column-Pivoting的QR分解，中文常译作“列主元QR分解”（不过笔者感觉还不如干脆意译为“列驱QR分解”），它是一个确定性算法。为什么ID会跟QR分解联系在一起呢？我们可以从$\boldsymbol{Z}$的求法出发来理解。

前面提到，如果$\boldsymbol{C}$已经给定，那么$\boldsymbol{Z}$的最优解就是$\boldsymbol{C}^{\dagger}\boldsymbol{M}$，这个答案当然是对的，但不够直观。不失一般性，假设$\boldsymbol{c}_1,\boldsymbol{c}_2,\cdots,\boldsymbol{c}_r$线性无关，那么从几何的角度看，求$\boldsymbol{C}\boldsymbol{Z}$形式的最优近似实际上就是将$\boldsymbol{M}$的每个列向量都投影到$\boldsymbol{c}_1,\boldsymbol{c}_2,\cdots,\boldsymbol{c}_r$构成的$r$维子空间中，而为了求出这个投影结果，我们可以先将$\boldsymbol{c}_1,\boldsymbol{c}_2,\cdots,\boldsymbol{c}_r$执行Gram-Schmidt正交化，使其变为一组标准正交基，然后在标准正交基上投影就简单多了，而正交化的过程，自然就对应QR分解了。

Gram-Schmidt正交化是递归执行如下步骤：
\begin{equation}\boldsymbol{q}_1 = \frac{\boldsymbol{c}_1}{\Vert\boldsymbol{c}_1\Vert},\quad \boldsymbol{q}_k = \frac{\hat{\boldsymbol{q}}_k}{\Vert\hat{\boldsymbol{q}}_k\Vert},\quad\hat{\boldsymbol{q}}_k = \boldsymbol{c}_k - \sum_{i=1}^{k-1} (\boldsymbol{c}_k^{\top} \boldsymbol{q}_i)\boldsymbol{q}_i,\quad k = 2,3,\cdots,r\end{equation}
其结果将$\boldsymbol{C}$表示成：
\begin{equation}\boldsymbol{C} = \underbrace{\begin{pmatrix}\boldsymbol{q}_1 & \boldsymbol{q}_2 & \cdots & \boldsymbol{q}_r\end{pmatrix}}_{\boldsymbol{Q}}\underbrace{\begin{pmatrix}R_{1,1} & R_{1,2} & \cdots & R_{1,r} \\
0 & R_{2,2} & \cdots & R_{2,r} \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & R_{r,r} \\
\end{pmatrix}}_{\boldsymbol{R}}\end{equation}
有了$\boldsymbol{q}_1,\boldsymbol{q}_2,\cdots,\boldsymbol{q}_r$，那么矩阵$\boldsymbol{M}$的第$k$列$\boldsymbol{m}_k$在$\boldsymbol{C}$上的最优逼近和误差就分别是
\begin{equation}\sum_{i=1}^r (\boldsymbol{m}_k^{\top} \boldsymbol{q}_i)\boldsymbol{q}_i\qquad\text{和}\qquad \left\Vert\boldsymbol{m}_k - \sum_{i=1}^r (\boldsymbol{m}_k^{\top} \boldsymbol{q}_i)\boldsymbol{q}_i\right\Vert^2\end{equation}

列驱QR #

当然，上述结果是在已知$\boldsymbol{C}$的前提下得到的，那怎么从$\boldsymbol{M}$中挑出比较优的$r$列构成$\boldsymbol{C}$呢？列驱QR分解给出了一个参考答案。

一般来说，如果我们要对$\boldsymbol{m}_1,\boldsymbol{m}_2,\cdots,\boldsymbol{m}_m$做Gram-Schmidt正交化的话，都是按照顺序来的，即从$\boldsymbol{m}_1$出发，接下来是$\boldsymbol{m}_2,\boldsymbol{m}_3,\cdots$，而列驱QR分解则根据模长来修改了正交化顺序，写成公式是
\begin{equation}\begin{gathered}
\boldsymbol{q}_1 = \frac{\boldsymbol{m}_{\rho_1}}{\Vert\boldsymbol{m}_{\rho_1}\Vert},\quad
\boldsymbol{q}_k = \frac{\hat{\boldsymbol{q}}_k}{\Vert\hat{\boldsymbol{q}}_k\Vert},\quad\hat{\boldsymbol{q}}_k = \boldsymbol{m}_{\rho_k} - \sum_{i=1}^{k-1} (\boldsymbol{m}_{\rho_k}^{\top} \boldsymbol{q}_i)\boldsymbol{q}_i \\
\rho_1 = \mathop{\text{argmax}}_{i\in\{1,2,\cdots,m\}} \Vert \boldsymbol{m}_i\Vert,\quad \rho_k = \mathop{\text{argmax}}_{i\in\{1,2,\cdots,m\}\backslash\{\rho_1,\rho_2,\cdots,\rho_{k-1}\}} \left\Vert \boldsymbol{m}_i - \sum_{j=1}^{k-1} (\boldsymbol{m}_i^{\top} \boldsymbol{q}_j)\boldsymbol{q}_j\right\Vert
\end{gathered}\end{equation}
说白了，列驱QR分解就是每一步都选择剩下的误差最大的列来执行正交归一化。除了执行顺序有所变化外，列驱QR分解跟普通QR分解的计算并无其他不同之处，所以列驱QR分解的最终形式可以表示为
\begin{equation}\boldsymbol{M}\boldsymbol{\Pi} = \underbrace{\begin{pmatrix}\boldsymbol{q}_1 & \boldsymbol{q}_2 & \cdots & \boldsymbol{q}_m\end{pmatrix}}_{\boldsymbol{Q}}\underbrace{\begin{pmatrix}R_{1,1} & R_{1,2} & \cdots & R_{1,m} \\
0 & R_{2,2} & \cdots & R_{2,m} \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & R_{m,m} \\
\end{pmatrix}}_{\boldsymbol{R}}\end{equation}
其中$\boldsymbol{\Pi}$是列置换矩阵。根据每一步都选择误差（模长）最大列的操作，我们可以得到对于任意$k$，子矩阵$\boldsymbol{R}_{[k-1:,k-1:]}$的第一列模长是最大的，它不小于剩余任意一列的模长，即
\begin{equation}R_{k,k}^2 \geq \sum_{i=k}^j R_{i,j}^2,\quad \forall j = k,k+1,\cdots,m\end{equation}
由此还可以推得$|R_{1,1}|\geq |R_{2,2}| \geq \cdots\geq |R_{m,m}|$。这些性质让我们相信，如果想要$\boldsymbol{M}\boldsymbol{\Pi}$的一个$r$秩近似，只保留$\boldsymbol{R}$的前$r$行应该是一个不错的选择，即
\begin{equation}\boldsymbol{M}\boldsymbol{\Pi} = \boldsymbol{Q}\boldsymbol{R} \approx \boldsymbol{Q}_{[:,:r]}\boldsymbol{R}_{[:r,:]}=\boldsymbol{Q}_{[:,:r]}\big[\boldsymbol{R}_{[:r,:r]},\boldsymbol{R}_{[:r,r:]}\big]=\boldsymbol{Q}_{[:,:r]}\boldsymbol{R}_{[:r,:r]}\big[\boldsymbol{I}_r,\boldsymbol{R}_{[:r,:r]}^{-1}\boldsymbol{R}_{[:r,r:]}\big]\end{equation}
注意我们之前约定过切片的优先级高于求逆，所以这里$\boldsymbol{R}_{[:r,:r]}^{-1}$的含义是$(\boldsymbol{R}_{[:r,:r]})^{-1}$。不难发现$\boldsymbol{Q}_{[:,:r]}\boldsymbol{R}_{[:r,:r]}$实际上就是矩阵$\boldsymbol{M}$的$r$列，所以上式实际上给出了一个ID近似：
\begin{equation}\boldsymbol{M} \approx \boldsymbol{C}\boldsymbol{Z},\quad \boldsymbol{C}=\boldsymbol{Q}_{[:,:r]}\boldsymbol{R}_{[:r,:r]},\quad \boldsymbol{Z}=\big[\boldsymbol{I}_r,\boldsymbol{R}_{[:r,:r]}^{-1}\boldsymbol{R}_{[:r,r:]}\big]\boldsymbol{\Pi}^{\top}\end{equation}
以上就是基于列驱QR分解的ID求解算法，也是SciPy内置的求解算法（rand=False）。注意该算法是无法保证$|z_{i,j}| \leq 1$或者$|z_{i,j}| \leq 2$的，但根据很多文献的反馈，在实践中它几乎不会出现$|z_{i,j}| > 2$，所以这算是一个比较良好的求解算法。此外，SciPy也内置了列驱QR分解，在scipy.linalg.qr中设置pivoting=True即可打开。

随机求解 #

列驱QR分解每一步正交化操作，需要遍历剩余的所有向量取误差最大者，这在$m$很大时往往难以接受，另一方面如果$n$很大，那么模长、内积的计算量也会很高，于是随机算法便应运而生，它设法减少$n$或$m$的值来降低计算复杂度。

首先我们来看降低$n$的思路，即降低$\boldsymbol{M}$的每个列向量的维度，常用的方法是随机投影，跟《让人惊叹的Johnson-Lindenstrauss引理：理论篇》介绍的“JL引理”如出一辙。具体来说，假设$\boldsymbol{\Omega}\in\mathbb{R}^{d\times n}$是某个随机投影矩阵（其中$d\ll n$），它的元素是从某个分布如$\mathcal{N}(0,1/n)$独立重复采样出来的，那么我们考虑在小矩阵$\boldsymbol{\Omega}\boldsymbol{M}\in\mathbb{R}^{d\times m}$上执行列驱QR分解来确定被选中的$r$列的位置。更详细的介绍可以参考《Randomized algorithms for pivoting and for computing interpolatory and CUR factorizations》。

根据笔者有限的调研显示，SciPy求解ID的随机算法也是用的是类似思路，只是把随机采样的矩阵换成了更加结构化的“Subsampled Randomized Fourier Transform（SRFT）”，使得$\boldsymbol{\Omega}\boldsymbol{M}$这一步的计算量可以从$\mathcal{O}(mnd)$降到$\mathcal{O}(mn\log d)$。不过SRFT以及SciPy的实现细节笔者也不了解，有兴趣的读者可以参考《Enabling very large-scale matrix computations via randomization》、《A brief introduction to Randomized Linear Algebra》等资料进一步深究。

没有深究SRFT等复杂随机投影方法的另一个原因，是论文《Efficient Algorithms for Constructing an Interpolative Decomposition》发现更简单的列采样往往能得到更优的结果，而且还特别好理解，就是从$\boldsymbol{M}$中随机采样$k > r$列，然后用列驱QR分解从这$k$列中选出$r$列作为$\boldsymbol{C}$，最后再来根据$\boldsymbol{C}$求解$\boldsymbol{Z}$，这样就将列驱QR分解的矩阵大小从$n\times m$降低到$n\times k$。

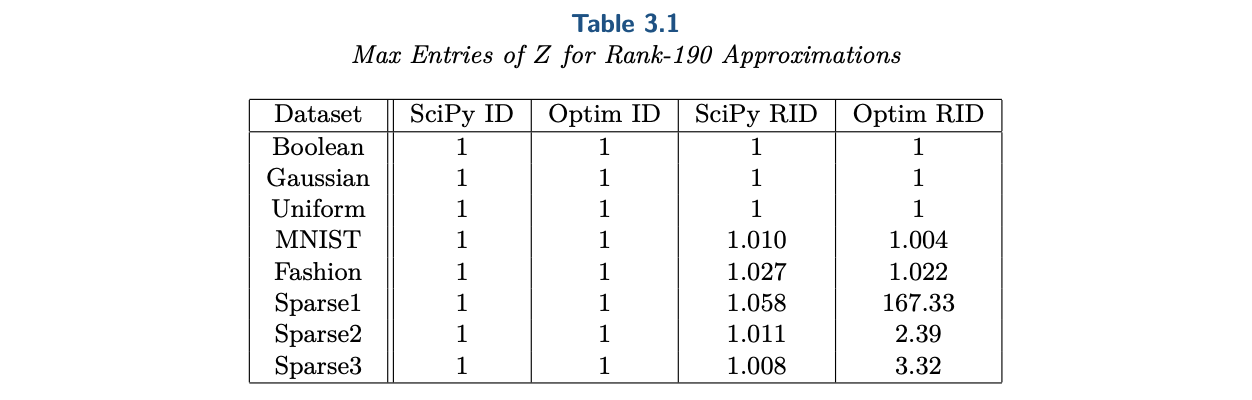
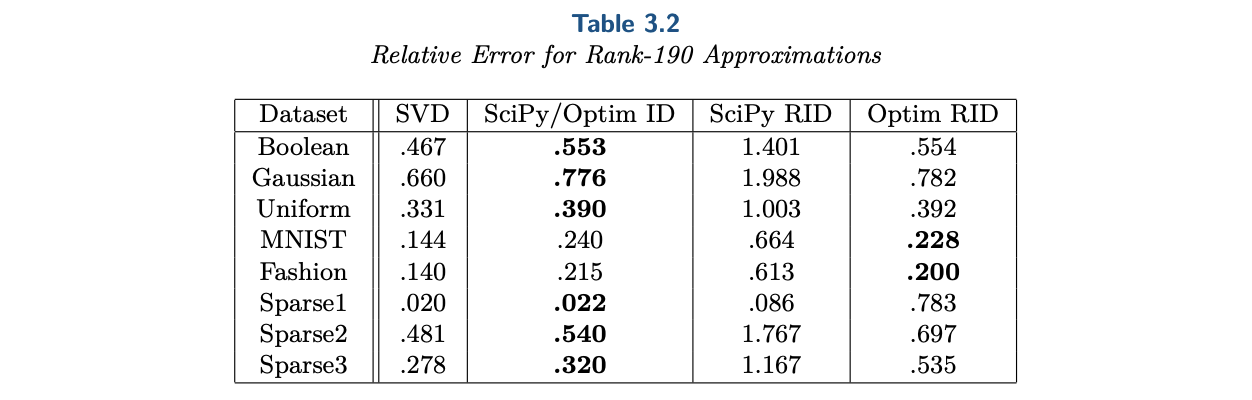
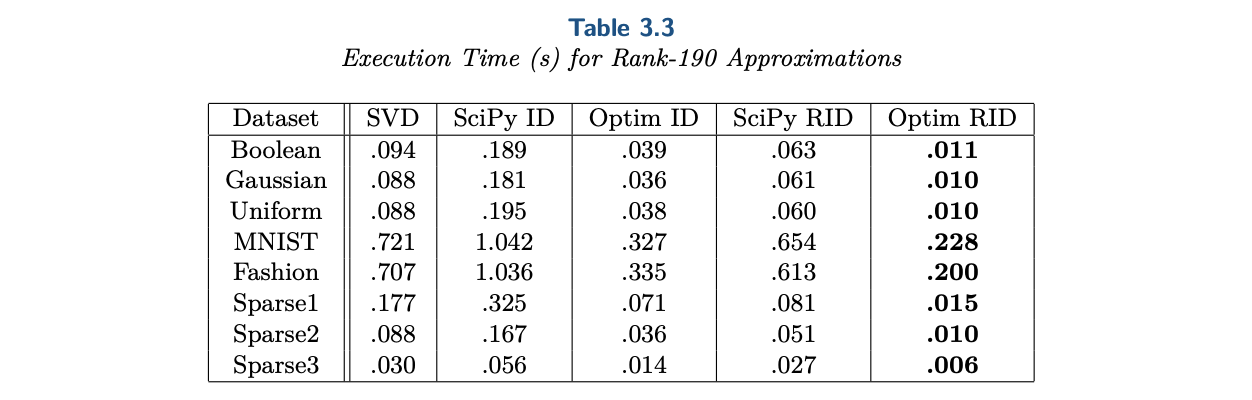
实验显示这样的简单思路顶多在个别任务上增大了$|z_{i,j}| > 2$的风险，但在误差上有明显优势：

提高精度 #

从上述表格可以留意到一个也许会让人觉得意外的结果：随机列采样的Optim-RID，在误差方面不仅优于同样是随机算法的SciPy-RID，在个别任务上甚至还优于确定性算法SciPy-ID和Optim-ID（它们数学上是等价的，都是基于完整的列驱QR分解，只是实现上的效率有所不同）。

这个看似反直觉的现象，实则说明了一个事实：列驱QR分解虽然可以作为ID的一个较好的baseline，但它选择基的能力可能跟随机选择差不了多少，列驱QR分解的主要作用只是保证大概率成立$|z_{i,j}| < 2$。其实这也不难理解，我们以$r=1$为例，这时候列驱QR分解就是返回模长最大的那一列，可是模长最大的那列一定是好的（能使得重构误差最小的）基底吗？显然不是，好的基底应该是多数向量共同指向的方向，模长最大不能体现这一点。

对于ID来说，列驱QR分解本质上是一种贪心算法，它将选$r$列贪心地转化为多个选$1$列的递归，而当$r=1$时，在$m$不算太大或者要求高精度的场景，通过枚举来精确求解的复杂度是可以接受的
\begin{equation}\mathop{\text{argmin}}_i \sum_{j=1}^m \left\Vert\boldsymbol{m}_j - \frac{(\boldsymbol{m}_j^{\top} \boldsymbol{m}_i)\boldsymbol{m}_i}{\Vert\boldsymbol{m}_i\Vert^2}\right\Vert^2\end{equation}
即遍历所有的$\boldsymbol{m}_i$，将剩下的所有列都投影到$\boldsymbol{m}_i$上来计算总误差，选择总误差最小的$\boldsymbol{m}_i$，其复杂度跟$m^2$成正比。如果将列驱QR分解每一步选择模长最大的操作改为选择总误差最小的上式，那么就能找出更好的基底，从而实现更低的重构误差（代价自然是复杂度更高了，而且更加无法保证$|z_{i,j}| < 2$了）。

总的来说，由于精确求解的NP-Hard性，所以ID有非常多的求解思路，上面列举的只是非常有限的几种，有兴趣的读者可以可以围绕着Randomized Linear Algebra、Column Subset Selection等关键词深入搜索。特别要指出的是，Randomized Linear Algebra，旨在通过随机方法来加速各种矩阵运算，本身已经成为了一个内容丰富的学科，本文的随机ID和上一篇基于采样的CR近似，都是这个学科的经典例子。

文章小结 #

本文介绍了ID（Interpolative Decomposition，插值分解），它通过从原矩阵中选择若干列来作为“骨架”来逼近原矩阵，是一种具有特定结构的低秩分解，几何意义相对来说更加直观，其核心难度是列的选择，本质上是一个NP-Hard的离散优化问题。

转载到请包括本文地址：https://spaces.ac.cn/archives/10501

更详细的转载事宜请参考：《科学空间FAQ》