节省显存的重计算技巧也有了Keras版了
By 苏剑林 | 2020-04-29 | 48050位读者 | 引用不少读者最近可能留意到了公众号文章《BERT重计算:用22.5%的训练时间节省5倍的显存开销(附代码)》,里边介绍了一个叫做“重计算”的技巧,简单来说就是用来省显存的方法,让平均训练速度慢一点,但batch_size可以增大好几倍。该技巧首先发布于论文《Training Deep Nets with Sublinear Memory Cost》,其实在2016年就已经提出了,只不过似乎还没有特别流行起来。
探索
公众号文章提到该技巧在pytorch和paddlepaddle都有原生实现了,但tensorflow还没有。但事实上从tensorflow 1.8开始,tensorflow就已经自带了该功能了,当时被列入了tf.contrib这个子库中,而从tensorflow 1.15开始,它就被内置为tensorflow的主函数之一,那就是tf.recompute_grad。
找到tf.recompute_grad之后,笔者就琢磨了一下它的用法,经过一番折腾,最终居然真的成功地用起来了,居然成功地让batch_size从48增加到了144!然而,在继续整理测试的过程中,发现这玩意居然在tensorflow 2.x是失效的...于是再折腾了两天,查找了各种资料并反复调试,最终算是成功地补充了这一缺陷。
最后是笔者自己的开源实现:
该实现已经内置在bert4keras中,使用bert4keras的读者可以升级到最新版本(0.7.5+)来测试该功能。
从EMD、WMD到WRD:文本向量序列的相似度计算
By 苏剑林 | 2020-05-13 | 57796位读者 | 引用在NLP中,我们经常要去比较两个句子的相似度,其标准方法是想办法将句子编码为固定大小的向量,然后用某种几何距离(欧氏距离、$\cos$距离等)作为相似度。这种方案相对来说比较简单,而且检索起来比较快速,一定程度上能满足工程需求。
此外,还可以直接比较两个变长序列的差异性,比如编辑距离,它通过动态规划找出两个字符串之间的最优映射,然后算不匹配程度;现在我们还有Word2Vec、BERT等工具,可以将文本序列转换为对应的向量序列,所以也可以直接比较这两个向量序列的差异,而不是先将向量序列弄成单个向量。
后一种方案速度相对慢一点,但可以比较得更精细一些,并且理论比较优雅,所以也有一定的应用场景。本文就来简单介绍一下属于后者的两个相似度指标,分别简称为WMD、WRD。
Earth Mover's Distance
本文要介绍的两个指标都是以Wasserstein距离为基础,这里会先对它做一个简单的介绍,相关内容也可以阅读笔者旧作《从Wasserstein距离、对偶理论到WGAN》。Wasserstein距离也被形象地称之为“推土机距离”(Earth Mover's Distance,EMD),因为它可以用一个“推土”的例子来通俗地表达它的含义。
鱼与熊掌兼得:融合检索和生成的SimBERT模型
By 苏剑林 | 2020-05-18 | 284692位读者 | 引用前段时间我们开放了一个名为SimBERT的模型权重,它是以Google开源的BERT模型为基础,基于微软的UniLM思想设计了融检索与生成于一体的任务,来进一步微调后得到的模型,所以它同时具备相似问生成和相似句检索能力。不过当时除了放出一个权重文件和示例脚本之外,未对模型原理和训练过程做进一步说明。在这篇文章里,我们来补充这部分内容。
UniLM
UniLM是一个融合NLU和NLG能力的Transformer模型,由微软在去年5月份提出来的,今年2月份则升级到了v2版本。我们之前的文章《从语言模型到Seq2Seq:Transformer如戏,全靠Mask》就简单介绍过UniLM,并且已经集成到了bert4keras中。
UniLM的核心是通过特殊的Attention Mask来赋予模型具有Seq2Seq的能力。假如输入是“你想吃啥”,目标句子是“白切鸡”,那UNILM将这两个句子拼成一个:[CLS] 你 想 吃 啥 [SEP] 白 切 鸡 [SEP],然后接如图的Attention Mask:
Google新作Synthesizer:我们还不够了解自注意力
By 苏剑林 | 2020-05-25 | 87413位读者 | 引用深度学习这个箱子,远比我们想象的要黑。
写在开头
据说物理学家费曼说过一句话[来源]:“谁要是说他懂得量子力学,那他就是真的不懂量子力学。”我现在越来越觉得,这句话中的“量子力学”也可以替换为“深度学习”。尽管深度学习已经在越来越多的领域证明了其有效性,但我们对它的解释性依然相当无力。当然,这几年来已经有不少工作致力于打开深度学习这个黑箱,但是很无奈,这些工作基本都是“马后炮”式的,也就是在已有的实验结果基础上提出一些勉强能说服自己的解释,无法做到自上而下的构建和理解模型的原理,更不用说提出一些前瞻性的预测。
本文关注的是自注意力机制。直观上来看,自注意力机制算是解释性比较强的模型之一了,它通过自己与自己的Attention来自动捕捉了token与token之间的关联,事实上在《Attention is All You Need》那篇论文中,就给出了如下的看上去挺合理的可视化效果:
但自注意力机制真的是这样生效的吗?这种“token对token”的注意力是必须的吗?前不久Google的新论文《Synthesizer: Rethinking Self-Attention in Transformer Models》对自注意力机制做了一些“异想天开”的探索,里边的结果也许会颠覆我们对自注意力的认知。
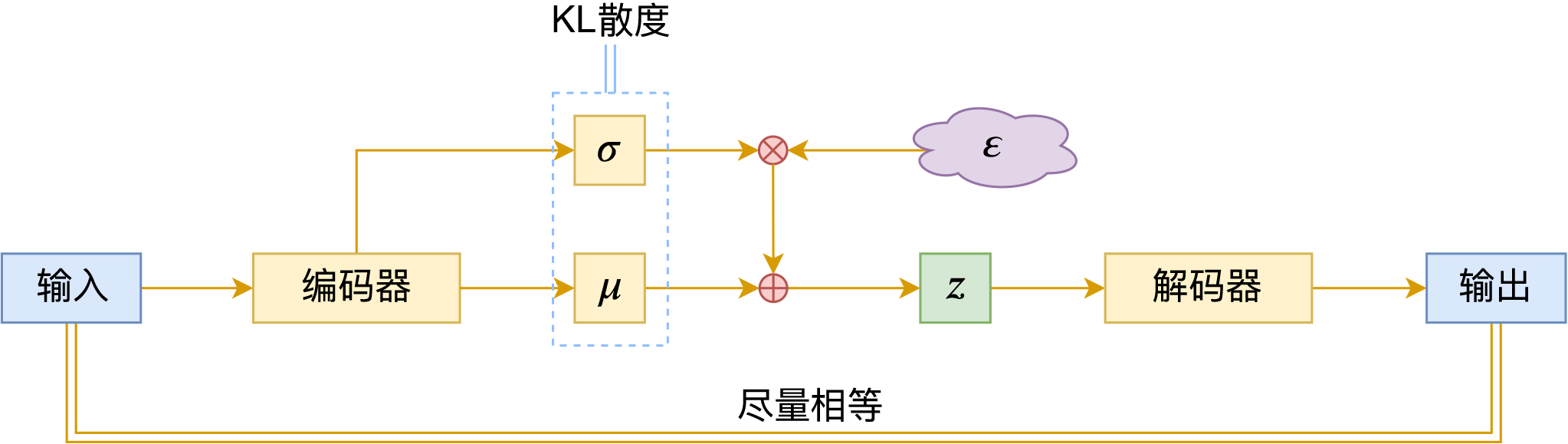
变分自编码器(六):从几何视角来理解VAE的尝试
By 苏剑林 | 2020-09-10 | 66280位读者 | 引用前段时间公司组织技术分享,轮到笔者时,大家希望我讲讲VAE。鉴于之前笔者也写过变分自编码器系列,所以对笔者来说应该也不是特别难的事情,因此就答应了下来,后来仔细一想才觉得犯难:怎么讲才好呢?
对于VAE来说,之前笔者有两篇比较系统的介绍:《变分自编码器(一):原来是这么一回事》和《变分自编码器(二):从贝叶斯观点出发》。后者是纯概率推导,对于不做理论研究的人来说其实没什么意义,也不一定能看得懂;前者虽然显浅一点,但也不妥,因为它是从生成模型的角度来讲的,并没有说清楚“为什么需要VAE”(说白了,VAE可以带来生成模型,但是VAE并不一定就为了生成模型),整体风格也不是特别友好。
笔者想了想,对于大多数不了解但是想用VAE的读者来说,他们应该只希望大概了解VAE的形式,然后想要知道“VAE有什么作用”、“VAE相比AE有什么区别”、“什么场景下需要VAE”等问题的答案,对于这种需求,上面两篇文章都无法很好地满足。于是笔者尝试构思了VAE的一种几何图景,试图从几何角度来描绘VAE的关键特性,在此也跟大家分享一下。
泛化性乱弹:从随机噪声、梯度惩罚到虚拟对抗训练
By 苏剑林 | 2020-06-01 | 96223位读者 | 引用提高模型的泛化性能是机器学习致力追求的目标之一。常见的提高泛化性的方法主要有两种:第一种是添加噪声,比如往输入添加高斯噪声、中间层增加Dropout以及进来比较热门的对抗训练等,对图像进行随机平移缩放等数据扩增手段某种意义上也属于此列;第二种是往loss里边添加正则项,比如$L_1, L_2$惩罚、梯度惩罚等。本文试图探索几种常见的提高泛化性能的手段的关联。
随机噪声
我们记模型为$f(x)$,$\mathcal{D}$为训练数据集合,$l(f(x), y)$为单个样本的loss,那么我们的优化目标是
\begin{equation}\mathop{\text{argmin}}_{\theta} L(\theta)=\mathbb{E}_{(x,y)\sim \mathcal{D}}[l(f(x), y)]\end{equation}
$\theta$是$f(x)$里边的可训练参数。假如往模型输入添加噪声$\varepsilon$,其分布为$q(\varepsilon)$,那么优化目标就变为
\begin{equation}\mathop{\text{argmin}}_{\theta} L_{\varepsilon}(\theta)=\mathbb{E}_{(x,y)\sim \mathcal{D}, \varepsilon\sim q(\varepsilon)}[l(f(x + \varepsilon), y)]\end{equation}
当然,可以添加噪声的地方不仅仅是输入,也可以是中间层,也可以是权重$\theta$,甚至可以是输出$y$(等价于标签平滑),噪声也不一定是加上去的,比如Dropout是乘上去的。对于加性噪声来说,$q(\varepsilon)$的常见选择是均值为0、方差固定的高斯分布;而对于乘性噪声来说,常见选择是均匀分布$U([0,1])$或者是伯努利分布。
添加随机噪声的目的很直观,就是希望模型能学会抵御一些随机扰动,从而降低对输入或者参数的敏感性,而降低了这种敏感性,通常意味着所得到的模型不再那么依赖训练集,所以有助于提高模型泛化性能。
为什么梯度裁剪能加速训练过程?一个简明的分析
By 苏剑林 | 2020-06-05 | 32323位读者 | 引用本文介绍来自MIT的一篇ICLR 2020满分论文《Why gradient clipping accelerates training: A theoretical justification for adaptivity》,顾名思义,这篇论文就是分析为什么梯度裁剪能加速深度学习的训练过程。原文很长,公式很多,还有不少研究复杂性的概念,说实话对笔者来说里边的大部分内容也是懵的,不过大概能捕捉到它的核心思想:引入了比常用的L约束更宽松的约束条件,从新的条件出发论证了梯度裁剪的必要性。本文就是来简明分析一下这个过程,供读者参考。
梯度裁剪
假设需要最小化的函数为$f(\theta)$,$\theta$就是优化参数,那么梯度下降的更新公式就是
\begin{equation}\theta \leftarrow \theta-\eta \nabla_{\theta} f(\theta)\end{equation}
其中$\eta$就是学习率。而所谓梯度裁剪(gradient clipping),就是根据梯度的模长来对更新量做一个缩放,比如
\begin{equation}\theta \leftarrow \theta- \eta \nabla_{\theta} f(\theta)\times \min\left\{1, \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert}\right\}\label{eq:clip-1}\end{equation}
或者
\begin{equation}\theta \leftarrow \theta- \eta \nabla_{\theta} f(\theta)\times \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert+\gamma}\label{eq:clip-2}\end{equation}
其中$\gamma > 0$是一个常数。这两种方式都被视为梯度裁剪,总的来说就是控制更新量的模长不超过一个常数,第二种形式也跟RMSProp等自适应学习率优化器相关。此外,更精确地,我们有下面的不等式
\begin{equation}\frac{1}{2}\min\left\{1, \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert}\right\}\leq \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert+\gamma}\leq \min\left\{1, \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert}\right\}\end{equation}
也就是说两者是可以相互控制的,所以其实两者基本是等价的。
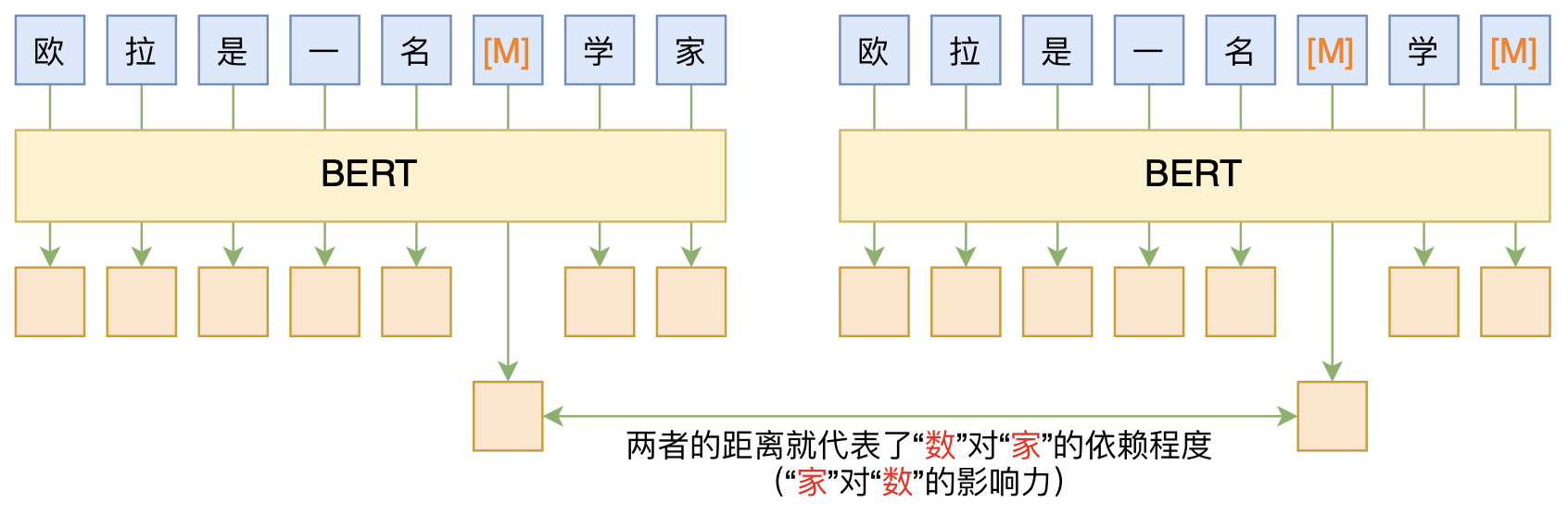
无监督分词和句法分析!原来BERT还可以这样用
By 苏剑林 | 2020-06-10 | 83122位读者 | 引用BERT的一般用法就是加载其预训练权重,再接一小部分新层,然后在下游任务上进行finetune,换句话说一般的用法都是有监督训练的。基于这个流程,我们可以做中文的分词、NER甚至句法分析,这些想必大家就算没做过也会有所听闻。但如果说直接从预训练的BERT(不finetune)就可以对句子进行分词,甚至析出其句法结构出来,那应该会让人感觉到意外和有趣了。
本文介绍ACL 2020的论文《Perturbed Masking: Parameter-free Probing for Analyzing and Interpreting BERT》,里边提供了直接利用Masked Language Model(MLM)来分析和解释BERT的思路,而利用这种思路,我们可以无监督地做到分词甚至句法分析。









最近评论