无监督分词和句法分析！原来BERT还可以这样用

BERT的一般用法就是加载其预训练权重，再接一小部分新层，然后在下游任务上进行finetune，换句话说一般的用法都是有监督训练的。基于这个流程，我们可以做中文的分词、NER甚至句法分析，这些想必大家就算没做过也会有所听闻。但如果说直接从预训练的BERT（不finetune）就可以对句子进行分词，甚至析出其句法结构出来，那应该会让人感觉到意外和有趣了。

本文介绍ACL 2020的论文《Perturbed Masking: Parameter-free Probing for Analyzing and Interpreting BERT》，里边提供了直接利用Masked Language Model（MLM）来分析和解释BERT的思路，而利用这种思路，我们可以无监督地做到分词甚至句法分析。

相关矩阵 #

本文建议配合如下文章来读：《【中文分词系列】 2. 基于切分的新词发现》、《最小熵原理（二）：“当机立断”之词库构建》、《最小熵原理（三）：“飞象过河”之句模版和语言结构》。这几篇文章主要是介绍了做无监督分词和句法分析的关键思想：相关矩阵。

token - token #

依照原文的记号，设待分析句子可以表示为token组成的序列$\boldsymbol{x}=[x_1,x_2,\dots,x_T]$，那么我们需要一个$T\times T$的相关矩阵$\mathcal{F}$，表示该句子中任意两个token的相关性。在上面推荐的那几篇文章中，我们用互信息来衡量这种相关性，而借助预训练好的BERT模型，我们可以提出新的相关性。

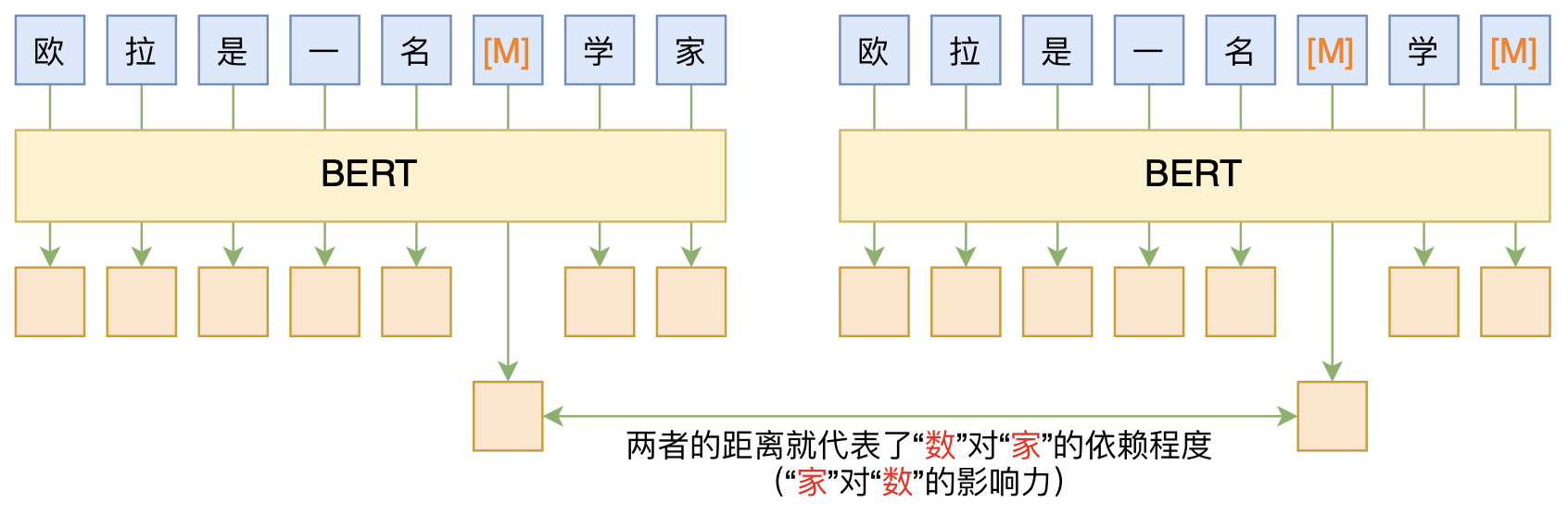
我们用$H(\boldsymbol{x})$表示序列$\boldsymbol{x}$经过BERT编码器后的输出序列，而$H(\boldsymbol{x})_i$则表示第$i$个token所对应的编码向量，另外，$\boldsymbol{x}\backslash \{x_i\}$表示将第$i$个token替换为$\text{[MASK]}$后的序列，$\boldsymbol{x}\backslash \{x_i,x_j\}$表示将第$i,j$个token都替换为$\text{[MASK]}$后的序列。设$f(x_i, x_j)$表示第$i$个token对第$j$个token的依赖程度，或者说第$j$个token对第$i$个token的“影响力”，那么我们将其定义为
\begin{equation}f(x_i, x_j)=d\big(H(\boldsymbol{x}\backslash \{x_i\})_i, H(\boldsymbol{x}\backslash \{x_i, x_j\})_i\big)\end{equation}
其中$d(\cdot,\cdot)$是某种向量距离，原论文用欧氏距离，即$d(\boldsymbol{u},\boldsymbol{v})=\Vert \boldsymbol{u} - \boldsymbol{v}\Vert_2$。

该定义的思路大概是：在MLM模型中，$H(\boldsymbol{x}\backslash \{x_i\})_i, H(\boldsymbol{x}\backslash \{x_i, x_j\})_i$都是用来预测$x_i$的特征，按照“mask越多、预测越不准“直观想法，我们有理由相信$H(\boldsymbol{x}\backslash \{x_i\})_i$比$H(\boldsymbol{x}\backslash \{x_i, x_j\})_i$能更准确地预测$x_i$，而$H(\boldsymbol{x}\backslash \{x_i, x_j\})_i$跟$H(\boldsymbol{x}\backslash \{x_i\})_i$相比就是去掉了$x_j$的信息，所以可以用两者的距离代表着$x_j$对$x_i$的“影响力”。

注1：原论文还提供了另一种定义$f(x_i,x_j)$的方式，但是语焉不详，并且笔者也觉得那种方式不够合理，因此这里也不介绍另一种方式了。

注2：可能读者会想到直接用BERT里边的Self Attention的注意力矩阵来作为相关性，但其实并不好：一来，BERT有那么多层，每层都有注意力矩阵，你也不知道哪个好；二来，文章《Google新作Synthesizer：我们还不够了解自注意力》告诉我们，注意力矩阵也许并不像我们想象中的那样工作，它里边的值也并不一定是相关性。

span - span #

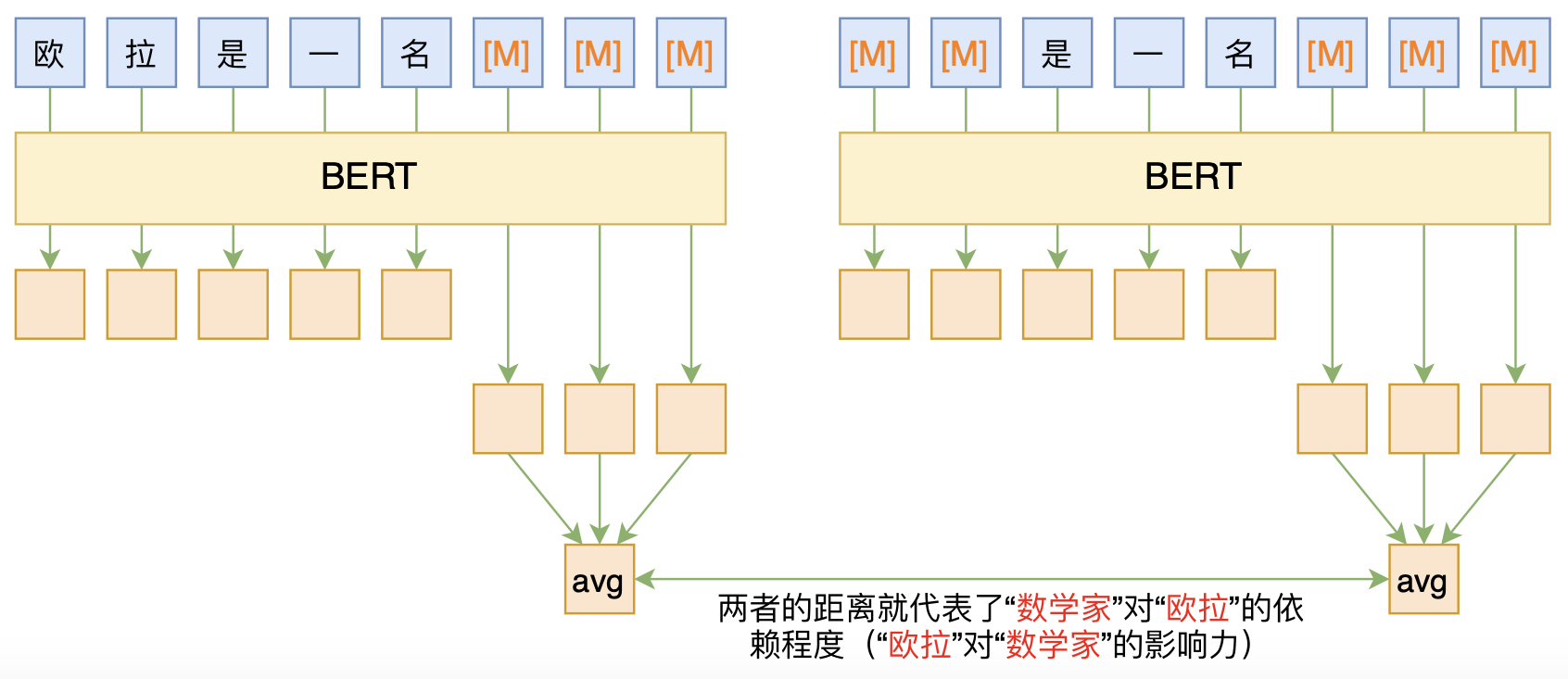
当然，我们并不一定要以token为单位，比如在句法分析中我们通常是以词为单位的，当然，BERT的输入还是token，所以我们需要将token分组成若干个span，即$D=[e_1,e_2,\dots,e_N]$，而$e_i=[x_1^i,x_2^i,\dots,x_{M_i}^i]$，这时候我们需要一个$N\times N$的相关矩阵，定义原理跟前面类似：
\begin{equation}f(e_i, e_j)=d\big(H(D\backslash \{e_i\})_i, H(D\backslash \{e_i, e_j\})_i\big)\end{equation}
这里$H(D\backslash \{e_i\})_i$是指BERT输出的$e_i$对应的$M_i$个向量的平均。

语言结构 #

有了这个相关矩阵之后，我们就可以做很多事情了，比如分词、句法分析等。一方面，BERT的MLM模型提供了一种无监督分词甚至句法分析的思路，另一方面，这些合理的无监督结果也反过来诠释了BERT本身的合理性，所以原论文的作者们才以“Analyzing and Interpreting BERT”为标题。

中文分词 #

作为一个基本的验证，我们可以试着用它来做无监督中文分词。这部分内容是笔者自己实验的，并没有出现在原论文中，大概是因为原论文的实验都是英文数据，而分词是相对来说是比较具有“中文特色”的任务吧。

事实上，有了相关矩阵之后，分词是一个很自然的应用。类似《【中文分词系列】 2. 基于切分的新词发现》和《最小熵原理（二）：“当机立断”之词库构建》，我们只需要考虑相邻token的相关性，设定一个阈值，然后把相关度小于这个阈值的两个token切开，大于等于这个阈值的两个token拼接，就构成了一个简单的分词工具了。在实验中，笔者用$\frac{f(x_i, x_{i+1}) + f(x_{i+1}, x_i)}{2}$作为相邻两个token的相关程度度量。

具体细节可以参考代码perturbed_masking/word_segment.py，下面是效果演示：

[u'习近平', u'总书记', u'6月', u'8日', u'赴', u'宁夏', u'考察', u'调研', u'。', u'当天', u'下午', u'，他先后', u'来到', u'吴忠', u'市', u'红寺堡镇', u'弘德', u'村', u'、黄河', u'吴忠', u'市城区段、', u'金星', u'镇金花园', u'社区', u'，', u'了解', u'当地', u'推进', u'脱贫', u'攻坚', u'、', u'加强', u'黄河流域', u'生态', u'保护', u'、', u'促进', u'民族团结', u'等', u'情况', u'。']

[u'大肠杆菌', u'是', u'人和', u'许多', u'动物', u'肠道', u'中最', u'主要', u'且数量', u'最多', u'的', u'一种', u'细菌']

[u'苏剑林', u'是', u'科学', u'空间', u'的博主']

[u'九寨沟', u'国家级', u'自然', u'保护', u'区', u'位于', u'四川', u'省', u'阿坝藏族羌族', u'自治', u'州', u'南坪县境内', u'，', u'距离', u'成都市400多公里', u'，', u'是', u'一条', u'纵深', u'40余公里', u'的山沟谷', u'地']

可以看到，效果还是相当赞的，虽然仍有点错漏，但是作为一个无监督的分词算法来说，已经是相当难得了。我们可以通过修改阈值进一步控制分词粒度，也可以将它作为一个分词发现工具来进一步提升分词效果（即将分词结果统计起来，然后过滤掉低频词，将剩下的词作为词库，来构建一个基于词库的分词工具）。值得说明的是，上述实验笔者用的是最早Google开源的BERT base版本，这个版本是没有融入分词信息的（后来的WWM版本是利用分词构建MASK，所以是融入了分词信息），所以上述分词效果确实算是纯无监督的。

句法分析 #

有相关背景的读者应该知道，跟分词类似，其实在有了相关矩阵之后，句法分析其实也是一件水到渠成的事情罢了。当然，由于这里的句法分析是无监督的，所以它只能想办法析出句子的层次结构（句法树）出来，无法像有监督的句法分析一样，贴上人为定义的句法结构标签。

同《ON-LSTM：用有序神经元表达层次结构》这篇论文一样，无监督句法分析的基本思路就是递归地将$\boldsymbol{x}=[x_1,x_2,\dots,x_T]$划分为$((\boldsymbol{x}_{ < k}),(x_k, (\boldsymbol{x}_{ > k})))$三部分（如果用span为单位，那么就将$x_i$改为$e_i$，步骤一样，不赘述）。这有点像聚类，其中$\boldsymbol{x}_{ < k}$是一类，而$\boldsymbol{x}_{\geq k}$是一类，聚类的思路也很普通，就是希望同类之间的相关性尽可能大，异类之间的相关性尽可能小，所以可以提出如下简单目标：
$$\begin{equation}\mathop{\text{argmax}}_k \underbrace{\frac{\sum\limits_{i=1}^{k-1}\sum\limits_{j=1}^{k-1} f(x_i, x_j)}{(k-1)^2}}_{\text{类内相关性}} + \underbrace{\frac{\sum\limits_{i=k}^{T}\sum\limits_{j=k}^{T} f(x_i, x_j)}{(T-k+1)^2}}_{\text{类内相关性}} - \underbrace{\frac{\sum\limits_{i=1}^{k-1}\sum\limits_{j=k}^{T} f(x_i, x_j)}{(k-1)(T-k+1)}}_{\text{类间相关性}} - \underbrace{\frac{\sum\limits_{i=k}^{T}\sum\limits_{j=1}^{k-1} f(x_i, x_j)}{(k-1)(T-k+1)}}_{\text{类间相关性}}\end{equation}$$
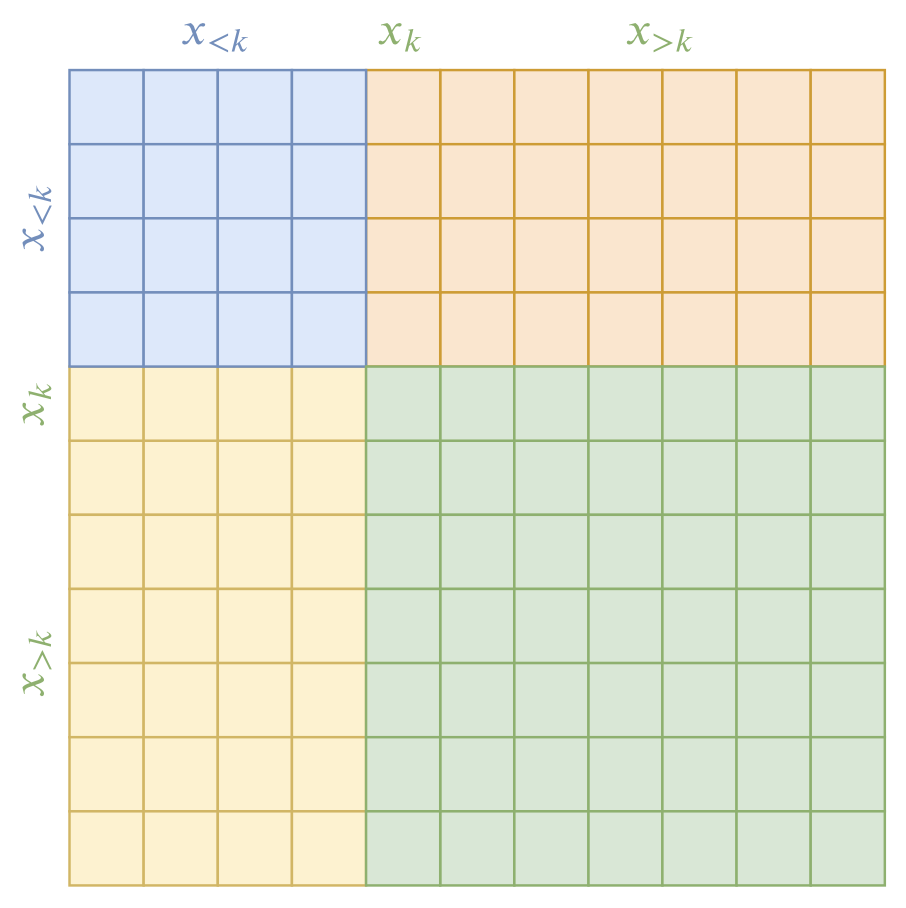
其中$f(x_i, x_i)$直接定义为0即可，这点细节不大重要，毕竟无监督的本来也不可能做得太精细。上面的公式看起来复杂，但事实上用一张图就可以表达清楚：

如图为距离矩阵的可视化，而聚类的目的，就是希望“蓝色部分和绿色部分的均值尽可能大，而黄色部分和橙色部分的均值尽可能小”，所以就有了上述公式的优化目标。

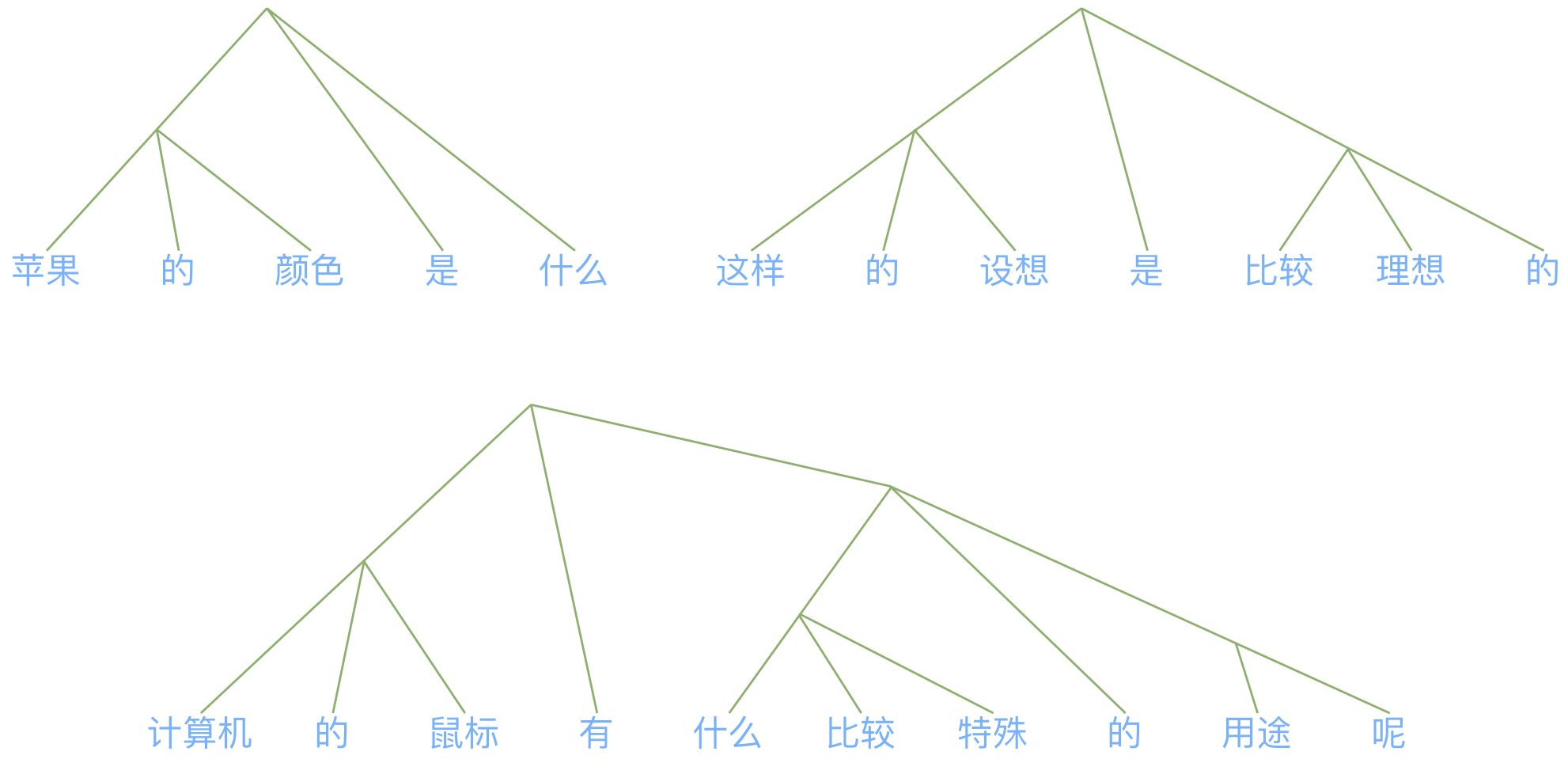
效果怎样呢？我们来试几个句子（事先分好词的，以词为单位构建）：

感觉确实基本析出了句子的层次结构。实现请参考代码：perturbed_masking/syntax_parsing.py。最后，原论文作者也开源了自己的代码（致敬开源），读者也可以参考阅读。

文章小结 #

本文简要介绍了ACL 2020的一篇论文，里边提出了基于BERT的MLM模型来对句子成分进行相关度计算的思路，利用算出来相关度，我们可以进行无监督的分词乃至句法分析，笔者利用bert4keras尝试在中文上复现了一下，证实了该思路的有效性。

转载到请包括本文地址：https://spaces.ac.cn/archives/7476

更详细的转载事宜请参考：《科学空间FAQ》