从EMD、WMD到WRD：文本向量序列的相似度计算

在NLP中，我们经常要去比较两个句子的相似度，其标准方法是想办法将句子编码为固定大小的向量，然后用某种几何距离（欧氏距离、$\cos$距离等）作为相似度。这种方案相对来说比较简单，而且检索起来比较快速，一定程度上能满足工程需求。

此外，还可以直接比较两个变长序列的差异性，比如编辑距离，它通过动态规划找出两个字符串之间的最优映射，然后算不匹配程度；现在我们还有Word2Vec、BERT等工具，可以将文本序列转换为对应的向量序列，所以也可以直接比较这两个向量序列的差异，而不是先将向量序列弄成单个向量。

后一种方案速度相对慢一点，但可以比较得更精细一些，并且理论比较优雅，所以也有一定的应用场景。本文就来简单介绍一下属于后者的两个相似度指标，分别简称为WMD、WRD。

Earth Mover's Distance #

本文要介绍的两个指标都是以Wasserstein距离为基础，这里会先对它做一个简单的介绍，相关内容也可以阅读笔者旧作《从Wasserstein距离、对偶理论到WGAN》。Wasserstein距离也被形象地称之为“推土机距离”（Earth Mover's Distance，EMD），因为它可以用一个“推土”的例子来通俗地表达它的含义。

最优传输 #

假设在位置$i=1,2,\dots,n$处我们分布有$p_1,p_2,\dots,p_n$那么多的土，简单起见我们设土的总数量为1，即$p_1 + p_2 + \dots + p_n=1$，现在要将土推到位置$j=1,2,\dots,n'$上，每处的量为$q_1, q_2, \dots, q_{n'}$，而从$i$推到$j$的成本为$d_{i,j}$，求成本最低的方案以及对应的最低成本。

这其实就是一个经典的最优传输问题。我们将最优方案表示为$\gamma_{i,j}$，表示这个方案中要从$i$中把$\gamma_{i,j}$数量的土推到$j$处，很明显我们有约束
\begin{equation}\sum_j \gamma_{i,j}=p_i,\quad \sum_i \gamma_{i,j}=q_j,\quad \gamma_{i,j} \geq 0\label{eq:cond}\end{equation}
所以我们的优化问题是
\begin{equation}\min_{\gamma_{i,j} \geq 0} \sum_{i,j} \gamma_{i,j} d_{i,j}\quad \text{s.t.} \quad \sum_j \gamma_{i,j}=p_i,\sum_i \gamma_{i,j}=q_j\end{equation}

参考实现 #

看上去复杂，但认真观察下就能发现上式其实就是一个线性规划问题——在线性约束下求线性函数的极值。而scipy就自带了线性规划求解函数linprog，因此我们可以利用它实现求Wasserstein距离的函数：

import numpy as np
from scipy.optimize import linprog

def wasserstein_distance(p, q, D):
    """通过线性规划求Wasserstein距离
    p.shape=[m], q.shape=[n], D.shape=[m, n]
    p.sum()=1, q.sum()=1, p∈[0,1], q∈[0,1]
    """
    A_eq = []
    for i in range(len(p)):
        A = np.zeros_like(D)
        A[i, :] = 1
        A_eq.append(A.reshape(-1))
    for i in range(len(q)):
        A = np.zeros_like(D)
        A[:, i] = 1
        A_eq.append(A.reshape(-1))
    A_eq = np.array(A_eq)
    b_eq = np.concatenate([p, q])
    D = D.reshape(-1)
    result = linprog(D, A_eq=A_eq[:-1], b_eq=b_eq[:-1])
    return result.fun

读者可以留意到，在传入约束的时候用的是A_eq=A_eq[:-1], b_eq=b_eq[:-1]，也就是去掉了最后一个约束。这是因为$1=\sum\limits_{i=1}^n p_i = \sum\limits_{j=1}^{n'} q_j$，所以$\eqref{eq:cond}$中的等式约束本身存在冗余，而实际计算中有时候可能存在浮点误差，导致冗余的约束之间相互矛盾，从而使得线性规划的求解失败，所以干脆去掉最后一个冗余的约束，减少出错的可能性。

Word Mover's Distance #

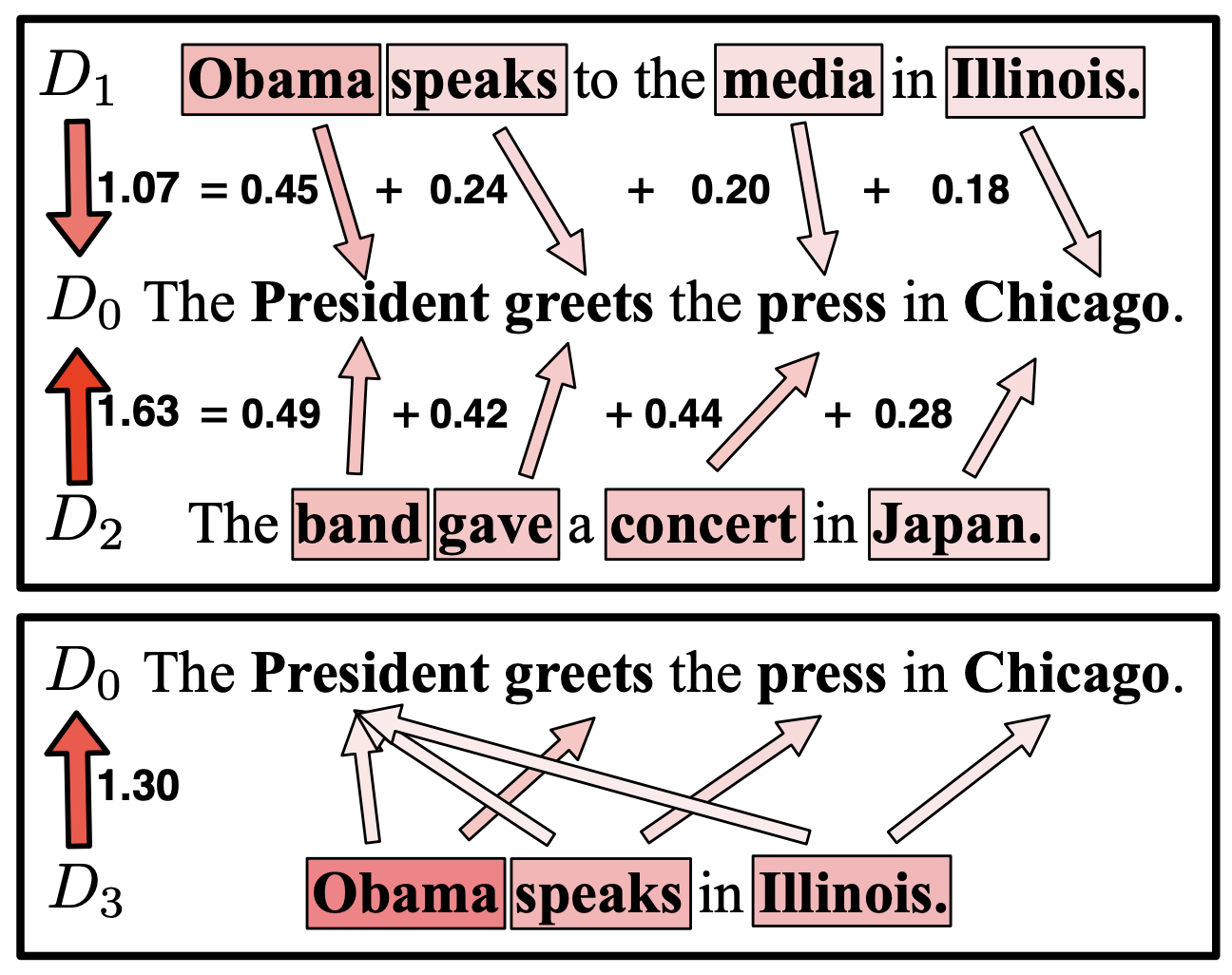
很明显，Wasserstein距离适合于用来计算两个不同长度的序列的差异性，而我们要做语义相似度的时候，两个句子通常也是不同长度的，刚好对应这个特性，因此很自然地就会联想到Wasserstein距离也许可以用来比较句子相似度，而首次进行这个尝试的是论文《From Word Embeddings To Document Distances》。

基本形式 #

设有两个句子$s = (t_1,t_2,\dots,t_n), s' = (t'_1, t'_2, \dots, t'_{n'})$，经过某种映射（比如Word2Vec或者BERT）后，它们变成了对应的向量序列$(\boldsymbol{w}_1,\boldsymbol{w}_2,\dots,\boldsymbol{w}_n), (\boldsymbol{w}'_1, \boldsymbol{w}'_2, \dots, \boldsymbol{w}'_{n'})$，现在我们就想办法用Wasserstein距离来比较这两个序列的相似度。

根据前一节的介绍，Wasserstein距离需要知道$p_i,q_j,d_{i,j}$三个量，我们逐一把它们都定义好即可。由于没有什么先验知识，所以我们可以很朴素地将让$p_i\equiv \frac{1}{n}, q_j\equiv \frac{1}{n'}$，所以现在还剩$d_{i,j}$。显然，$d_{i,j}$代表着第一个序列的向量$\boldsymbol{w}_i$与第二个序列的向量$\boldsymbol{w}'_j$的某种差异性，简单起见我们可以用欧氏距离$\left\Vert \boldsymbol{w}_i - \boldsymbol{w}'_j\right\Vert$，所以两个句子的差异程度可以表示为
\begin{equation}\min_{\gamma_{i,j} \geq 0} \sum_{i,j} \gamma_{i,j} \left\Vert \boldsymbol{w}_i - \boldsymbol{w}'_j\right\Vert\quad \text{s.t.} \quad \sum_j \gamma_{i,j}=\frac{1}{n},\sum_i \gamma_{i,j}=\frac{1}{n'}\end{equation}
这便是Word Mover's Distance（WMD）（推词机距离？？），大概可以理解为将一个句子变为另一个句子的最短路径，某种意义上也可以理解为编辑距离的光滑版。实际使用的时候，通常会去掉停用词后再计算WMD。

参考实现 #

参考实现如下：

def word_mover_distance(x, y):
    """WMD（Word Mover's Distance）的参考实现
    x.shape=[m,d], y.shape=[n,d]
    """
    p = np.ones(x.shape[0]) / x.shape[0]
    q = np.ones(y.shape[0]) / y.shape[0]
    D = np.sqrt(np.square(x[:, None] - y[None, :]).mean(axis=2))
    return wasserstein_distance(p, q, D)

下界公式 #

如果是检索场景，要将输入句子跟数据库里边所有句子一一算WMD并排序的话，那计算成本是相当大的，所以我们要尽量减少算WMD的次数，比如通过一些更简单高效的指标来过滤掉一些样本，然后才对剩下的样本算WMD。

幸运的是，我们确实可以推导出WMD的一个下界公式，原论文称之为Word Centroid Distance（WCD）：
\begin{equation}\begin{aligned}
\sum_{i,j} \gamma_{i,j} \left\Vert \boldsymbol{w}_i - \boldsymbol{w}'_j\right\Vert =& \sum_{i,j} \left\Vert \gamma_{i,j}(\boldsymbol{w}_i - \boldsymbol{w}'_j)\right\Vert\\
\geq& \left\Vert \sum_{i,j}\gamma_{i,j}(\boldsymbol{w}_i - \boldsymbol{w}'_j)\right\Vert\\
=& \left\Vert \sum_i\left(\sum_j\gamma_{i,j}\right)\boldsymbol{w}_i - \sum_j\left(\sum_i\gamma_{i,j}\right)\boldsymbol{w}'_j\right\Vert\\
=& \left\Vert \frac{1}{n}\sum_i\boldsymbol{w}_i - \frac{1}{n'}\sum_j\boldsymbol{w}'_j\right\Vert\\
\end{aligned}\end{equation}
也就是说，WMD大于两个句子的平均向量的欧氏距离，所以我们要检索WMD比较小的句子时，可以先用WCD把距离比较大的句子先过滤掉，然后剩下的采用WMD比较。

Word Rotator's Distance #

WMD其实已经挺不错了，但非要鸡蛋里挑骨头的话，还是能挑出一些缺点来：

1、它使用的是欧氏距离作为语义差距度量，但从Word2Vec的经验我们就知道要算词向量的相似度的话，用$\cos$往往比欧氏距离要好；

2、WMD理论上是一个无上界的量，这意味着我们不大好直观感知相似程度，从而不能很好调整相似与否的阈值。

为了解决这两个问题，一个比较朴素的想法是将所有向量除以各自的模长来归一化后再算WMD，但这样就完全失去了模长信息了。最近的论文《Word Rotator's Distance: Decomposing Vectors Gives Better Representations》则巧妙地提出，在归一化的同时可以把模长融入到约束条件$p,q$里边去，这就形成了WRD。

基本形式 #

首先，WRD提出了“词向量的模长正相关于这个词的重要程度”的观点，并通过一些实验结果验证了这个观点。事实上，这个观点跟笔者之前提出的simpler glove模型的观点一致，参考《更别致的词向量模型(五)：有趣的结果》。而在WMD中，$p_i,q_j$某种意义上也代表着对应句子中某个词的重要程度，所以我们可以设
\begin{equation}\begin{aligned}&p_i = \frac{\left\Vert \boldsymbol{w}_i\right\Vert}{Z}, &Z=\sum_{i=1}^n \left\Vert\boldsymbol{w}_i\right\Vert\\
&q_j = \frac{\left\Vert \boldsymbol{w}'_j\right\Vert}{Z'}, &Z'=\sum_{j=1}^{n'}\left\Vert\boldsymbol{w}'_j\right\Vert
\end{aligned}\end{equation}
然后$d_{i,j}$就用余弦距离：
\begin{equation}d_{i,j}=1 - \frac{\boldsymbol{w}_i\cdot \boldsymbol{w}'_j}{\left\Vert\boldsymbol{w}_i\right\Vert\times \left\Vert\boldsymbol{w}'_j\right\Vert}\end{equation}
得到
\begin{equation}\min_{\gamma_{i,j} \geq 0} \sum_{i,j} \gamma_{i,j} \left(1 - \frac{\boldsymbol{w}_i\cdot \boldsymbol{w}'_j}{\left\Vert\boldsymbol{w}_i\right\Vert\times \left\Vert\boldsymbol{w}'_j\right\Vert}\right)\quad \text{s.t.} \quad \sum_j \gamma_{i,j}=\frac{\left\Vert \boldsymbol{w}_i\right\Vert}{Z},\sum_i \gamma_{i,j}=\frac{\left\Vert \boldsymbol{w}'_j\right\Vert}{Z'}\end{equation}
这就是Word Rotator's Distance（WRD）了。由于使用的度量是余弦距离，所以两个向量之间的变换更像是一种旋转（rotate）而不是移动（move），所以有了这个命名；同样由于使用了余弦距离，所以它的结果在$[0,2]$内，相对来说更容易去感知其相似程度。

参考实现 #

参考实现如下：

def word_rotator_distance(x, y):
    """WRD（Word Rotator's Distance）的参考实现
    x.shape=[m,d], y.shape=[n,d]
    """
    x_norm = (x**2).sum(axis=1, keepdims=True)**0.5
    y_norm = (y**2).sum(axis=1, keepdims=True)**0.5
    p = x_norm[:, 0] / x_norm.sum()
    q = y_norm[:, 0] / y_norm.sum()
    D = 1 - np.dot(x / x_norm, (y / y_norm).T)
    return wasserstein_distance(p, q, D)


def word_rotator_similarity(x, y):
    """1 - WRD
    x.shape=[m,d], y.shape=[n,d]
    """
    return 1 - word_rotator_distance(x, y)

下界公式 #

同WMD一样，我们也可以推导出WRD的一个下界公式：
\begin{equation}\begin{aligned}
2\sum_{i,j} \gamma_{i,j} \left(1 - \frac{\boldsymbol{w}_i\cdot \boldsymbol{w}'_j}{\left\Vert\boldsymbol{w}_i\right\Vert\times \left\Vert\boldsymbol{w}'_j\right\Vert}\right)=&\sum_{i,j} \gamma_{i,j} \left\Vert \frac{\boldsymbol{w}_i}{\left\Vert \boldsymbol{w}_i\right\Vert} - \frac{\boldsymbol{w}'_j}{\left\Vert \boldsymbol{w}'_j\right\Vert}\right\Vert^2 \\
\geq& \left\Vert \sum_{i,j}\gamma_{i,j}\left(\frac{\boldsymbol{w}_i}{\left\Vert \boldsymbol{w}_i\right\Vert} - \frac{\boldsymbol{w}'_j}{\left\Vert \boldsymbol{w}'_j\right\Vert}\right)\right\Vert^2\\
=& \left\Vert \sum_i\left(\sum_j\gamma_{i,j}\right)\frac{\boldsymbol{w}_i}{\left\Vert \boldsymbol{w}_i\right\Vert} - \sum_j\left(\sum_i\gamma_{i,j}\right)\frac{\boldsymbol{w}'_j}{\left\Vert \boldsymbol{w}'_j\right\Vert}\right\Vert^2\\
=& \left\Vert \frac{1}{Z}\sum_i\boldsymbol{w}_i - \frac{1}{Z'}\sum_j\boldsymbol{w}'_j\right\Vert^2\\
\end{aligned}\end{equation}
其中不等号基于詹森不等式（或者基本不等式的推广版）。不过这部分内容并没有出现在WRD的论文中，只是笔者自行补充的。

又到了文末小结的时候 #

文本介绍了两种文本相似度算法WMD、WRD，它们都是利用Wasserstein距离（Earth Mover's Distance，推土机距离）来直接比较两个不定长向量的差异性。这类相似度算法在效率上会有所欠缺，但是理论上比较优雅，而且效果也颇为不错，值得学习一番。

转载到请包括本文地址：https://spaces.ac.cn/archives/7388

更详细的转载事宜请参考：《科学空间FAQ》