你见过正方形轮子的自行车吗?一般认为,只有圆形的车轮才能使我们的车子平稳向前移动,但这只是针对平直道路而言的。谁规定路一定是平的?只要铺好一条适当的道路,正方形车轮的自行车照样可以平稳前行!本文就让我们为方轮自行车铺一条路。
其实,方轮自行车已经不是新鲜玩意了,它早已出现在不少科技馆中。从图片中可以看到,它的特殊轨道是有许多段弧组成的,每一段弧的长度等于正方形的边长。车轮前行时,正方形会保持与弧形相切(确保不会打滑)。这样的路的形状是什么曲线呢?很幸运,它并不十分复杂,而且让人意外的是,它就是我们之前已经研究过的“悬链线”!原来,要设计这样的一个曲线的轨道,不需要多么高深的设计师,只需要我们手拿一条铁链,让它自由垂下......
费曼积分法——积分符号内取微分(4)
By 苏剑林 | 2012-06-26 | 72127位读者 | 引用趁着早上有空,就赶紧把这篇文章写好吧。下午高考成绩要公布了,公布后也许又会有一段时间忙碌了。这应该是“费曼积分法”系列最后一篇文章了。它主要讲的还是费曼积分法的一个实例。不同的是,这是BoJone首次独立地用费曼积分法解决了一个问题。之前提到的一些例子,都是书本提供并结合了提示,BoJone才把它们算出来的。所以这个问题有着点点纪念意义。
数学研发论坛上wayne曾求证这样的命题:
$\int_0^{\infty}\frac{f(x,2m-1)-\sin x}{x^{2m+1}}dx$其中,f(x,2m-1)表示sinx的2m-1阶泰勒展开
如m=1时,
$$\int_0^{\infty}\frac{x-\sin x}{x^3}dx$$
m=2时
$$\int_0^{\infty}\frac{x-\frac{x^3}{6}-\sin x}{x^5}dx$$
借助软件我发现结果是:
$\frac{\pi(-1)^{m-1}}{2(2m)!}$
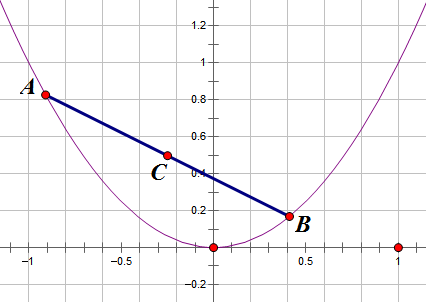
抛物线内一根定长的弦
By 苏剑林 | 2012-06-30 | 32344位读者 | 引用今天傍晚看到了彩虹!当然这算不上什么奇观,但还是一道美丽的风景。
人说“不经历风雨,怎么见彩虹”,我发现彩虹不一定是在雨后的,今天我看彩虹的时候,就是暴风雨前夕。彩虹是在18点10分左右出现的,持续了5分钟左右吧,看着看着,雨越下越大,我被迫停止欣赏了,不过彩虹也随之消失了。
用一个老相机简单记录了一下这道亮丽的风景!这是我第一次拍摄彩虹^_^
不知道是相机问题还是真有其事,在照片上发现有两条彩虹。难道这次的彩虹是”双彩虹“?那可真是奇观了!

很老的家用数码相机,没有广角,不能拍摄全景,这是用photoshop把两张图片拼凑起来的,效果不好
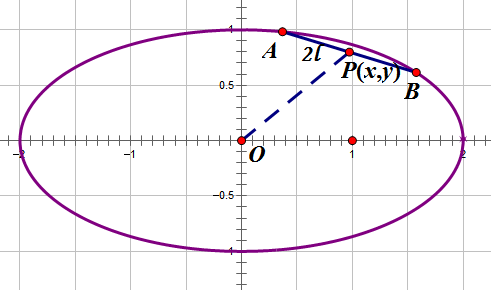
椭圆内的一根定长弦(化圆法)
By 苏剑林 | 2012-07-06 | 30702位读者 | 引用在上一篇文章《抛物线内的一根定长弦》中,我们解决了抛物线内的定长弦中点轨迹问题,那还算是一个比较简单的问题。虽然同是圆锥曲线,但把同样的问题延伸到椭圆上,却不是那么简单了。因为椭圆的轨迹方程的x,y坐标通过平方相互“纠缠”在一起,不像抛物线方程那样可以容易分离开来(指的是分离成$y=f(x)$的形式)。BoJone尝试了若干种方法,还是难以把它的轨迹求出来。最后通过“化圆法”,终得轨迹方程。
所谓化圆法,就是将椭圆通过拉伸变成一个圆,利用圆的性质来解决一些问题。众所周知,相比椭圆,圆具有相当多的简单性。这是我高考前研究各种各样的高考圆锥曲线题时,所总结出来的一种方法。有时候,把椭圆拉伸为圆后,结论就相当显然了;同时,圆作为一个特殊的椭圆,椭圆的一般结论,放在圆上自然也是成立的。所以要研究椭圆问题,不妨先研究它的特例——圆问题;另一方面,利用圆的对称性等等,也可以大幅度地减少计算量,所以BoJone很喜欢这个方法。更想不到的是,它居然在求本文的轨迹时派上用场了。
昨天清晨,台风“韦森特”正式来袭我们新兴,话说凌晨三点我已经被风声吵醒了。大概7点钟起床,刚好是台风最抢镜的时候,猛烈地刮呀刮,声音有点像卡车启动的声音......
昨天一整天断电,上午还断了固定电话(农村地区是这样的啦,断电是整体的,台风刮倒了电线杆;断电话是我自己家的问题),中午的时候,固话却自动连上了,郁闷中。下午风雨都基本停下来了,妈妈和我们就出去收拾“残局”,被风刮倒的东西可真不少,尤其是我家门口的两个小棚,惨不忍睹;还有门前的一些盆栽、菜、树等,都倒下了不少。三个人爬上爬下,慢慢维修、收拾。
晚上还是没来电,也好,很久没有尝试过烛光晚餐了。九点多钟的时候,电来了,但是又是一番故障——其他人家中的电都很正常,就我这里灯泡很暗、日光灯启动不了,明显是电压不够的问题。没办法,只好硬着头皮抢修了,排除了很多原因,最后甚至从隔壁家搭电过来,发现我们家的灯还是那么暗(电压不足的问题没有解决)——这说明只有一个可能了,外部电路都没有故障,是我家的内部电路出了问题,猜想某个地方串联了一个用电器分去了电压。但是电线都镶进墙里了,这么黑根本维修不了,没办法,先睡觉了。
复分析学习1:揭示微分与积分的联系
By 苏剑林 | 2012-08-02 | 34463位读者 | 引用笔者这段时间对复数尤其感兴趣,当然,严格来讲应该是复变函数内容,其中一个原因是通过它,我们可以把一些看似毫不相关的内容联系了起来,体现了数学的简洁美和统一美。我相当有兴趣的其中一个内容是实分析中的泰勒级数和傅里叶级数。这两者都是关于某个函数的级数展开式,其中泰勒级数是用于一般函数展开的,其各项系数通过求n阶导数得到;傅里叶级数的对象是周期函数,其各项系数是通过定积分求得的。在实数世界里,两者毫不相关,但是,复分析却告诉我们:它们只是同一个东西!只是将其在不同的角度“投影”到实数世界里,就产生了不同的“物像”,以至于我们认为它们是不同东西而已。
我们直接来看一个变魔术般的运算:
我们知道,在实数世界里头,我们有
$ln(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+...$,其中$|x| < 1$
站长注:这篇文章来源于网络,原文是繁体中文版本,我经过修改整理而成。它原来是《费曼的6堂Easy物理课》这本书的解说,但是由于内容上的详细和扼要,我更愿意把它当做物理学家费曼的解说,与大家分享。
伟哉!费曼
社会上普遍有种错误的想法,总以为科学是完全客观的,不但不会因人而异,更不会感情用事。对比之下,科学以外的各种人类活动,则多多少少会受到一般潮流动向、突发的时尚风潮,以及当事人的性格、偏好所左右。唯有科学,得受制于科学社群都同意的规则、步骤,与严密的测试、检验。科学仅着重于得到的结论,而不在乎谁是做研究、做实验的人。
以上说法显然是无稽之谈,科学既然靠人推动,就跟其他人类活动相同,都会受到大环境趋势及个人意念的影响。在科学领域,研究潮流的趋向受到主题素材选择的影响并不大,却相当取决于当时科学家对整个世界的看法。









最近评论