椭圆内的一根定长弦（化圆法）

在上一篇文章《抛物线内的一根定长弦》中，我们解决了抛物线内的定长弦中点轨迹问题，那还算是一个比较简单的问题。虽然同是圆锥曲线，但把同样的问题延伸到椭圆上，却不是那么简单了。因为椭圆的轨迹方程的x,y坐标通过平方相互“纠缠”在一起，不像抛物线方程那样可以容易分离开来（指的是分离成$y=f(x)$的形式）。BoJone尝试了若干种方法，还是难以把它的轨迹求出来。最后通过“化圆法”，终得轨迹方程。

所谓化圆法，就是将椭圆通过拉伸变成一个圆，利用圆的性质来解决一些问题。众所周知，相比椭圆，圆具有相当多的简单性。这是我高考前研究各种各样的高考圆锥曲线题时，所总结出来的一种方法。有时候，把椭圆拉伸为圆后，结论就相当显然了；同时，圆作为一个特殊的椭圆，椭圆的一般结论，放在圆上自然也是成立的。所以要研究椭圆问题，不妨先研究它的特例——圆问题；另一方面，利用圆的对称性等等，也可以大幅度地减少计算量，所以BoJone很喜欢这个方法。更想不到的是，它居然在求本文的轨迹时派上用场了。

如何把椭圆化为圆呢？很简单，设椭圆的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$，只需要把椭圆的y轴坐标拉伸为原来的$\frac{a}{b}$倍，椭圆就变成了$x^2+y^2=a^2$；或者把椭圆的x轴左边收缩为原来的$\frac{b}{a}$，椭圆就变成了$x^2+y^2=b^2$。

拉伸或收缩后的图形有什么特点呢？原来的相交、相切、相离关系保持不变，图形面积按长度伸缩的比例进行变化（只伸缩了一维，所以不用平方），当然角度和长度都会变化等等，在下面的计算中读者能够体验到具体过程。

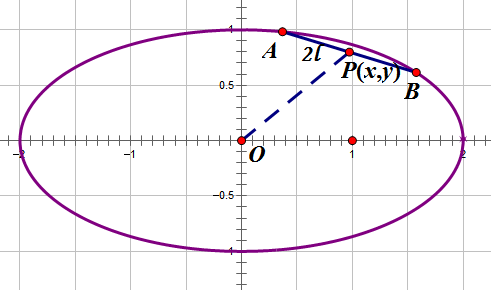
如图，椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$内有定长弦AB，$|AB|=2l$，其中P(x,y)是AB的中点，设AB的斜率为k。

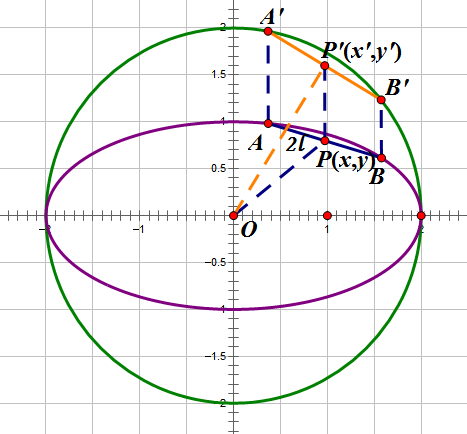
采用拉伸的方法，将椭圆的y轴坐标拉伸为原来的$\frac{a}{b}$倍，得到结果如下：

P点变成了$P'(x',y')=P'(x,\frac{a}{b}y)$
斜率k变成了$k'=\frac{a}{b}k$

那么长度怎么变化呢？我们有弦长公式$|AB|=\sqrt{1+k^2}|x_A-x_B|$，可见弦长正比于$\sqrt{1+k^2}$，所以拉伸后的弦长为

$$|A'B'|=2l\cdot \sqrt{\frac{1+\frac{a^2}{b^2}k^2}{1+k^2}}$$

容易得到OP'的斜率为：$\frac{y'}{x'}=\frac{ay}{bx}=-\frac{1}{k'}=-\frac{b}{ak}$

从中解得$k=-\frac{b^2 x}{a^2 y}$

我们也可以求出OP'的长度了。

$$|OP'|^2=x'^2+y'^2=x^2+\frac{a^2}{b^2}y^2$$

另一方面，它也等于

$$a^2-(\frac{|A'B'|}{2})^2=a^2-l^2(\frac{1+\frac{a^2}{b^2}k^2}{1+k^2})$$

即

$$x^2+\frac{a^2}{b^2}y^2=a^2-(\frac{|A'B'|}{2})^2=a^2-l^2(\frac{1+\frac{a^2}{b^2}k^2}{1+k^2})$$

根据我们得出的$k=-\frac{b^2 x}{a^2 y}$，代入上式并经过一系列化简后可以得到

$$a^2 b^2[1-l^2(\frac{a^2 y^2+b^2 x^2}{a^4 y^2+b^4 x^2})]=a^2 y^2+b^2 x^2$$

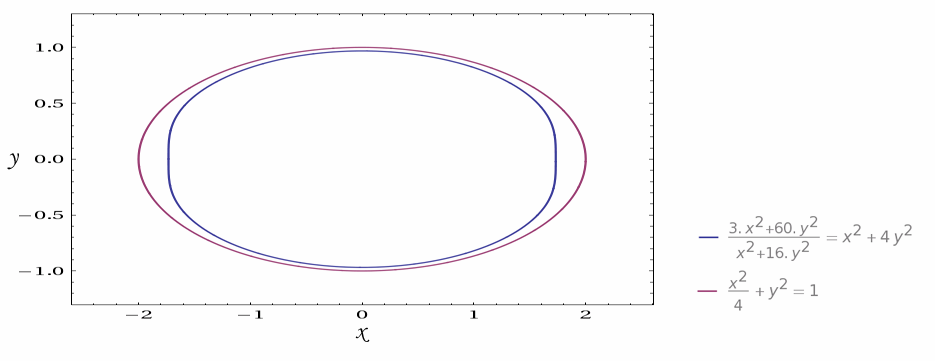
这就是轨迹方程！当然，也可以经过化简变成下面的结果。在我看来，下面的式子更好看些：
$$\sqrt{a^2 b^2-a^2 y^2-b^2 x^2}\cdot \sqrt{\frac{a^4 y^2+b^4 x^2}{a^2 y^2+b^2 x^2}}=lab$$
（本结果获于2012.06.05）

这是a=2,b=1,l=0.5时的结果：

总结

“化圆法”是一种几何变换的方法，是应对圆锥曲线的练习题的大计算量的一种有效方法。当然，它有它的局限性。尤其是遇到定角问题时这个方法往往都会失效了，具体情况需要读者在实际应用中多多摸索总结。高中的学习过程中，老师们为了统一，几乎都不会讲述这个技巧。但是它却由于它的通用性和简洁性深为我喜欢。虽然有点“偏方”的味道，但实在是很多应用。有兴趣的朋友以后遇到相关题目时，不妨多从这个角度思考一下，或许会有意外的收获。另一方面，其实很多在圆中相当简单的几何结论（如切割线定理），通过伸缩变换成椭圆，就会成为一道相当不错的圆锥曲线练习题。这也可能是圆锥曲线题目命题者的一个出题思路。

转载到请包括本文地址：https://spaces.ac.cn/archives/1654

更详细的转载事宜请参考：《科学空间FAQ》