《向量》系列——2.曲率半径

圆周是如此地和谐与完美，致使数学家和物理学家对它钟爱有加。几何上可以把一条曲线的局部看做一个圆弧，利用圆的性质去研究它（在数学上，曲率半径的倒数就是曲率，曲率越大，曲线越弯曲）；物理学家喜欢把一个质点的曲线运动轨迹的局部看做圆周运动，利用圆周运动的方法来描述这种运动。这两种研究方法都告诉了我们，两种不同的“线”在极小的范围内可以等效的，这也为我们对科学进行探究提供了一点指导思想：把未知变已知，以已知看未知。物理学和数学的两种处理方法中，有一点是殊途同归的：那就是看轨迹看成一个圆后，圆的半径是多少？我们首先得求出它。

在数学分析上可以利用微积分的相关知识来推导曲率半径公式，而BoJone则更偏爱物理方法，通过物理和向量知识的结合，推导出曲率半径公式，让BoJone感到“别有一番风味”。

推导1：

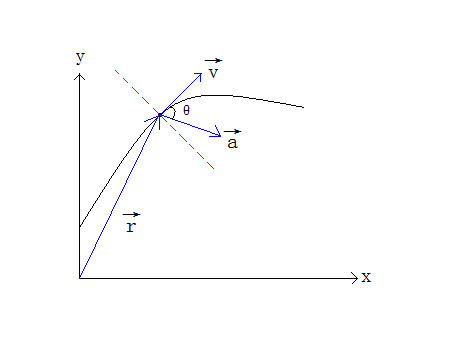
首先来考虑二维的情况。我们知道向心加速度公式为$a_c=\frac{v^2}{R}$，如果我们可以知道向心加速度和速度，就可以求出R(曲率半径)。对于任意给出一个运动方程$\vec{r}=\vec{r}(t)$，那么速度我们已经知道了，$\vec{v}=\dot{\vec{r}}$。剩下的未知量是向心加速度。

何为“向心”？其实就是加速度在该点所在的圆的半径的投影。我们知道，圆周运动的速度方向总是与半径方向垂直，所以“向心”的方向其实就是与速度垂直的方向（这也叫做“法(线)向”，所以向心加速度也叫“法向加速度”）。

$$\vec{a}=\ddot{\vec{r}},|a_c|=|\vec{a}|\cdot \sin\theta=|\dot{\vec{r}}\times \ddot{\vec{r}}|\div |\dot{\vec{r}}|$$

因此$R=\frac{v^2}{a_c}=\frac{|\dot{\vec{r}}|^3}{|\dot{\vec{r}}\times \ddot{\vec{r}}|}$

令$\vec{r}=(x,y,0)$，则有
$$\begin{aligned}\dot{\vec{r}}=(\dot{x},\dot{y},0),\ddot{\vec{r}}=(\ddot{x},\ddot{y},0) \\ \dot{\vec{r}}\times \ddot{\vec{r}}=(0,0,\dot{x}\ddot{y}-\dot{y}\ddot{x})\end{aligned}$$

代入有：$R=\frac{(\dot{x}^2+\dot{y}^2)^(3//2)}{|\dot{x}\ddot{y}-\dot{y}\ddot{x}|}$
如果采取三维坐标代入，可以得到三维空间曲线的曲率半径：
$$R=\frac{(x'^2+y'^2+z'^2)^{3//2}}{\sqrt{(z''y'-y''z')^2+(x''z'-z''x')^2+(y''x'-x''y')^2}}$$

推导2：
在这里我们得到了关于圆周运动的两条方程
$$\vec{R}\cdot \dot{\vec{r}}=0\tag{1}$$$$\dot{\vec{r}}^2+\vec{R}\cdot \ddot{\vec{r}}=0\tag{2}$$
同样令$\vec{r}=(x,y),\vec{R}=(a,b)$，代入得到
$$\dot{x}^2+\dot{y}^2+a\ddot{x}+b\ddot{y}=0;a\dot{x}+b\dot{y}=0$$

可以解出
$$\begin{aligned}a=-\frac{\dot{x}^2\dot{y}+\dot{y}^3}{\ddot{x}\dot{y}-\dot{x}\ddot{y}} \\ b=\frac{\dot{y}^2\dot{x}+\dot{x}^3}{\ddot{x}\dot{y}-\dot{x}\ddot{y}}\end{aligned}$$
$R=\sqrt{a^2+b^2}=\frac{(\dot{x}^2+\dot{y}^2)^(3//2)}{|\dot{x}\ddot{y}-\dot{y}\ddot{x}|}$

转载到请包括本文地址：https://spaces.ac.cn/archives/714

更详细的转载事宜请参考：《科学空间FAQ》