科学空间|Scientific Spaces

由于自行车之旅的原因，这篇文章被搁置了一个星期，其实应该在一个星期前就把它写好的。这篇文章继续讲讲费曼积分法的一些例子。读者或许可以从这些不同类型的例子中，发现它应用的基本方向和方法，从而提升对它的认识。

例子2：

$$\int_0^{\infty} \frac{\sin x}{x}dx$$

这也是一种比较常见的类型，它的形式为$\int \frac{f(x)}{x}dx$，对于这种形式，我们的第一感觉就是将其改写成参数形式$\int \frac{f(ax)}{x}dx$，这样的目的很简单，就是把分母给消去了，与$\int \frac{x}{f(x)}dx$的求积思想是一致的。但是深入一点研究就会发现，纵使这样能够消去分母，使得第一次积分变得简单，但是到了第二次积分的时候，我们发现，它又会变回$\int \frac{f(x)}{x}dx$的积分，使我们不能继续进行下去，因此这个取参数的方法大多数情况下都是不行的。

点击阅读全文...

趁着早上有空，就赶紧把这篇文章写好吧。下午高考成绩要公布了，公布后也许又会有一段时间忙碌了。这应该是“费曼积分法”系列最后一篇文章了。它主要讲的还是费曼积分法的一个实例。不同的是，这是BoJone首次独立地用费曼积分法解决了一个问题。之前提到的一些例子，都是书本提供并结合了提示，BoJone才把它们算出来的。所以这个问题有着点点纪念意义。

数学研发论坛上wayne曾求证这样的命题：

$\int_0^{\infty}\frac{f(x,2m-1)-\sin x}{x^{2m+1}}dx$其中，f(x,2m-1)表示sinx的2m-1阶泰勒展开
如m=1时，
$$\int_0^{\infty}\frac{x-\sin x}{x^3}dx$$
m=2时
$$\int_0^{\infty}\frac{x-\frac{x^3}{6}-\sin x}{x^5}dx$$
借助软件我发现结果是：
$\frac{\pi(-1)^{m-1}}{2(2m)!}$

点击阅读全文...

今天傍晚看到了彩虹！当然这算不上什么奇观，但还是一道美丽的风景。

人说“不经历风雨，怎么见彩虹”，我发现彩虹不一定是在雨后的，今天我看彩虹的时候，就是暴风雨前夕。彩虹是在18点10分左右出现的，持续了5分钟左右吧，看着看着，雨越下越大，我被迫停止欣赏了，不过彩虹也随之消失了。

用一个老相机简单记录了一下这道亮丽的风景！这是我第一次拍摄彩虹^_^

不知道是相机问题还是真有其事，在照片上发现有两条彩虹。难道这次的彩虹是”双彩虹“？那可真是奇观了！

很老的家用数码相机，没有广角，不能拍摄全景，这是用photoshop把两张图片拼凑起来的，效果不好

点击阅读全文...

如图是一个三角形，要求三角形的外角和。外角和定义为“多边形每一个内角的补角之和”，比如这里的∠DAC+∠FCB+∠EBA。当然，这里一般指的是凸多边形。

三角形的外角和 (1)

显然，这并不是一个什么大难题，答案是360度，方法有很多，直接用内角和公式计算、想象成旋转一周甚至你亲自去测量一下都行。但我觉得最妙的方法无疑是下面的方法。

点击阅读全文...

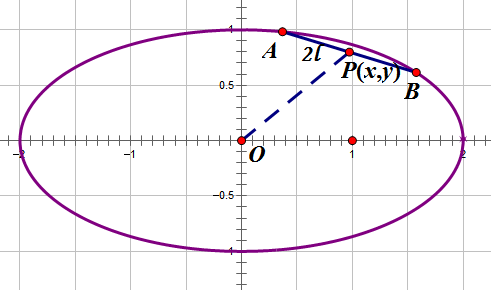
在上一篇文章《抛物线内的一根定长弦》中，我们解决了抛物线内的定长弦中点轨迹问题，那还算是一个比较简单的问题。虽然同是圆锥曲线，但把同样的问题延伸到椭圆上，却不是那么简单了。因为椭圆的轨迹方程的x,y坐标通过平方相互“纠缠”在一起，不像抛物线方程那样可以容易分离开来（指的是分离成$y=f(x)$的形式）。BoJone尝试了若干种方法，还是难以把它的轨迹求出来。最后通过“化圆法”，终得轨迹方程。

椭圆内的定长弦1

所谓化圆法，就是将椭圆通过拉伸变成一个圆，利用圆的性质来解决一些问题。众所周知，相比椭圆，圆具有相当多的简单性。这是我高考前研究各种各样的高考圆锥曲线题时，所总结出来的一种方法。有时候，把椭圆拉伸为圆后，结论就相当显然了；同时，圆作为一个特殊的椭圆，椭圆的一般结论，放在圆上自然也是成立的。所以要研究椭圆问题，不妨先研究它的特例——圆问题；另一方面，利用圆的对称性等等，也可以大幅度地减少计算量，所以BoJone很喜欢这个方法。更想不到的是，它居然在求本文的轨迹时派上用场了。

点击阅读全文...

经过10天的抢险维修，数据中心机房开始逐步恢复运行。科学空间也能够正常访问了！激动中...^_^

这是科学空间建立以来，宇宙驿站服务器所经受的最大一次灾难了，中断时间是迄今为止最长的一次。大量的天文科普网站都被中断，原因很简单，它们和科学空间一样，都把网站寄放在宇宙驿站服务器上。除了科学空间，中断访问的还有牧夫天文论坛、星友空间站、空间天文网等等。

点击阅读全文...

计算机模拟的希格斯粒子（“上帝粒子”）衰变

笔者：对于科学界来说，七月份最重大的事情莫过于在LHC我们终于发现了希格斯玻色子的踪迹。BoJone到《新科学家》网站上选取了一篇文章进行翻译，让大家了解其中的一些事情。当然，发现这个希格斯玻色子已经是七月四号的事情了，现在已经是非常迟到了，中间的原因就是宇宙驿站的故障了......迟到总比没到好，现在发出来，与大家共勉。翻译得不好，请指出毛病，高手见笑了^_^

庆祝希格斯玻色子的最终发现！

作者：日内瓦的CERN 的Celeste Biever 2012年7月4日

点击阅读全文...

分类：千奇百怪,物理化学 标签：翻译, 模型, 粒子, 玻色子 阅读全文 3 评论

宇宙驿站维修期间，BoJone曾经想过用自己的电脑来搭建服务器，建立一个临时页面。但后来发现经常开着电脑不大好，就没有这样做了。不过如何在自己的电脑上搭建服务器，还是值得笔记一下的。

BoJone还在使用WinXP专业版系统，最标准的方法当然是使用IIS，可以一气呵成。但是考虑到IIS需要配置挺多东西的，所以就没有这样做了。所以自己在网上下载一些小软件，“拼凑”成了一个临时服务器。这样的方法也能够很方便地应用到各个Windows系统。

点击阅读全文...