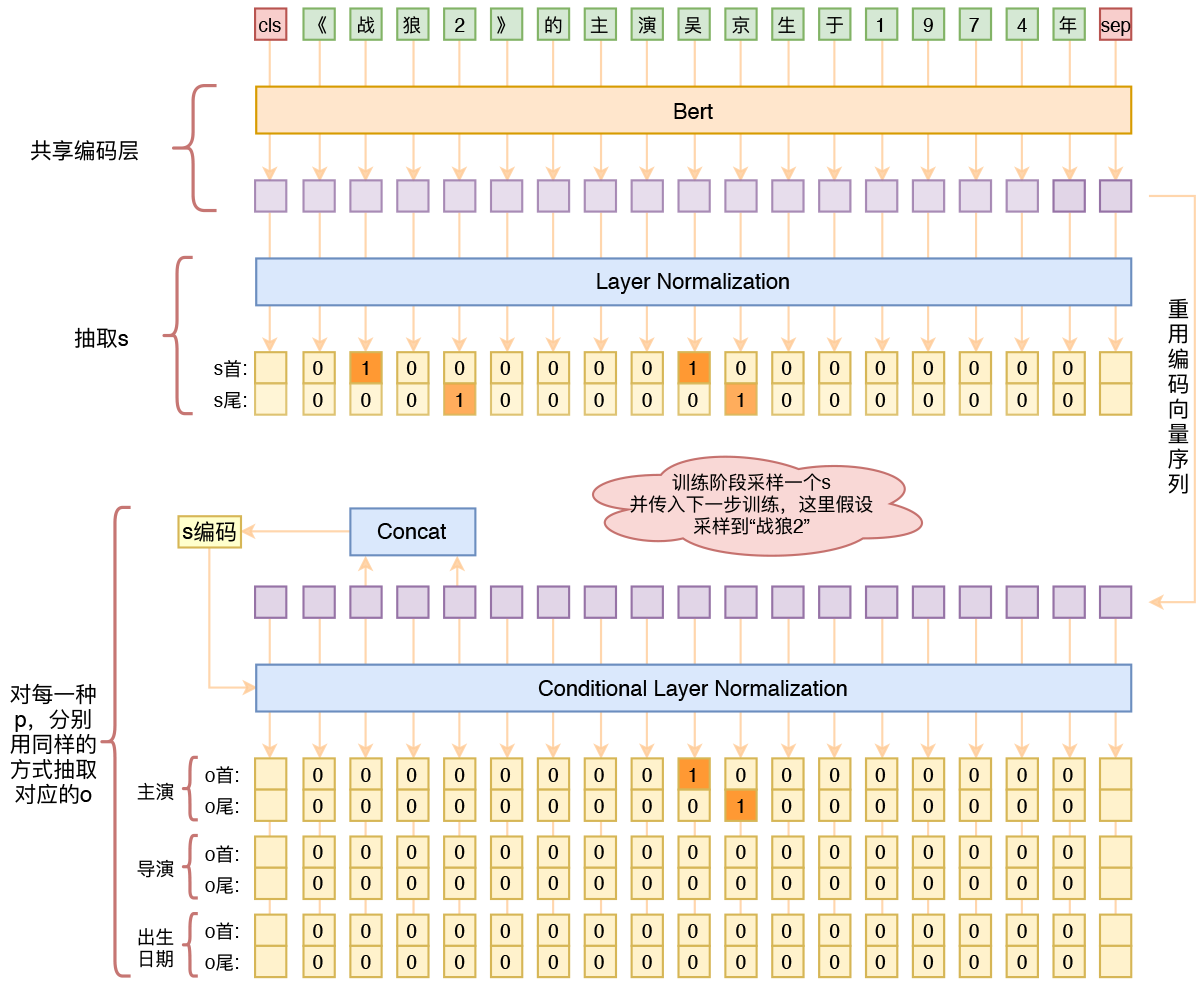
用bert4keras做三元组抽取
By 苏剑林 | 2020-01-03 | 255619位读者 | 引用在开发bert4keras的时候就承诺过,会逐渐将之前用keras-bert实现的例子逐渐迁移到bert4keras来,而那里其中一个例子便是三元组抽取的任务。现在bert4keras的例子已经颇为丰富了,但还没有序列标注和信息抽取相关的任务,而三元组抽取正好是这样的一个任务,因此就补充上去了。
基于DGCNN和概率图的轻量级信息抽取模型
By 苏剑林 | 2019-06-03 | 409792位读者 | 引用背景:前几个月,百度举办了“2019语言与智能技术竞赛”,其中有三个赛道,而我对其中的“信息抽取”赛道颇感兴趣,于是报名参加。经过两个多月的煎熬,比赛终于结束,并且最终结果已经公布。笔者从最初的对信息抽取的一无所知,经过这次比赛的学习和研究,最终探索出在监督学习下做信息抽取的一些经验,遂在此与大家分享。
笔者在最终的测试集上排名第七,指标F1为0.8807(Precision是0.8939,Recall是0.8679),跟第一名相差0.01左右。从比赛角度这个成绩不算突出,但自认为模型有若干创新之处,比如自行设计的抽取结构、CNN+Attention(所以足够快速)、没有用Bert等预训练模型,私以为这对于信息抽取的学术研究和工程应用都有一定的参考价值。
基本分析
信息抽取(Information Extraction, IE)是从自然语言文本中抽取实体、属性、关系及事件等事实类信息的文本处理技术,是信息检索、智能问答、智能对话等人工智能应用的重要基础,一直受到业界的广泛关注。... 本次竞赛将提供业界规模最大的基于schema的中文信息抽取数据集(Schema based Knowledge Extraction, SKE),旨在为研究者提供学术交流平台,进一步提升中文信息抽取技术的研究水平,推动相关人工智能应用的发展。------ 比赛官方网站介绍
漫谈重参数:从正态分布到Gumbel Softmax
By 苏剑林 | 2019-06-10 | 229103位读者 | 引用最近在用VAE处理一些文本问题的时候遇到了对离散形式的后验分布求期望的问题,于是沿着“离散分布 + 重参数”这个思路一直搜索下去,最后搜到了Gumbel Softmax,从对Gumbel Softmax的学习过程中,把重参数的相关内容都捋了一遍,还学到一些梯度估计的新知识,遂记录在此。
文章从连续情形出发开始介绍重参数,主要的例子是正态分布的重参数;然后引入离散分布的重参数,这就涉及到了Gumbel Softmax,包括Gumbel Softmax的一些证明和讨论;最后再讲讲重参数背后的一些故事,这主要跟梯度估计有关。
基本概念
重参数(Reparameterization)实际上是处理如下期望形式的目标函数的一种技巧:
\begin{equation}L_{\theta}=\mathbb{E}_{z\sim p_{\theta}(z)}[f(z)]\label{eq:base}\end{equation}
这样的目标在VAE中会出现,在文本GAN也会出现,在强化学习中也会出现($f(z)$对应于奖励函数),所以深究下去,我们会经常碰到这样的目标函数。取决于$z$的连续性,它对应不同的形式:
\begin{equation}\int p_{\theta}(z) f(z)dz\,\,\,\text{(连续情形)}\qquad\qquad \sum_{z} p_{\theta}(z) f(z)\,\,\,\text{(离散情形)}\end{equation}
当然,离散情况下我们更喜欢将记号$z$换成$y$或者$c$。
简述无偏估计和有偏估计
By 苏剑林 | 2019-06-19 | 81643位读者 | 引用对于大多数读者(包括笔者)来说,他们接触到的第一个有偏估计量,应该是方差
\begin{equation}\hat{\sigma}^2_{\text{有偏}} = \frac{1}{n}\sum_{i=1}^n \left(x_i - \hat{\mu}\right)^2,\quad \hat{\mu} = \frac{1}{n}\sum_{i=1}^n x_i\label{eq:youpianfangcha}\end{equation}
然后又了解到对应的无偏估计应该是
\begin{equation}\hat{\sigma}^2_{\text{无偏}} = \frac{1}{n-1}\sum_{i=1}^n \left(x_i - \hat{\mu}\right)^2\label{eq:wupianfangcha}\end{equation}
在很多人的眼里,公式$\eqref{eq:youpianfangcha}$才是合理的,怎么就有偏了?公式$\eqref{eq:wupianfangcha}$将$n$换成反直觉的$n-1$,反而就无偏了?
下面试图用尽量清晰的语言讨论一下无偏估计和有偏估计两个概念。
为节约而生:从标准Attention到稀疏Attention
By 苏剑林 | 2019-07-27 | 133724位读者 | 引用如今NLP领域,Attention大行其道,当然也不止NLP,在CV领域Attention也占有一席之地(Non Local、SAGAN等)。在18年初《〈Attention is All You Need〉浅读(简介+代码)》一文中,我们就已经讨论过Attention机制,Attention的核心在于$\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}$三个向量序列的交互和融合,其中$\boldsymbol{Q},\boldsymbol{K}$的交互给出了两两向量之间的某种相关度(权重),而最后的输出序列则是把$\boldsymbol{V}$按照权重求和得到的。
显然,众多NLP&CV的成果已经充分肯定了Attention的有效性。本文我们将会介绍Attention的一些变体,这些变体的共同特点是——“为节约而生”——既节约时间,也节约显存。
背景简述
《Attention is All You Need》一文讨论的我们称之为“乘性Attention”,目前用得比较广泛的也就是这种Attention:
\begin{equation}Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}) = softmax\left(\frac{\boldsymbol{Q}\boldsymbol{K}^{\top}}{\sqrt{d_k}}\right)\boldsymbol{V}\end{equation}
最小熵原理(五):“层层递进”之社区发现与聚类
By 苏剑林 | 2019-10-19 | 152645位读者 | 引用让我们不厌其烦地回顾一下:最小熵原理是一个无监督学习的原理,“熵”就是学习成本,而降低学习成本是我们的不懈追求,所以通过“最小化学习成本”就能够无监督地学习出很多符合我们认知的结果,这就是最小熵原理的基本理念。
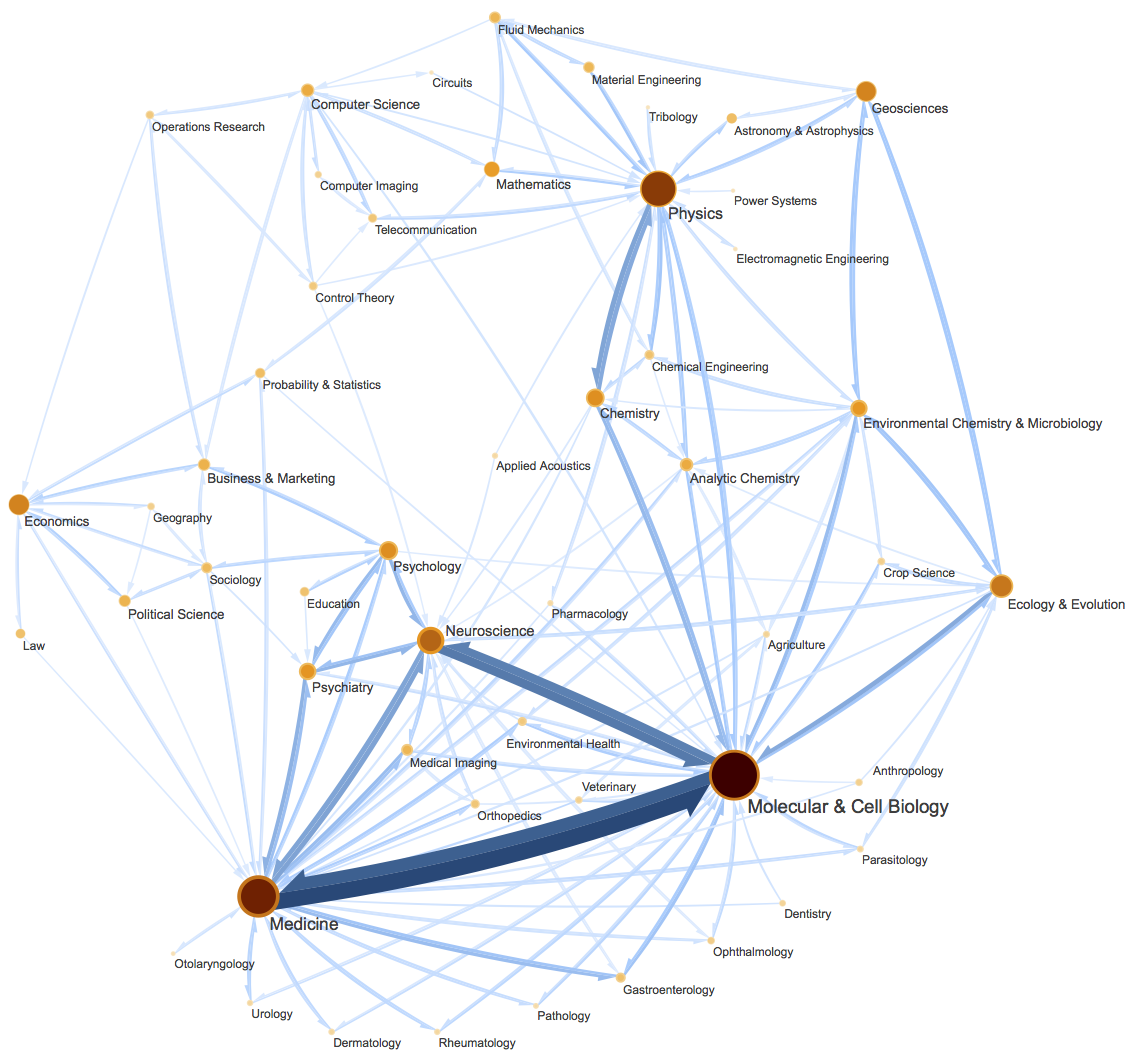
这篇文章里,我们会介绍一种相当漂亮的聚类算法,它同样也体现了最小熵原理,或者说它可以通过最小熵原理导出来,名为InfoMap,或者MapEquation。事实上InfoMap已经是2007年的成果了,最早的论文是《Maps of random walks on complex networks reveal community structure》,虽然看起来很旧,但我认为它仍是当前最漂亮的聚类算法,因为它不仅告诉了我们“怎么聚类”,更重要的是给了我们一个“为什么要聚类”的优雅的信息论解释,并从这个解释中直接导出了整个聚类过程。
当然,它的定位并不仅仅局限在聚类上,更准确地说,它是一种图网络上的“社区发现”算法。所谓社区发现(Community Detection),大概意思是给定一个有向/无向图网络,然后找出这个网络上的“抱团”情况,至于详细含义,大家可以自行搜索一下。简单来说,它跟聚类相似,但是比聚类的含义更丰富。(还可以参考《什么是社区发现?》)
“非自回归”也不差:基于MLM的阅读理解问答
By 苏剑林 | 2019-12-26 | 83498位读者 | 引用“让Keras更酷一些!”:层与模型的重用技巧
By 苏剑林 | 2019-09-29 | 108532位读者 | 引用今天我们继续来深挖Keras,再次体验Keras那无与伦比的优雅设计。这一次我们的焦点是“重用”,主要是层与模型的重复使用。
所谓重用,一般就是奔着两个目标去:一是为了共享权重,也就是说要两个层不仅作用一样,还要共享权重,同步更新;二是避免重写代码,比如我们已经搭建好了一个模型,然后我们想拆解这个模型,构建一些子模型等。
基础
事实上,Keras已经为我们考虑好了很多,所以很多情况下,掌握好基本用法,就已经能满足我们很多需求了。
层的重用
层的重用是最简单的,将层初始化好,存起来,然后反复调用即可:
x_in = Input(shape=(784,))
x = x_in
layer = Dense(784, activation='relu') # 初始化一个层,并存起来
x = layer(x) # 第一次调用
x = layer(x) # 再次调用
x = layer(x) # 再次调用








![用MLM做阅读理解的模型图示(其中[M]表示[MASK]标记)](/usr/uploads/2019/12/1024911876.png)

最近评论