《Attention is All You Need》浅读(简介+代码)
By 苏剑林 | 2018-01-06 | 1212743位读者 |2017年中,有两篇类似同时也是笔者非常欣赏的论文,分别是FaceBook的《Convolutional Sequence to Sequence Learning》和Google的《Attention is All You Need》,它们都算是Seq2Seq上的创新,本质上来说,都是抛弃了RNN结构来做Seq2Seq任务。
这篇博文中,笔者对《Attention is All You Need》做一点简单的分析。当然,这两篇论文本身就比较火,因此网上已经有很多解读了(不过很多解读都是直接翻译论文的,鲜有自己的理解),因此这里尽可能多自己的文字,尽量不重复网上各位大佬已经说过的内容。
序列编码 #
深度学习做NLP的方法,基本上都是先将句子分词,然后每个词转化为对应的词向量序列。这样一来,每个句子都对应的是一个矩阵$\boldsymbol{X}=(\boldsymbol{x}_1,\boldsymbol{x}_2,\dots,\boldsymbol{x}_t)$,其中$\boldsymbol{x}_i$都代表着第$i$个词的词向量(行向量),维度为$d$维,故$\boldsymbol{X}\in \mathbb{R}^{n\times d}$。这样的话,问题就变成了编码这些序列了。
第一个基本的思路是RNN层,RNN的方案很简单,递归式进行:
\begin{equation}\boldsymbol{y}_t = f(\boldsymbol{y}_{t-1},\boldsymbol{x}_t)\end{equation}
不管是已经被广泛使用的LSTM、GRU还是最近的SRU,都并未脱离这个递归框架。RNN结构本身比较简单,也很适合序列建模,但RNN的明显缺点之一就是无法并行,因此速度较慢,这是递归的天然缺陷。另外我个人觉得RNN无法很好地学习到全局的结构信息,因为它本质是一个马尔科夫决策过程。
第二个思路是CNN层,其实CNN的方案也是很自然的,窗口式遍历,比如尺寸为3的卷积,就是
\begin{equation}\boldsymbol{y}_t = f(\boldsymbol{x}_{t-1},\boldsymbol{x}_t,\boldsymbol{x}_{t+1})\end{equation}
在FaceBook的论文中,纯粹使用卷积也完成了Seq2Seq的学习,是卷积的一个精致且极致的使用案例,热衷卷积的读者必须得好好读读这篇文论。CNN方便并行,而且容易捕捉到一些全局的结构信息,笔者本身是比较偏爱CNN的,在目前的工作或竞赛模型中,我都已经尽量用CNN来代替已有的RNN模型了,并形成了自己的一套使用经验,这部分我们以后再谈。
Google的大作提供了第三个思路:纯Attention!单靠注意力就可以!RNN要逐步递归才能获得全局信息,因此一般要双向RNN才比较好;CNN事实上只能获取局部信息,是通过层叠来增大感受野;Attention的思路最为粗暴,它一步到位获取了全局信息!它的解决方案是:
\begin{equation}\boldsymbol{y}_t = f(\boldsymbol{x}_{t},\boldsymbol{A},\boldsymbol{B})\end{equation}
其中$\boldsymbol{A},\boldsymbol{B}$是另外一个序列(矩阵)。如果都取$\boldsymbol{A}=\boldsymbol{B}=\boldsymbol{X}$,那么就称为Self Attention,它的意思是直接将$\boldsymbol{x}_t$与原来的每个词进行比较,最后算出$\boldsymbol{y}_t$!
Attention层 #
Attention定义 #
Google的一般化Attention思路也是一个编码序列的方案,因此我们也可以认为它跟RNN、CNN一样,都是一个序列编码的层。
前面给出的是一般化的框架形式的描述,事实上Google给出的方案是很具体的。首先,它先把Attention的定义给了出来:
\begin{equation}Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}) = softmax\left(\frac{\boldsymbol{Q}\boldsymbol{K}^{\top}}{\sqrt{d_k}}\right)\boldsymbol{V}\end{equation}
这里用的是跟Google的论文一致的符号,其中$\boldsymbol{Q}\in\mathbb{R}^{n\times d_k}, \boldsymbol{K}\in\mathbb{R}^{m\times d_k}, \boldsymbol{V}\in\mathbb{R}^{m\times d_v}$。如果忽略激活函数$softmax$的话,那么事实上它就是三个$n\times d_k,d_k\times m, m\times d_v$的矩阵相乘,最后的结果就是一个$n\times d_v$的矩阵。于是我们可以认为:这是一个Attention层,将$n\times d_k$的序列$\boldsymbol{Q}$编码成了一个新的$n\times d_v$的序列。
那怎么理解这种结构呢?我们不妨逐个向量来看。
\begin{equation}Attention(\boldsymbol{q}_t,\boldsymbol{K},\boldsymbol{V}) = \sum_{s=1}^m \frac{1}{Z}\exp\left(\frac{\langle\boldsymbol{q}_t, \boldsymbol{k}_s\rangle}{\sqrt{d_k}}\right)\boldsymbol{v}_s\end{equation}
其中$Z$是归一化因子。事实上$q,k,v$分别是$query,key,value$的简写,$\boldsymbol{K},\boldsymbol{V}$是一一对应的,它们就像是key-value的关系,那么上式的意思就是通过$\boldsymbol{q}_t$这个query,通过与各个$\boldsymbol{k}_s$内积的并softmax的方式,来得到$\boldsymbol{q}_t$与各个$\boldsymbol{v}_s$的相似度,然后加权求和,得到一个$d_v$维的向量。其中因子$\sqrt{d_k}$起到调节作用,使得内积不至于太大(太大的话softmax后就非0即1了,不够“soft”了)。
事实上这种Attention的定义并不新鲜,但由于Google的影响力,我们可以认为现在是更加正式地提出了这个定义,并将其视为一个层地看待;此外这个定义只是注意力的一种形式,还有一些其他选择,比如$query$跟$key$的运算方式不一定是点乘(还可以是拼接后再内积一个参数向量),甚至权重都不一定要归一化,等等。
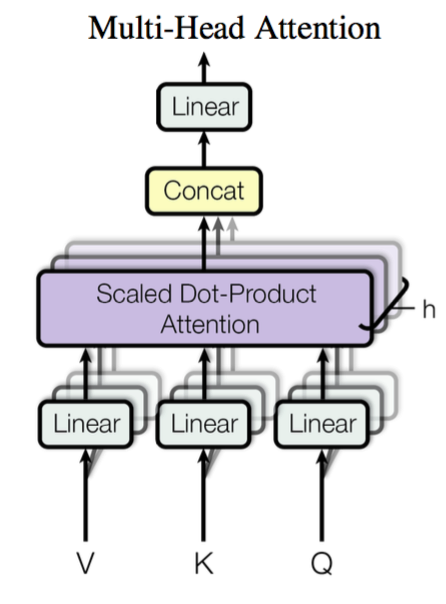
Multi-Head Attention #
这个是Google提出的新概念,是Attention机制的完善。不过从形式上看,它其实就再简单不过了,就是把$\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}$通过参数矩阵映射一下,然后再做Attention,把这个过程重复做$h$次,结果拼接起来就行了,可谓“大道至简”了。具体来说
\begin{equation}head_i = Attention(\boldsymbol{Q}\boldsymbol{W}_i^Q,\boldsymbol{K}\boldsymbol{W}_i^K,\boldsymbol{V}\boldsymbol{W}_i^V)\end{equation}
这里$\boldsymbol{W}_i^Q\in\mathbb{R}^{d_k\times \tilde{d}_k}, \boldsymbol{W}_i^K\in\mathbb{R}^{d_k\times \tilde{d}_k}, \boldsymbol{W}_i^V\in\mathbb{R}^{d_v\times \tilde{d}_v}$,然后
\begin{equation}MultiHead(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}) = Concat(head_1,...,head_h)\end{equation}
最后得到一个$n\times (h\tilde{d}_v)$的序列。所谓“多头”(Multi-Head),就是只多做几次同样的事情(参数不共享),然后把结果拼接。
Self Attention #
到目前为止,对Attention层的描述都是一般化的,我们可以落实一些应用。比如,如果做阅读理解的话,$\boldsymbol{Q}$可以是篇章的向量序列,取$\boldsymbol{K}=\boldsymbol{V}$为问题的向量序列,那么输出就是所谓的Aligned Question Embedding。
而在Google的论文中,大部分的Attention都是Self Attention,即“自注意力”,或者叫内部注意力。
所谓Self Attention,其实就是$Attention(\boldsymbol{X},\boldsymbol{X},\boldsymbol{X})$,$\boldsymbol{X}$就是前面说的输入序列。也就是说,在序列内部做Attention,寻找序列内部的联系。Google论文的主要贡献之一是它表明了内部注意力在机器翻译(甚至是一般的Seq2Seq任务)的序列编码上是相当重要的,而之前关于Seq2Seq的研究基本都只是把注意力机制用在解码端。类似的事情是,目前SQUAD阅读理解的榜首模型R-Net也加入了自注意力机制,这也使得它的模型有所提升。
当然,更准确来说,Google所用的是Self Multi-Head Attention:
\begin{equation}\boldsymbol{Y}=MultiHead(\boldsymbol{X},\boldsymbol{X},\boldsymbol{X})\end{equation}
Position Embedding #
然而,只要稍微思考一下就会发现,这样的模型并不能捕捉序列的顺序!换句话说,如果将$\boldsymbol{K},\boldsymbol{V}$按行打乱顺序(相当于句子中的词序打乱),那么Attention的结果还是一样的。这就表明了,到目前为止,Attention模型顶多是一个非常精妙的“词袋模型”而已。
这问题就比较严重了,大家知道,对于时间序列来说,尤其是对于NLP中的任务来说,顺序是很重要的信息,它代表着局部甚至是全局的结构,学习不到顺序信息,那么效果将会大打折扣(比如机器翻译中,有可能只把每个词都翻译出来了,但是不能组织成合理的句子)。
于是Google再祭出了一招——Position Embedding,也就是“位置向量”,将每个位置编号,然后每个编号对应一个向量,通过结合位置向量和词向量,就给每个词都引入了一定的位置信息,这样Attention就可以分辨出不同位置的词了。
Position Embedding并不算新鲜的玩意,在FaceBook的《Convolutional Sequence to Sequence Learning》也用到了这个东西。但在Google的这个作品中,它的Position Embedding有几点区别:
1、以前在RNN、CNN模型中其实都出现过Position Embedding,但在那些模型中,Position Embedding是锦上添花的辅助手段,也就是“有它会更好、没它也就差一点点”的情况,因为RNN、CNN本身就能捕捉到位置信息。但是在这个纯Attention模型中,Position Embedding是位置信息的唯一来源,因此它是模型的核心成分之一,并非仅仅是简单的辅助手段。
2、在以往的Position Embedding中,基本都是根据任务训练出来的向量。而Google直接给出了一个构造Position Embedding的公式:
\begin{equation}\left\{\begin{aligned}&PE_{2i}(p)=\sin\Big(p/10000^{2i/{d_{pos}}}\Big)\\
&PE_{2i+1}(p)=\cos\Big(p/10000^{2i/{d_{pos}}}\Big)
\end{aligned}\right.\end{equation}
这里的意思是将id为$p$的位置映射为一个$d_{pos}$维的位置向量,这个向量的第$i$个元素的数值就是$PE_i(p)$。Google在论文中说到他们比较过直接训练出来的位置向量和上述公式计算出来的位置向量,效果是接近的。因此显然我们更乐意使用公式构造的Position Embedding了,我们称之为Sinusoidal形式的Position Embedding。3、Position Embedding本身是一个绝对位置的信息,但在语言中,相对位置也很重要,Google选择前述的位置向量公式的一个重要原因是:由于我们有$\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$以及$\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$,这表明位置$p+k$的向量可以表示成位置$p$的向量的线性变换,这提供了表达相对位置信息的可能性。
结合位置向量和词向量有几个可选方案,可以把它们拼接起来作为一个新向量,也可以把位置向量定义为跟词向量一样大小,然后两者加起来。FaceBook的论文和Google论文中用的都是后者。直觉上相加会导致信息损失,似乎不可取,但Google的成果说明相加也是很好的方案。看来我理解还不够深刻。
还有,尽管论文给出的Position Embedding是$\sin,\cos$交错的形式,但其实这个交错形式没有特别的意义,你可以按照任意的方式重排它(比如前$\sin$后$\cos$地拼接),原因如下:
1、假如你的Position_Embedding是拼接到原来的词向量中,那么将$\cos$和$\sin$前后连接还是交叉连接,都是没区别的,因为你下一步都是接一个变换矩阵而已;
2、如果你的Position_Embedding是加到原来的词向量中,那么两种方式貌似是有点区别的,但是要注意的是,词向量本身没有局部结构,也就是说,50维的词向量,将每一维打乱重新排个序(当然整体要按同样的顺序来重新排序),它还是等价于原来的词向量。既然相加的对象(词向量)都没有局部结构,我们也没必要强调被加的对象(Position_Embedding)的局部结构(也就是交叉连接)了。
一些不足之处 #
到这里,Attention机制已经基本介绍完了。Attention层的好处是能够一步到位捕捉到全局的联系,因为它直接把序列两两比较(代价是计算量变为$\mathcal{O}(n^2)$,当然由于是纯矩阵运算,这个计算量相当也不是很严重);相比之下,RNN需要一步步递推才能捕捉到,而CNN则需要通过层叠来扩大感受野,这是Attention层的明显优势。
Google论文剩下的工作,就是介绍它怎么用到机器翻译中,这是个应用和调参的问题,我们这里不特别关心它。当然,Google的结果表明将纯注意力机制用在机器翻译中,能取得目前最好的效果,这结果的确是辉煌的。
然而,我还是想谈谈这篇论文本身和Attention层自身的一些不足的地方。
1、论文标题为《Attention is All You Need》,因此论文中刻意避免出现了RNN、CNN的字眼,但我觉得这种做法过于刻意了。事实上,论文还专门命名了一种Position-wise Feed-Forward Networks,事实上它就是窗口大小为1的一维卷积,因此有种为了不提卷积还专门换了个名称的感觉,有点不厚道。(也有可能是我过于臆测了)
2、Attention虽然跟CNN没有直接联系,但事实上充分借鉴了CNN的思想,比如Multi-Head Attention就是Attention做多次然后拼接,这跟CNN中的多个卷积核的思想是一致的;还有论文用到了残差结构,这也源于CNN网络。
3、无法对位置信息进行很好地建模,这是硬伤。尽管可以引入Position Embedding,但我认为这只是一个缓解方案,并没有根本解决问题。举个例子,用这种纯Attention机制训练一个文本分类模型或者是机器翻译模型,效果应该都还不错,但是用来训练一个序列标注模型(分词、实体识别等),效果就不怎么好了。那为什么在机器翻译任务上好?我觉得原因是机器翻译这个任务并不特别强调语序,因此Position Embedding所带来的位置信息已经足够了,此外翻译任务的评测指标BLEU也并不特别强调语序。
4、并非所有问题都需要长程的、全局的依赖的,也有很多问题只依赖于局部结构,这时候用纯Attention也不大好。事实上,Google似乎也意识到了这个问题,因此论文中也提到了一个restricted版的Self-Attention(不过论文正文应该没有用到它),它假设当前词只与前后$r$个词发生联系,因此注意力也只发生在这$2r+1$个词之间,这样计算量就是$\mathcal{O}(nr)$,这样也能捕捉到序列的局部结构了。但是很明显,这就是卷积核中的卷积窗口的概念!
通过以上讨论,我们可以体会到,把Attention作为一个单独的层来看,跟CNN、RNN等结构混合使用,应该能更充分融合它们各自的优势,而不必像Google论文号称Attention is All You Need,那样实在有点“矫枉过正”了(“口气”太大),事实上也做不到。就论文的工作而言,也许降低一下身段,称为Attention is All Seq2Seq Need(事实上也这标题的“口气”也很大),会获得更多的肯定。
代码实现 #
最后,为了使得本文有点实用价值,笔者试着给出了论文的Multi-Head Attention的实现代码。有需要的读者可以直接使用,或者参考着修改。
注意的是,Multi-Head的意思虽然很简单——重复做几次然后拼接,但事实上不能按照这个思路来写程序,这样会非常慢。因为tensorflow是不会自动并行的,比如
a = tf.zeros((10, 10))
b = a + 1
c = a + 2
其中b,c的计算是串联的,尽管b、c没有相互依赖。因此我们必须把Multi-Head的操作合并到一个张量来运算,因为单个张量的乘法内部则会自动并行。
此外,我们要对序列做Mask以忽略填充部分的影响。一般的Mask是将填充部分置零,但Attention中的Mask是要在softmax之前,把填充部分减去一个大整数(这样softmax之后就非常接近0了)。这些内容都在代码中有对应的实现。
tensorflow版 #
下面是tf的实现:
https://github.com/bojone/attention/blob/master/attention_tf.py
Keras版 #
Keras仍然是我最喜爱的深度学习框架之一,因此必须也得给Keras写一个出来:
https://github.com/bojone/attention/blob/master/attention_keras.py
代码测试 #
在Keras上对IMDB进行简单的测试(不做Mask):
from __future__ import print_function
from keras.preprocessing import sequence
from keras.datasets import imdb
from attention_keras import *
max_features = 20000
maxlen = 80
batch_size = 32
print('Loading data...')
(x_train, y_train), (x_test, y_test) = imdb.load_data(num_words=max_features)
print(len(x_train), 'train sequences')
print(len(x_test), 'test sequences')
print('Pad sequences (samples x time)')
x_train = sequence.pad_sequences(x_train, maxlen=maxlen)
x_test = sequence.pad_sequences(x_test, maxlen=maxlen)
print('x_train shape:', x_train.shape)
print('x_test shape:', x_test.shape)
from keras.models import Model
from keras.layers import *
S_inputs = Input(shape=(None,), dtype='int32')
embeddings = Embedding(max_features, 128)(S_inputs)
# embeddings = SinCosPositionEmbedding(128)(embeddings) # 增加Position_Embedding能轻微提高准确率
O_seq = Attention(8,16)([embeddings,embeddings,embeddings])
O_seq = GlobalAveragePooling1D()(O_seq)
O_seq = Dropout(0.5)(O_seq)
outputs = Dense(1, activation='sigmoid')(O_seq)
model = Model(inputs=S_inputs, outputs=outputs)
# try using different optimizers and different optimizer configs
model.compile(loss='binary_crossentropy',
optimizer='adam',
metrics=['accuracy'])
print('Train...')
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=5,
validation_data=(x_test, y_test))
无Position Embedding的结果:
Train on 25000 samples, validate on 25000 samples
25000/25000 [==============================] - 9s - loss: 0.4090 - acc: 0.8126 - val_loss: 0.3541 - val_acc: 0.8430
Epoch 2/5
25000/25000 [==============================] - 9s - loss: 0.2528 - acc: 0.8976 - val_loss: 0.3962 - val_acc: 0.8284
Epoch 3/5
25000/25000 [==============================] - 9s - loss: 0.1731 - acc: 0.9335 - val_loss: 0.5172 - val_acc: 0.8137
Epoch 4/5
25000/25000 [==============================] - 9s - loss: 0.1172 - acc: 0.9568 - val_loss: 0.6185 - val_acc: 0.8009
Epoch 5/5
25000/25000 [==============================] - 9s - loss: 0.0750 - acc: 0.9730 - val_loss: 0.9310 - val_acc: 0.7925
有Position Embedding的结构:
Train on 25000 samples, validate on 25000 samples
Epoch 1/5
25000/25000 [==============================] - 9s - loss: 0.5179 - acc: 0.7183 - val_loss: 0.3540 - val_acc: 0.8413
Epoch 2/5
25000/25000 [==============================] - 9s - loss: 0.2880 - acc: 0.8786 - val_loss: 0.3464 - val_acc: 0.8447
Epoch 3/5
25000/25000 [==============================] - 9s - loss: 0.1584 - acc: 0.9404 - val_loss: 0.4398 - val_acc: 0.8313
Epoch 4/5
25000/25000 [==============================] - 9s - loss: 0.0588 - acc: 0.9803 - val_loss: 0.5836 - val_acc: 0.8243
Epoch 5/5
25000/25000 [==============================] - 9s - loss: 0.0182 - acc: 0.9947 - val_loss: 0.8095 - val_acc: 0.8178
貌似最高准确率比单层的LSTM准确率还高一点,另外还可以看到Position Embedding能提高准确率、减弱过拟合。
计算量分析 #
可以看到,事实上Attention的计算量并不低。比如Self Attention中,首先要对$\boldsymbol{X}$做三次线性映射,这计算量已经相当于卷积核大小为3的一维卷积了,不过这部分计算量还只是$\mathcal{O}(n)$的;然后还包含了两次序列自身的矩阵乘法,这两次矩阵乘法的计算量都是$\mathcal{O}(n^2)$的,要是序列足够长,这个计算量其实是很难接受的。
这也表明,restricted版的Attention是接下来的研究重点,并且将Attention与CNN、RNN混合使用,才是比较适中的道路。
结语 #
感谢Google提供的精彩的使用案例,让我等在大开眼界之余,还对Attention的认识更深一层。Google的这个成果在某种程度上体现了“大道至简”的理念,的确是NLP中不可多得的精品。本文围绕着Google的大作,班门弄斧一番,但愿能够帮助有需要的读者更好的理解Attention。最后恳请大家建议和批评。
转载到请包括本文地址:https://spaces.ac.cn/archives/4765
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Jan. 06, 2018). 《《Attention is All You Need》浅读(简介+代码) 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/4765
@online{kexuefm-4765,
title={《Attention is All You Need》浅读(简介+代码)},
author={苏剑林},
year={2018},
month={Jan},
url={\url{https://spaces.ac.cn/archives/4765}},
}











May 29th, 2018
O_seq = Attention(8,16)([embeddings,embeddings,embeddings]) 这行代码里的8和16表达什么意思
Multi-Head Attention中的$h$和$\tilde{d}_v$(请通读本文并对照源码)
July 2nd, 2018
感谢大佬的分享让我可以很快上手论文中的模型,不过在看代码的过程中我有几个问题希望大佬能帮我解答一下,谢谢。
1)论文中Attention部分QK相乘之后的mask是做什么用的呀,是为了避免在解码过程中使用到未来信息么?但是在解码又有专门的mask部分,希望您指点一下。还有我看代码中您似乎是先将softmax(QK)与V相乘之后再进行mask的,效果上有什么区别吗?
2)论文在每一个sublay之后接了一个Add&Norm层,但是输入的x和sublay的输出维度可能不一致,这一部分要怎么实现?
多谢指点
mask那个我似乎看懂了,应该是在需要mask的时候多传入两个参数就好了,但是Add&Norm部分还是不太明白
那就控制卷积的输出维度,让它们维度一致呗,不一致那不是自己找自己麻烦吗?
如果实在维度不一致,可以多加一步size=1的卷积,对输入调整一下维度后再加上输出,这是残差的基本用法了。
July 11th, 2018
请教!如果我想把模型预测的结果,也就是y_pred输出,该怎么写代码呢
August 23rd, 2018
苏神,你好。我对于position embeding 的代码有点问题,我觉得 位置向量的计算公式中间的 p 好像漏掉了。现在的代码,好像默认 p = 1,
\begin{aligned}&PE_{2i}(p)=\sin\Big(p/10000^{2i/{d_{pos}}}\Big)\\
&PE_{2i+1}(p)=\cos\Big(p/10000^{2i/{d_{pos}}}\Big)
\end{aligned}
tf版本中有tf.range这一句,配合matmul就已经实现了乘以$p$;Keras版本中有K.cumsum(K.ones_like(x[:,:,0]), 1)-1这一句,配合dot就可以实现乘以$p$
September 2nd, 2018
postion embedding 怎么理解啊,我理解这个模型是能捕捉序列顺序的。您说“如果打乱计算attention的K, V的顺序,attention的结果仍然d是一样的,所以这个模型并不能捕捉序列顺序”。但是Query的顺序是有的啊,输出的向量序列和Query向量序列是能对上的。
attention的大概意思是“查找文档中与query最相近的词”,如果没有postion embedding,如果一个词在文章中多次出现的话,它没法区分第几个词,也没法区分这个词的隔壁是什么词。
query是有顺序的,也就是输出token是对应着输出token的顺序 但是attention里面每个token和所有token交互的时候,是不考虑顺序的,就是x0在和x1和x2做attention的时候是不知道他们在哪里的。因为是加权求和的操作,这个操作是不考虑顺序的,原因就是加法满足交换律
September 4th, 2018
明白了,就是说同样的词在不同位置出现,attention的结果应该是有区别的,所以引入了position embedding。
那比如说在图像领域中,例如文本行识别,先用cnn得到一个特征序列x(x1,x2,...,xn),因为这里每个query向量xi与其它向量几乎不同,是不是没必要用Position embedding了?您怎么看?
文本识别中不涉及到global pooling的话,基本上用不着position embedding,都只是局部识别而已,而且用的是CNN,CNN是局部有序的,纯Attention是完全无序的,这就是差别。
我没描述完整,这个特征序列x(x1,x2,...,xn)是作为输入,后面接这篇论文的结构。是否有必要对xi这些query向量加position embedding? 我的理解是不用加的。 但是有论文用这种结构做文本行识别,当然他也没讨论这个position embedding,直接套用了
September 11th, 2018
我想用mask,在Attention的源码中要传入Q_len,V_len两个参数,请问它们是指Q_seq和V_seq的长度吗?是几维的张量?
shape=(None,1)的整型张量
September 16th, 2018
请教一下,attention层的要训练的模型参数是什么?是K和V吗?
还有,self-attention的模型参数是不是不一样?只需要训练MultiHead的映射矩阵W吗?
https://kexue.fm/archives/4765#Multi-Head%20Attention
都是$W$
请问对于不是self-attention的情况,也就是K≠X且V≠X,这种attention机制的K和V是如何得到呢?是当作模型参数由训练过程得到吗?
这个疑问表明你根本就不理解attention的作用,attention的主要成份是$Q,K,V$,可以理解为带着问题$Q$到资料$K,V$里边找答案。$K,V$相当于被查询的资料,你不把资料传给模型,你还想模型自己造资料么?
所以答案很明显,如果不是self-attention,那就你自己把$K,V$传给模型...
September 20th, 2018
老师,attention层中的几个映射矩阵都是需要学习的吗,我想在编码器的self-attention层后面加上一个自编码器做特征提取,损失函数是原来的均方误差么,是用bp算法来训练吗?
老师,我大概明白了,如果是self_attention层,则训练的几个映射矩阵参数都是W,是一样的,在其后面加上自编码器的话训练不了W,因为自编码器相当于无监督学习,那如果在自编码器后面加上一个softmax层进行有监督训练,整个模型的损失函数可以是什么样的呢?
self_attention输入一个向量序列,输出也是一个向量序列,我不知道你的自编码器是什么意思。
October 7th, 2018
[...]《Attention is All You Need》浅读(简介+代码)[...]