科学空间|Scientific Spaces

笔者发现，有很多概率问题，尤其是独立重复实验问题，如果用生成函数的方法来做，会显得特别方便。本文要讲的“随机游走”问题便是其中一例，它又被形象地叫做“醉汉问题”，其本质上是一个二项分布，但是由于取了极限，出现了很多新的性质和应用。我们先考虑如下问题：

考虑实数轴上的一个粒子，在$t=0$时刻它位于原点，每过一秒，它要不向前移动一格（+1），要不就向后移动一格（-1），问$n$秒后它所处位置的概率分布。

点击阅读全文...

我们在上一篇文章中已经看到，随机游走的概率分布是正态的，而在概率论中可以了解到正态分布（几乎）是最重要的一种分布了。随机游走模型和正态分布的应用都很广，我们或许可以思考一个问题，究竟是随机游走造就了正态分布，还是正态分布造就了随机游走？换句话说，哪个更本质些？个人就自己目前所阅读到的内容来看，随机游走更本质些，随机游走正好对应着普遍存在的随机不确定性（比如每次测量的误差），它的分布正好就是正态分布，所以正态分布才应用得如此广泛——因为随机不确定性无处不在。

下面我们来考虑随机游走的另外一种描述方式，原则上来说，它更广泛，更深刻，其大名曰“路径积分”。

点击阅读全文...

本文我们继续之前的变分自编码器系列，分析一下如何防止NLP中的VAE模型出现“KL散度消失（KL Vanishing）”现象。本文受到参考文献是ACL 2020的论文《A Batch Normalized Inference Network Keeps the KL Vanishing Away》的启发，并自行做了进一步的完善。

值得一提的是，本文最后得到的方案还是颇为简洁的——只需往编码输出加入BN（Batch Normalization），然后加个简单的scale——但确实很有效，因此值得正在研究相关问题的读者一试。同时，相关结论也适用于一般的VAE模型（包括CV的），如果按照笔者的看法，它甚至可以作为VAE模型的“标配”。

最后，要提醒读者这算是一篇VAE的进阶论文，所以请读者对VAE有一定了解后再来阅读本文。

VAE简单回顾

这里我们简单回顾一下VAE模型，并且讨论一下VAE在NLP中所遇到的困难。关于VAE的更详细介绍，请读者参考笔者的旧作《变分自编码器（一）：原来是这么一回事》、《变分自编码器（二）：从贝叶斯观点出发》等。

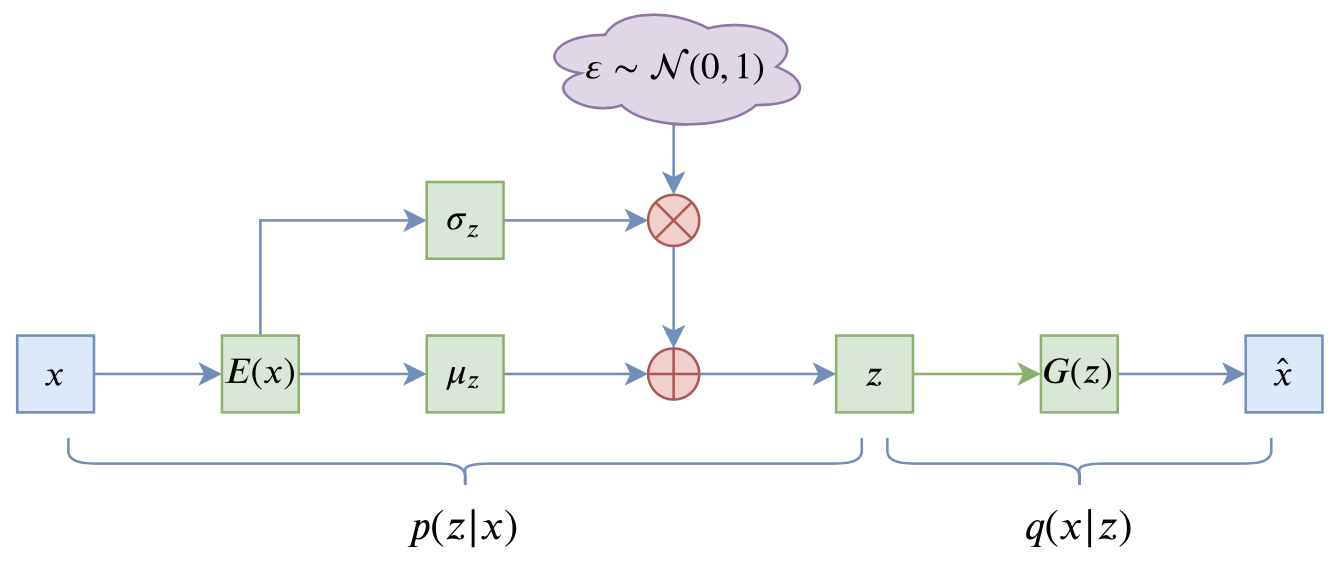
VAE的训练流程

VAE的训练流程大概可以图示为

VAE训练流程图示

点击阅读全文...

特殊的通项公式

对数学或编程感兴趣的读者，相信都已经很熟悉斐波那契数列了

0, 1, 1, 2, 3, 5, 8, 13, ...

它是由
$$a_{n+2}=a_{n+1}+a_n,\quad a_0=0,a_1=1$$
递推所得。读者或许已经见过它的通项公式
$$a_{n}=\frac{\sqrt{5}}{5} \cdot \left[\left(\frac{1 + \sqrt{5}}{2}\right)^{n} - \left(\frac{1 - \sqrt{5}}{2}\right)^{n}\right]$$
这里假设我们没有如此高的智商可以求出这个复杂的表达式出来，但是我们通过研究数列发现，这个数列越来越大时，相邻两项趋于一个常数，这个常数也就是（假设我们只发现了后面的数值，并没有前面的根式）
$$\beta=\frac{1 + \sqrt{5}}{2}=1.61803398\dots$$

点击阅读全文...

在2018年的文章里《f-GAN简介：GAN模型的生产车间》笔者介绍了f-GAN，并评价其为GAN模型的“生产车间”，顾名思义，这是指它能按照固定的流程构造出很多不同形式的GAN模型来。前几天在arxiv上看到了新出的一篇论文《Designing GANs: A Likelihood Ratio Approach》（后面简称Designing GANs或原论文），发现它在做跟f-GAN同样的事情，但走的是一条截然不同的路（不过最后其实是殊途同归），整篇论文颇有意思，遂在此分享一番。

f-GAN回顾

从《f-GAN简介：GAN模型的生产车间》中我们可以知道，f-GAN的首要步骤是找到满足如下条件的函数$f$：

1、$f$是非负实数到实数的映射（$\mathbb{R}^* \to \mathbb{R}$）；

2、$f(1)=0$；

3、$f$是凸函数。

点击阅读全文...

前言：一年前国赛的时候，很初级地做了一下B题，做完之后还写了个《碎纸复原：一个人的数学建模》。当时就是对题目很有兴趣，然后通过一天的学习，基本完成了附件一二的代码，对附件三也只是有个概念。而今年我们上的数学建模课，老师把这道题作为大作业让我们做，于是我便再拾起了一年前的那份激情，继续那未完成的一个人的数学建模...

与去年不同的是，这次将所有代码用Python实现了，更简洁，更清晰，甚至可能更高效~~以下是论文全文。

研究背景

2011年10月29日，美国国防部高级研究计划局（DARPA）宣布了一场碎纸复原挑战赛（Shredder Challenge），旨在寻找到高效有效的算法，对碎纸机处理后的碎纸屑进行复原。[1]该竞赛吸引了全美9000支参赛队伍参与角逐，经过一个多月的时间，有一支队伍成功完成了官方的题目。

近年来，碎纸复原技术日益受到重视，它显示了在碎片中“还原真相”的可能性，表明我们可以从一些破碎的片段中“解密”出原始信息来。另一方面，该技术也和照片处理领域中的“全景图拼接技术”有一定联系，该技术是指通过若干张不同侧面的照片，合成一张完整的全景图。因此，分析研究碎纸复原技术，有着重要的意义。

点击阅读全文...

fashion_mnist_demo

mnist的手写数字识别数据集一直是各种机器学习算法的试金石之一，最近有个新的数据集要向它叫板，称为fashion-mnist，内容是衣服鞋帽等分类。为了便于用户往fashion-mnist迁移，作者把数据集做成了几乎跟mnist手写数字识别数据集一模一样——同样数量、尺寸的图片，同样是10分类，甚至连数据打包和命名都跟mnist一样。看来fashion mnist为了取代mnist，也是拼了，下足了功夫，一切都做得一模一样，最大限度降低了使用成本～这叫板的心很坚定呀。

叫板的原因很简单——很多人吐槽，如果一个算法在mnist没用，那就一定没用了，但如果一个算法在mnist上有效，那它也不见得在真实问题中有效～也就是说，这个数据集太简单，没啥代表性。

fashion-mnist的github：https://github.com/zalandoresearch/fashion-mnist/

点击阅读全文...

神经网络

在所有机器学习模型之中，也许最有趣、最深刻的便是神经网络模型了。笔者也想献丑一番，说一次神经网络。当然，本文并不打算从头开始介绍神经网络，只是谈谈我对神经网络的个人理解。如果希望进一步了解神经网络与深度学习的朋友，请移步阅读下面的教程：
http://deeplearning.stanford.edu/wiki/index.php/UFLDL教程

http://blog.csdn.net/zouxy09/article/details/8775360

机器分类

这里以分类工作为例，数据挖掘或机器学习中，有很多分类的问题，比如讲一句话的情况进行分类，粗略点可以分类为“积极”或“消极”，精细点分为开心、生气、忧伤等；另外一个典型的分类问题是手写数字识别，也就是将图片分为10类（0,1,2,3,4,5,6,7,8,9）。因此，也产生了很多分类的模型。

点击阅读全文...