科学空间|Scientific Spaces

BN，也就是Batch Normalization，是当前深度学习模型（尤其是视觉相关模型）的一个相当重要的技巧，它能加速训练，甚至有一定的抗过拟合作用，还允许我们用更大的学习率，总的来说颇多好处（前提是你跑得起较大的batch size）。

那BN究竟是怎么起作用呢？早期的解释主要是基于概率分布的，大概意思是将每一层的输入分布都归一化到$\mathcal{N}(0,1)$上，减少了所谓的Internal Covariate Shift，从而稳定乃至加速了训练。这种解释看上去没什么毛病，但细思之下其实有问题的：不管哪一层的输入都不可能严格满足正态分布，从而单纯地将均值方差标准化无法实现标准分布$\mathcal{N}(0,1)$；其次，就算能做到$\mathcal{N}(0,1)$，这种诠释也无法进一步解释其他归一化手段（如Instance Normalization、Layer Normalization）起作用的原因。

在去年的论文《How Does Batch Normalization Help Optimization?》里边，作者明确地提出了上述质疑，否定了原来的一些观点，并提出了自己关于BN的新理解：他们认为BN主要作用是使得整个损失函数的landscape更为平滑，从而使得我们可以更平稳地进行训练。

本博文主要也是分享这篇论文的结论，但论述方法是笔者“闭门造车”地构思的。窃认为原论文的论述过于晦涩了，尤其是数学部分太不好理解，所以本文试图尽可能直观地表达同样观点。

（注：阅读本文之前，请确保你已经清楚知道BN是什么，本文不再重复介绍BN的概念和流程。）

点击阅读全文...

当前，说到深度学习中的对抗，一般会有两个含义：一个是生成对抗网络（Generative Adversarial Networks，GAN），代表着一大类先进的生成模型；另一个则是跟对抗攻击、对抗样本相关的领域，它跟GAN相关，但又很不一样，它主要关心的是模型在小扰动下的稳健性。本博客里以前所涉及的对抗话题，都是前一种含义，而今天，我们来聊聊后一种含义中的“对抗训练”。

本文包括如下内容：

1、对抗样本、对抗训练等基本概念的介绍；

2、介绍基于快速梯度上升的对抗训练及其在NLP中的应用；

3、给出了对抗训练的Keras实现（一行代码调用）；

4、讨论了对抗训练与梯度惩罚的等价性；

5、基于梯度惩罚，给出了一种对抗训练的直观的几何理解。

点击阅读全文...

生成模型一直是笔者比较关注的主题，不管是NLP和CV的生成模型都是如此。这篇文章里，我们介绍一个新颖的生成模型，来自论文《Batch norm with entropic regularization turns deterministic autoencoders into generative models》，论文中称之为EAE（Entropic AutoEncoder）。它要做的事情给变分自编码器（VAE）基本一致，最终效果其实也差不多（略优），说它新颖并不是它生成效果有多好，而是思路上的新奇，颇有别致感。此外，借着这个机会，我们还将学习一种统计量的估计方法——$k$邻近方法，这是一种很有用的非参数估计方法。

自编码器vs生成模型

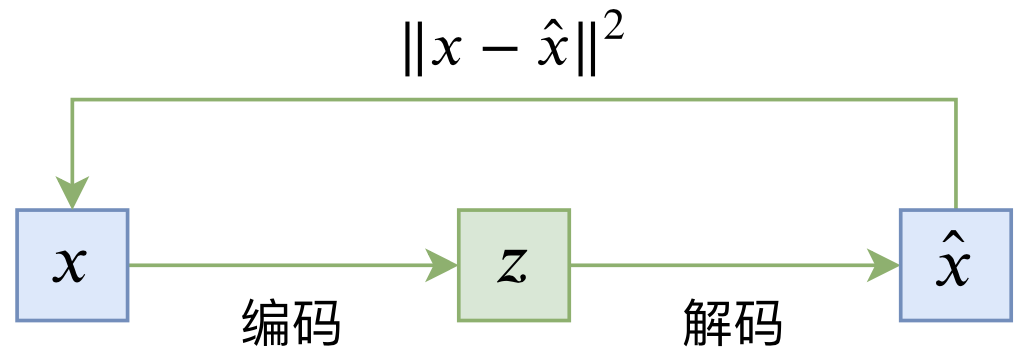
普通的自编码器是一个“编码-解码”的重构过程，如下图所示：

典型自编码器示意图

其loss一般为
\begin{equation}L_{AE} = \mathbb{E}_{x\sim \tilde{p}(x)}\left[\left\Vert x - \hat{x}\right\Vert^2\right] = \mathbb{E}_{x\sim \tilde{p}(x)}\left[\left\Vert x - D(E(x))\right\Vert^2\right]\end{equation}

点击阅读全文...

本文介绍来自MIT的一篇ICLR 2020满分论文《Why gradient clipping accelerates training: A theoretical justification for adaptivity》，顾名思义，这篇论文就是分析为什么梯度裁剪能加速深度学习的训练过程。原文很长，公式很多，还有不少研究复杂性的概念，说实话对笔者来说里边的大部分内容也是懵的，不过大概能捕捉到它的核心思想：引入了比常用的L约束更宽松的约束条件，从新的条件出发论证了梯度裁剪的必要性。本文就是来简明分析一下这个过程，供读者参考。

梯度裁剪

假设需要最小化的函数为$f(\theta)$，$\theta$就是优化参数，那么梯度下降的更新公式就是
\begin{equation}\theta \leftarrow \theta-\eta \nabla_{\theta} f(\theta)\end{equation}
其中$\eta$就是学习率。而所谓梯度裁剪（gradient clipping），就是根据梯度的模长来对更新量做一个缩放，比如
\begin{equation}\theta \leftarrow \theta- \eta \nabla_{\theta} f(\theta)\times \min\left\{1, \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert}\right\}\label{eq:clip-1}\end{equation}
或者
\begin{equation}\theta \leftarrow \theta- \eta \nabla_{\theta} f(\theta)\times \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert+\gamma}\label{eq:clip-2}\end{equation}
其中$\gamma > 0$是一个常数。这两种方式都被视为梯度裁剪，总的来说就是控制更新量的模长不超过一个常数，第二种形式也跟RMSProp等自适应学习率优化器相关。此外，更精确地，我们有下面的不等式
\begin{equation}\frac{1}{2}\min\left\{1, \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert}\right\}\leq \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert+\gamma}\leq \min\left\{1, \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert}\right\}\end{equation}
也就是说两者是可以相互控制的，所以其实两者基本是等价的。

点击阅读全文...

不少读者都应该知道，损失函数与评测指标的不一致性是机器学习的典型现象之一，比如分类问题中损失函数用交叉熵，评测指标则是准确率或者F1，又比如文本生成中损失函数是teacher-forcing形式的交叉熵，评测指标则是BLEU、ROUGE等。理想情况下，当然是评测什么指标，我们就去优化这个指标，然而评测指标通常都是不可导的，而我们多数都是使用基于梯度的优化器，这就要求最小化的目标必须是可导的，这是不一致性的来源。

前些天在arxiv刷到了一篇名为《MLE-guided parameter search for task loss minimization in neural sequence modeling》的论文，顾名思义，它是研究如何直接优化文本生成的评测指标的。经过阅读，笔者发现这篇论文很有价值，事实上它提供了一种优化评测指标的新思路，适用范围并不局限于文本生成中。不仅如此，它甚至还包含了一种理解可导优化与不可导优化的统一视角。

采样视角

首先，我们可以通过采样的视角来重新看待优化问题：设模型当前参数为$\theta$，优化目标为$l(\theta)$，我们希望决定下一步的更新量$\Delta\theta$，为此，我们先构建分布
\begin{equation}p(\Delta\theta|\theta)=\frac{e^{-[l(\theta + \Delta\theta) - l(\theta)]/\alpha}}{Z(\theta)},\quad Z(\theta) = \int e^{-[l(\theta + \Delta\theta) - l(\theta)]/\alpha} d(\Delta\theta)\end{equation}

点击阅读全文...

类别不平衡问题，也叫“长尾问题”，是机器学习面临的常见问题之一，尤其是来源于真实场景下的数据集，几乎都是类别不平衡的。大概在两年前，笔者也思考过这个问题，当时正好对“互信息”相关的内容颇有心得，所以构思了一种基于互信息思想的解决办法，但又想了一下，那思路似乎过于平凡，所以就没有深究。然而，前几天在arxiv上刷到Google的一篇文章《Long-tail learning via logit adjustment》，意外地发现里边包含了跟笔者当初的构思几乎一样的方法，这才意识到当初放弃的思路原来还能达到SOTA的水平～于是结合这篇论文，将笔者当初的构思过程整理于此，希望不会被读者嫌弃“马后炮”。

问题描述

这里主要关心的是单标签的多分类问题，假设有$1,2,\cdots,K$共$K$个候选类别，训练数据为$(x,y)\sim\mathcal{D}$，建模的分布为$p_{\theta}(y|x)$，那么我们的优化目标是最大似然，或者说最小化交叉熵，即
\begin{equation}\mathop{\text{argmin}}_{\theta}\,\mathbb{E}_{(x,y)\sim\mathcal{D}}[-\log p_{\theta}(y|x)]\end{equation}

点击阅读全文...

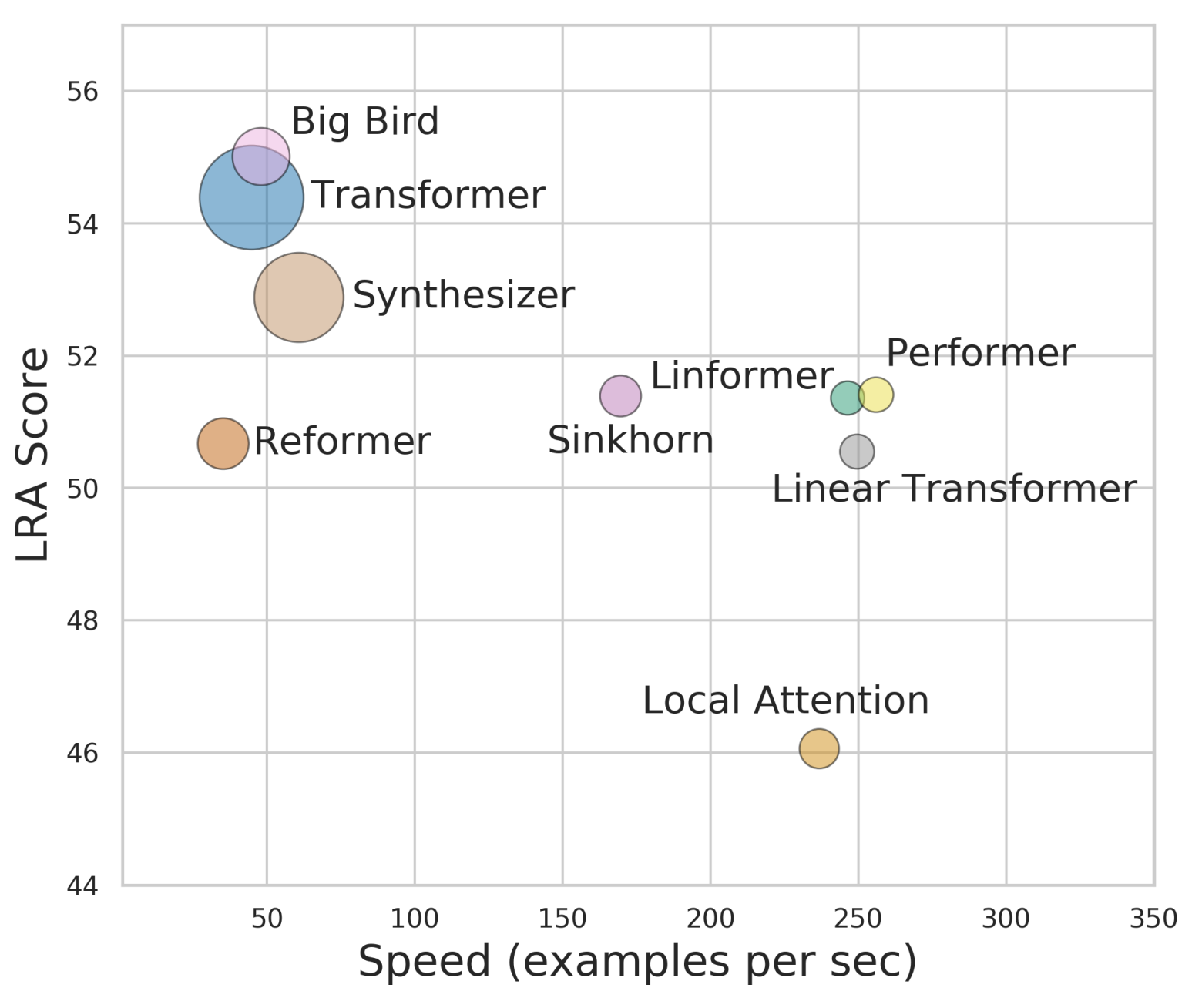
Attention机制的$\mathcal{O}(n^2)$复杂度是一个老大难问题了，改变这一复杂度的思路主要有两种：一是走稀疏化的思路，比如我们以往介绍过的Sparse Attention以及Google前几个月搞出来的Big Bird，等等；二是走线性化的思路，这部分工作我们之前总结在《线性Attention的探索：Attention必须有个Softmax吗？》中，读者可以翻看一下。本文则介绍一项新的改进工作Performer，出自Google的文章《Rethinking Attention with Performers》，它的目标相当霸气：通过随机投影，在不损失精度的情况下，将Attention的复杂度线性化。

各个Transformer模型的“效果-速度-显存”图，纵轴是效果，横轴是速度，圆圈的大小代表所需要的显存。理论上来说，越靠近右上方的模型越好，圆圈越小的模型越好

说直接点，就是理想情况下我们可以不用重新训练模型，输出结果也不会有明显变化，但是复杂度降到了$\mathcal{O}(n)$！看起来真的是“天上掉馅饼”般的改进了，真的有这么美好吗？

点击阅读全文...

“法研杯”算是近年来比较知名的NLP赛事之一，今年是第三届，包含四个赛道，其中有一个“司法摘要”赛道引起了我们的兴趣。经过了解，这是面向法律领域裁判文书的长文本摘要生成，这应该是国内第一个公开的长文本生成任务和数据集。过去一年多以来，我们在文本生成方面都有持续的投入和探索，所以决定选择该赛道作为检验我们研究成果的“试金石”。很幸运，我们最终以微弱的优势获得了该赛道的第一名。在此，我们对我们的比赛模型做一个总结和分享。

比赛榜单截图

在该比赛中，我们跳出了纯粹炼丹的过程，通过新型的Copy机制、Sparse Softmax等颇具通用性的新方法提升了模型的性能。整体而言，我们的模型比较简洁有效，而且可以做到端到端运行。窃以为我们的结果对工程和研究都有一定的参考价值。

点击阅读全文...