通过互信息思想来缓解类别不平衡问题
By 苏剑林 | 2020-07-19 | 238821位读者 |类别不平衡问题,也叫“长尾问题”,是机器学习面临的常见问题之一,尤其是来源于真实场景下的数据集,几乎都是类别不平衡的。大概在两年前,笔者也思考过这个问题,当时正好对“互信息”相关的内容颇有心得,所以构思了一种基于互信息思想的解决办法,但又想了一下,那思路似乎过于平凡,所以就没有深究。然而,前几天在arxiv上刷到Google的一篇文章《Long-tail learning via logit adjustment》,意外地发现里边包含了跟笔者当初的构思几乎一样的方法,这才意识到当初放弃的思路原来还能达到SOTA的水平~于是结合这篇论文,将笔者当初的构思过程整理于此,希望不会被读者嫌弃“马后炮”。
问题描述 #
这里主要关心的是单标签的多分类问题,假设有$1,2,\cdots,K$共$K$个候选类别,训练数据为$(x,y)\sim\mathcal{D}$,建模的分布为$p_{\theta}(y|x)$,那么我们的优化目标是最大似然,或者说最小化交叉熵,即
\begin{equation}\mathop{\text{argmin}}_{\theta}\,\mathbb{E}_{(x,y)\sim\mathcal{D}}[-\log p_{\theta}(y|x)]\end{equation}
通常来说,我们建立的概率模型最后一步都是softmax,假设softmax之前的结果为$f(x;\theta)$(即logits),那么
\begin{equation}-\log p_{\theta}(y|x)=-\log \frac{e^{f_y(x;\theta)}}{\sum\limits_{i=1}^K e^{f_i(x;\theta)}}=\log\left[1 + \sum_{i\neq y}e^{f_i(x;\theta) - f_y(x;\theta)}\right]\label{eq:loss-1}\end{equation}
所谓类别不均衡,就是指某些类别的样本特别多,就好比“20%的人占据了80%的财富”一样,剩下的类别数很多,但是总样本数很少,如果从高到低排序的话,就好像带有一条很长的“尾巴”,所以叫做长尾现象。这种情况下,我们训练的时候采样一个batch,很少有机会采样到低频类别,因此很容易被模型忽略了低频类。但评测的时候,通常我们又更关心低频类别的识别效果,这便是矛盾之处。
常见思路 #
常见的思路大家应该也有所听说,大概就是三个方向:
1、从数据入手,通过过采样或降采样等手段,使得每个batch内的类别变得更为均衡一些;
2、从loss入手,经典的做法就是类别$y$的样本loss除以类别出现的频率$p(y)$;
3、从结果入手,对正常训练完的模型在预测阶段做些调整,更偏向于低频类别,比如正样本远少于负样本,我们可以把预测结果大于0.2(而不是0.5)都视为正样本。
Google的原论文中对这三个方向的思路也列举了不少参考文献,有兴趣调研的读者可以直接阅读原论文,另外,知乎上的文章《Long-Tailed Classification (2) 长尾分布下分类问题的最新研究》也对该问题进行了介绍,读者也可以参考阅读。
学习互信息 #
回想一下,我们是怎么断定某个分类问题是不均衡的呢?显然,一般的思路是从整个训练集里边统计出各个类别的频率$p(y)$,然后发现$p(y)$集中在某几个类别中。所以,解决类别不平衡问题的重点,就是如何把这个先验知识$p(y)$融入模型之中。
在之前构思词向量模型(如文章《更别致的词向量模型(二):对语言进行建模》)的时候,我们就强调过,相比拟合条件概率,如果模型能直接拟合互信息,那么将会学习到更本质的知识,因为互信息才是揭示核心关联的指标。但是拟合互信息没那么容易训练,容易训练的是条件概率,直接用交叉熵$-\log p_{\theta}(y|x)$进行训练就行了。所以,一个比较理想的想法就是:如何使得模型依然使用交叉熵为loss,但本质上是在拟合互信息?
在公式$\eqref{eq:loss-1}$中,我们是建模了
\begin{equation}p_{\theta}(y|x)=\frac{e^{f_y(x;\theta)}}{\sum\limits_{i=1}^K e^{f_i(x;\theta)}}\end{equation}
现在我们改为建模互信息,那么也就是希望
\begin{equation}\log \frac{p_{\theta}(y|x)}{p(y)}\sim f_y(x;\theta)\quad \Leftrightarrow\quad \log p_{\theta}(y|x)\sim f_y(x;\theta) + \log p(y)\end{equation}
按照右端的形式重新进行softmax归一化,那么就有$p_{\theta}(y|x)=\frac{e^{f_y(x;\theta)+\log p(y)}}{\sum\limits_{i=1}^K e^{f_i(x;\theta)+\log p(i)}}$,或者写成loss形式:
\begin{equation}-\log p_{\theta}(y|x)=-\log \frac{e^{f_y(x;\theta)+\log p(y)}}{\sum\limits_{i=1}^K e^{f_i(x;\theta)+\log p(i)}}=\log\left[1 + \sum_{i\neq y}\frac{p(i)}{p(y)}e^{f_i(x;\theta) - f_y(x;\theta)}\right]\label{eq:loss-2}\end{equation}
原论文称之为logit adjustment loss。如果更加一般化,那么还可以加个调节因子$\tau$:
\begin{equation}-\log p_{\theta}(y|x)=-\log \frac{e^{f_y(x;\theta)+\tau\log p(y)}}{\sum\limits_{i=1}^K e^{f_i(x;\theta)+\tau\log p(i)}}=\log\left[1 + \sum_{i\neq y}\left(\frac{p(i)}{p(y)}\right)^{\tau}e^{f_i(x;\theta) - f_y(x;\theta)}\right]\label{eq:loss-3}\end{equation}
一般情况下,$\tau=1$的效果就已经接近最优了。如果$f_y(x;\theta)$的最后一层有bias项的话,那么最简单的实现方式就是将bias项初始化为$\tau\log p(y)$。也可以写在损失函数中:
import numpy as np
import keras.backend as K
def categorical_crossentropy_with_prior(y_true, y_pred, tau=1.0):
"""带先验分布的交叉熵
注:y_pred不用加softmax
"""
prior = xxxxxx # 自己定义好prior,shape为[num_classes]
log_prior = K.constant(np.log(prior + 1e-8))
for _ in range(K.ndim(y_pred) - 1):
log_prior = K.expand_dims(log_prior, 0)
y_pred = y_pred + tau * log_prior
return K.categorical_crossentropy(y_true, y_pred, from_logits=True)
def sparse_categorical_crossentropy_with_prior(y_true, y_pred, tau=1.0):
"""带先验分布的稀疏交叉熵
注:y_pred不用加softmax
"""
prior = xxxxxx # 自己定义好prior,shape为[num_classes]
log_prior = K.constant(np.log(prior + 1e-8))
for _ in range(K.ndim(y_pred) - 1):
log_prior = K.expand_dims(log_prior, 0)
y_pred = y_pred + tau * log_prior
return K.sparse_categorical_crossentropy(y_true, y_pred, from_logits=True)结果分析 #
很明显logit adjustment loss也属于调整loss方案之一,不同的是它是在$\log$里边调整权重,而常规的思路则是在$\log$外调整。至于它的好处,就是互信息的好处:互信息揭示了真正重要的关联,所以给logits补上先验分布的bias,能让模型做到“能靠先验解决的就靠先验解决,先验解决不了的本质部分才由模型解决”。
在预测阶段,根据不同的评测指标,我们可以制定不同的预测方案。从《函数光滑化杂谈:不可导函数的可导逼近》可以知道,对于整体准确率而言,我们有近似
\begin{equation}\text{整体准确率} \approx \frac{1}{N}\sum_{i=1}^N p_{\theta}(y_i|x_i)\end{equation}
其中$\{(x_i,y_i)\}_{i=1}^N$是验证集。所以如果不考虑类别不均衡情况,追求更高的整体准确率,那么对于每个$x$我们直接输出$p_{\theta}(y|x)$最大的类别即可。但如果我们希望每个类的准确率都尽可能高,那么我们将上式改写成
\begin{equation}\text{整体准确率} \approx \frac{1}{N}\sum_{i=1}^N \frac{p_{\theta}(y_i|x_i)}{p(y_i)}\times p(y_i)=\sum_{y=1}^K p(y)\left(\frac{1}{N}\sum_{x_i\in\Omega_y} \frac{p_{\theta}(y|x_i)}{p(y)}\right)\end{equation}
其中$\Omega_y=\{x_i|y_i=y,i=1,2,\cdots,N\}$,也标签为$y$的$x$的集合,等号右边事实上就是先将同一个$y$的项合并起来。我们知道“整体准确率=每一类的准确率的加权平均”,而上式正好具有同样的形式,所以括号里边的$\frac{1}{N}\sum\limits_{x_i\in\Omega_y} \frac{p_{\theta}(y|x_i)}{p(y)}$就是“每一类的准确率”的一个近似了,因此,如果我们希望每一类的准确率都尽可能高,我们则要输出使得$\frac{p_{\theta}(y|x)}{p(y)}$最大的类别(不加权)。结合$p_{\theta}(y|x)$的形式,我们有结论
\begin{equation}y^{*}=\left\{\begin{aligned}&\mathop{\text{argmax}}\limits_y\, f_y(x;\theta)+\tau\log p(y),\quad(\text{追求整体准确率})\\
&\mathop{\text{argmax}}\limits_y\, f_y(x;\theta),\quad(\text{希望每一类的准确率都尽可能均匀})
\end{aligned}\right.\end{equation}
第一种其实就是输出条件概率最大者,而第二种就是输出互信息最大者,按具体需求选择。
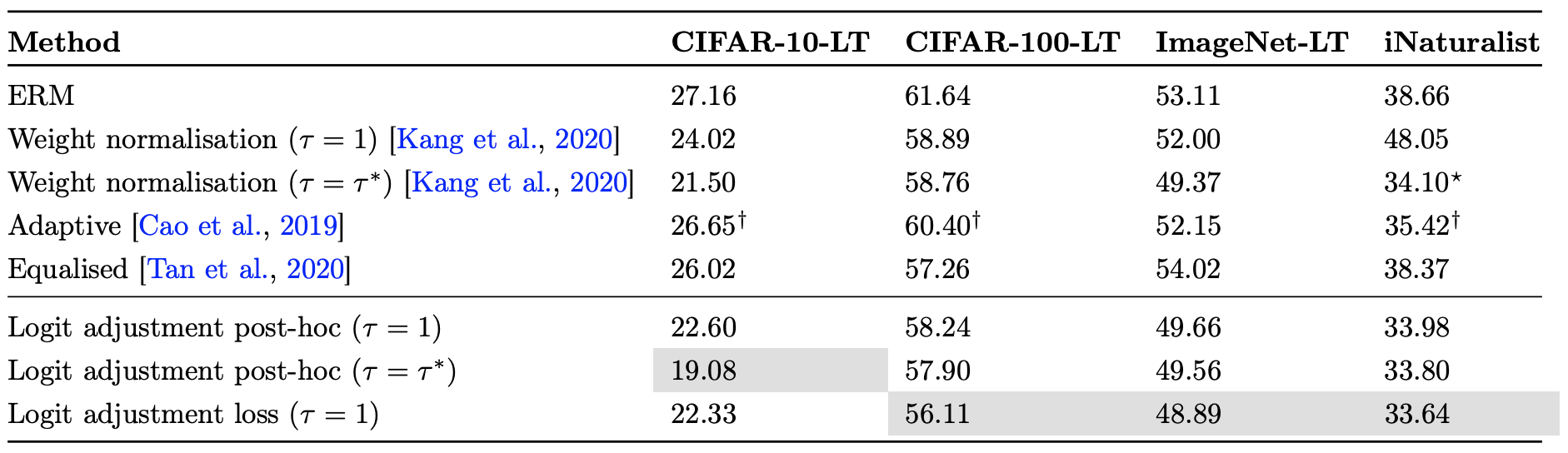
至于详细的实验结果,大家可以自行看论文,总之就是好到有点意外:
文章小结 #
本文简单介绍了一种基于互信息思想的类别不平衡处理办法,该方案以前笔者也曾经构思过,不过没有深究,而最近Google的一篇论文也给出了同样的方法,遂在此简单记录分析一下,最后Google给出的实验结果显示该方法能达到SOTA的水平。
转载到请包括本文地址:https://spaces.ac.cn/archives/7615
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Jul. 19, 2020). 《通过互信息思想来缓解类别不平衡问题 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/7615
@online{kexuefm-7615,
title={通过互信息思想来缓解类别不平衡问题},
author={苏剑林},
year={2020},
month={Jul},
url={\url{https://spaces.ac.cn/archives/7615}},
}










April 3rd, 2022
调用带先验的交叉熵损失函数时出现如下错误:
NotImplementedError: Cannot convert a symbolic Tensor (categorical_crossentropy_with_prior/add:0) to a numpy array. This error may indicate that you're trying to pass a Tensor to a NumPy call, which is not supported
请问这是怎么回事呢,用原始的交叉熵损失函数是可以正常训练的~
np.log改为K.log试试看。
我把1e-8去掉了模型就能训练了,去掉1e-8应该没啥影响吧?
这层就是我,之前的号登不上了~
挺神奇。没有NAN就不会有影响。
谢谢!
January 9th, 2023
您好,我有两个疑问:
1、建模互信息由nlp引出,但nlp的词在$P(w|context)$中是既可以做w,也可以做context的,本身就具有对称性。但长尾分类问题模型建模的是$P(y|x)$,图片表征x并不具有这种既能当x又能当y的“对称性”,那么怎么理解长尾分类这里的互信息呢?
2、$log\frac{p_{\theta} (y|x)}{p(y)}$建模了什么与什么的互信息?就好比$\frac{P(\omega _{1},\omega _{2})}{P(\omega _{1})P(\omega _{2})}$建模了上下文词和目标词间的互信息
望解答,谢谢
词向量模型的所谓“对称性”,我认为是初学者理解互信息的最大绊脚石!!没有之一!!!
点互信息的定义就是$\log\frac{p(X,Y)}{p(X)p(Y)}$或$\log\frac{p(Y|X)}{p(Y)}$,描述的就是随机变量$X,Y$的互信息。$p(X,Y)$是一个联合分布,$X$是第一个随机变量,$Y$是第二个随机变量,两个随机变量的取值可以是同一空间(比如都是词),也可以是不同空间(比如一个是图,一个是文)
请区分“随机变量”和“随机变量的取值”。
更具体些,假设$X$表示上下文的词,$Y$表示中心词,那么$p(X=x,Y=y)$就表示“上下文出现$x$、中心词为$y$”的概率(不误解的时候我们才记为$p(x,y)$),$p(X=y,Y=x)$就表示“上下文出现$y$、中心词为$x$”的概率,这难道不是两个看上去就不一定相等的东西吗?(除非我们故意设计它们相等,但这是故意的,跟互信息没关系)这是$X,Y$分别取不同值的两个case,只不过由于取值空间相同,两者交换也是有定义,只是有定义。假设$X$表示文,$Y$表示图,那么$p(X=x,Y=y)$就表示“图$x$和文$y$同时”的概率,这种交换就没定义了。
首先非常感谢您非常及时的回复和解答!
我有这个疑问主要是刚才看了您的这篇 https://spaces.ac.cn/archives/4669 ,第一部分提到之前的词向量模型$P(w|context)$是条件概率,是不对称的。这确实也是“直觉上”互信息比条件概率在nlp更适合的原因那么在分类问题上,直觉上互信息比条件概率好在哪?或者说$log\frac{p_{\theta (y|x)}}{p(y)}$在引入先验概率后,建模了什么与什么的互信息?这块还是没太理解,还是说这是实验得到的经验性结论暂时没有很好的指向
谢谢
建模了$x$与$y$的互信息,在分类问题上很明显$x$是输入、$y$是类别。既然你看到你说的那篇,那么就很清楚,互信息相比条件概率的好处就是排除了边缘分布的影响,学习到的关键往往更本质。
April 30th, 2023
作者你好,这里的prior是预先定义好的,我想如果设定prior为训练过程中各类别的采样数量,随训练进行而更新,是不是更应该符合prior的定义,我实验中我的想法没有效果,所以请问我的理解有什么问题,更普遍的一个问题是,有的时候因为训练集并不完全知晓其信息,所以不能先定义prior,这种情况应该怎么办
还有一个问题是对于posthoc,如果取一个极端的例子,A类有50000,B类只有1个,那posthoc感觉会对模型训练有害
太极端可能确实要另外考虑了。
prior的定义本身就是预先定好的,代表着我们对问题的一种先验认知,跟模型和训练过程无关。
如果prior随着训练更新,那大致上相当于引入了可训练的bias项,并且在测试过程中把bias项去掉,不知道你所说的没效果,在测试过程有没有把bias项去掉呢?
prior可以在训练过程中通过直接统计的方法逐步更新,也就是说,我们也许不能一次性获得所有训练集,但每次获得一个batch的训练集中,就用一个batch的label分布进行更新。跟直接引入bias的区别是bias项的更新规则不同,一个是用梯度下降更新,一个是直接根据统计规则更新。
May 16th, 2023
感谢苏神的回复,我还不明白用batch分布和整体分布设定prior的关系。由于当每个batch的分布都恰好与整体分布相同时,prior的两种设定完全等价,即按整体分布设定prior是按batch分布设定prior的一个极端特例,实际中batchsize越小那么两者的差别越明显。我后来在双月数据集上试了一下,batchsize设定为5,在多种不平衡条件下,prior设定为每个batch的分布时都略优于prior设定为整体分布的结果,与不用logits adjustment的baseline互有胜负,虽然这个实验太简单了不够有说服力,也能说明batch分布在一定程度下可行。我最大的问题是从理论不能理解这两种更新规则的关系,每个batch分布都是不同的,batchsize小的时候尤为明显,这种变化剧烈的prior直觉上总觉得会对训练有害,也应该与固定为整体分布的prior差别很大,但是效果还不错,我不明白为什么,请问苏神这两种方法理论上是等价的吗
所有batch的分布平均,是不是就等于总体分布呢?这更新规则,不能写成一个递归吗?
如果还不理解,看看 https://kexue.fm/archives/8069 的公式$(7),(8)$。
明白了,非常感谢
不好意思我还有一个问题,我看到有论文提到重采样、重加权、logits adjustment会冲突但没解释原因,是不是就是因为重采样相当于改变了整体的分布,要用logits adjustment也得重新设置prior;重加权和logits adjustment冲突可能是因为重加权改变了梯度,但这样是不是意味着prior的设置应该是各类别梯度的累计而不是单纯的采样数量呢
https://ieeexplore.ieee.org/document/10105457/
每一种方法的假设都是类别不均衡,当你用了某种方法之后,某种程度上已经解决了类别不均衡问题,此时再叠加另一种方法已经不满足假设了。至于具体细节,我没有分析,可能跟你说的差不多。
December 3rd, 2024
醍醐灌顶,原来数据不均衡的最优解早就有了,我还在傻傻的调权重,作者的文章比英文论文好懂很多,对我这种读原英文论文很吃力的人非常友好,而且循序渐进。
看第一遍一直在思考到底为啥让少的类别还更进一步的减少logit的值,那预测不是更不容易识别到,后面再仔细看发现原来训练和预测loss是不同的。
第二遍看到了加红的字:“能靠先验解决的就靠先验解决,先验解决不了的本质部分才由模型解决”。外加预测时公式9,明白过来了。
训练时,模型因为这个偏置项,多的类别模型可以相对更轻松识别到,而少的类别,需要把logit输出的很大才能突破偏置项的负面buff。相当于样本少的类别负重训练,而相反样本多的类别减轻训练强度。
预测时,去掉负重,自然对样本少的类别识别的会更均衡。(例子可能不恰当,我其实也是在总结我的思考,写给自己看的,哈哈)
感觉单标签多分类的数据不均衡问题这是最优解了。
很棒的文章。再次感谢作者,