科学空间|Scientific Spaces

前两周又在群里看到一个颇为有趣的问题：两个同样大小的椭圆片可以沿着它们的长轴弯曲，沿着边缘线粘贴，能完美地贴合成一个封闭立体吗？问题来源于知乎《两个椭圆片可否以柱面弯曲边缘完美贴合？》。

两个椭圆片粘合图示（截取自知乎上提问的图示）

问题可以用只言片语表达清楚，甚至普通读者都能理解，而问题本身是有一定难度的，这就符合了一个漂亮的问题的条件，所以也就吸引了笔者陆陆续续思考了好多天，最终在昨天算是给出了这类问题通用的列方程思路和数值求解方案，而今天则完成了理论证明，确认两个相同椭圆片总是可以完美贴合。

点击阅读全文...

在文章《玩转Keras之seq2seq自动生成标题》中我们已经基本探讨过seq2seq，并且给出了参考的Keras实现。

本文则将这个seq2seq再往前推一步，引入双向的解码机制，它在一定程度上能提高生成文本的质量（尤其是生成较长文本时）。本文所介绍的双向解码机制参考自《Synchronous Bidirectional Neural Machine Translation》，最后笔者也是用Keras实现的。

背景介绍

研究过seq2seq的读者都知道，常见的seq2seq的解码过程是从左往右逐字（词）生成的，即根据encoder的结果先生成第一个字；然后根据encoder的结果以及已经生成的第一个字，来去生成第二个字；再根据encoder的结果和前两个字，来生成第三个词；依此类推。总的来说，就是在建模如下概率分解
\begin{equation}p(Y|X)=p(y_1|X)p(y_2|X,y_1)p(y_3|X,y_1,y_2)\cdots\label{eq:p}\end{equation}

点击阅读全文...

（注：本文的相关内容已整理成论文《ZLPR: A Novel Loss for Multi-label Classification》，如需引用可以直接引用英文论文，谢谢。）

一般来说，在处理常规的多分类问题时，我们会在模型的最后用一个全连接层输出每个类的分数，然后用softmax激活并用交叉熵作为损失函数。在这篇文章里，我们尝试将“Softmax+交叉熵”方案推广到多标签分类场景，希望能得到用于多标签分类任务的、不需要特别调整类权重和阈值的loss。

类别不平衡

单标签到多标签

一般来说，多分类问题指的就是单标签分类问题，即从$n$个候选类别中选$1$个目标类别。假设各个类的得分分别为$s_1,s_2,
\dots,s_n$，目标类为$t\in\{1,2,\dots,n\}$，那么所用的loss为
\begin{equation}-\log \frac{e^{s_t}}{\sum\limits_{i=1}^n e^{s_i}}= - s_t + \log \sum\limits_{i=1}^n e^{s_i}\label{eq:log-softmax}\end{equation}
这个loss的优化方向是让目标类的得分$s_t$变为$s_1,s_2,\dots,s_t$中的最大值。关于softmax的相关内容，还可以参考《寻求一个光滑的最大值函数》、《函数光滑化杂谈：不可导函数的可导逼近》等文章。

点击阅读全文...

在NLP中，我们经常要去比较两个句子的相似度，其标准方法是想办法将句子编码为固定大小的向量，然后用某种几何距离（欧氏距离、$\cos$距离等）作为相似度。这种方案相对来说比较简单，而且检索起来比较快速，一定程度上能满足工程需求。

此外，还可以直接比较两个变长序列的差异性，比如编辑距离，它通过动态规划找出两个字符串之间的最优映射，然后算不匹配程度；现在我们还有Word2Vec、BERT等工具，可以将文本序列转换为对应的向量序列，所以也可以直接比较这两个向量序列的差异，而不是先将向量序列弄成单个向量。

后一种方案速度相对慢一点，但可以比较得更精细一些，并且理论比较优雅，所以也有一定的应用场景。本文就来简单介绍一下属于后者的两个相似度指标，分别简称为WMD、WRD。

Earth Mover's Distance

本文要介绍的两个指标都是以Wasserstein距离为基础，这里会先对它做一个简单的介绍，相关内容也可以阅读笔者旧作《从Wasserstein距离、对偶理论到WGAN》。Wasserstein距离也被形象地称之为“推土机距离”（Earth Mover's Distance，EMD），因为它可以用一个“推土”的例子来通俗地表达它的含义。

点击阅读全文...

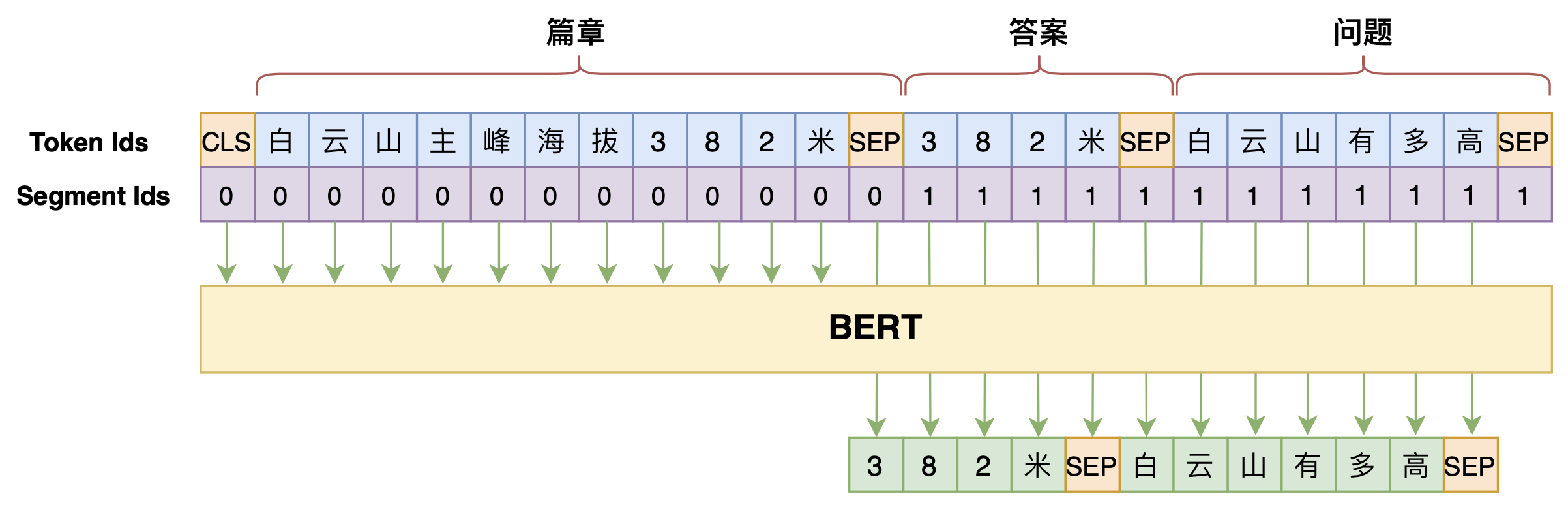
机器阅读理解任务，相比不少读者都有所了解了，简单来说就是从给定篇章中寻找给定问题的答案，即“篇章 + 问题 → 答案”这样的流程，笔者之前也写过一些关于阅读理解的文章，比如《基于CNN的阅读理解式问答模型：DGCNN》等。至于问答对构建，则相当于是阅读理解的反任务，即“篇章 → 答案 + 问题”的流程，学术上一般直接叫“问题生成（Question Generation）”，因为大多数情况下，答案可以通过比较规则的随机选择，所以很多文章都只关心“篇章 + 答案 → 问题”这一步。

本文将带来一次全端到端的“篇章 → 答案 + 问题”实践，包括模型介绍以及基于bert4keras的实现代码，欢迎读者尝试。

本文的问答生成模型示意图

点击阅读全文...

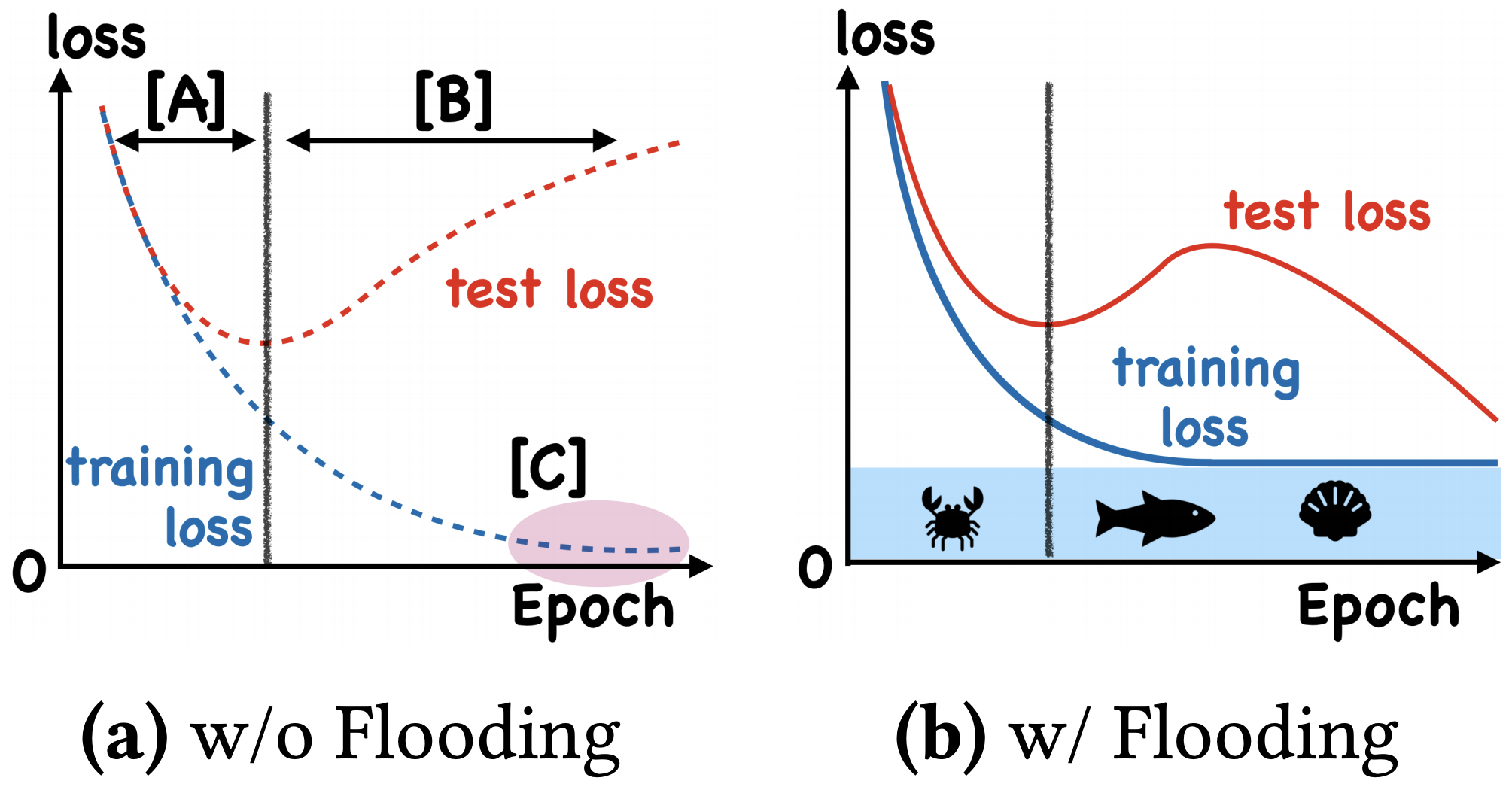
在训练模型的时候，我们需要损失函数一直训练到0吗？显然不用。一般来说，我们是用训练集来训练模型，但希望的是验证集的损失越小越好，而正常来说训练集的损失降低到一定值后，验证集的损失就会开始上升，因此没必要把训练集的损失降低到0。

既然如此，在已经达到了某个阈值之后，我们可不可以做点别的事情来提升模型性能呢？ICML 2020的论文《Do We Need Zero Training Loss After Achieving Zero Training Error?》回答了这个问题。不过论文的回答也仅局限在“是什么”这个层面上，并没很好地描述“为什么”，另外看了知乎上kid丶大佬的解读，也没找到自己想要的答案。因此自己分析了一下，记录在此。

左图：不加Flooding的训练示意图；右图：加了Flooding的训练示意图

点击阅读全文...

最近一段时间入了水族的坑，整了个60cm×40cm的超白缸来玩，主要是龟鱼共养。个人比较追求自然仿生，所以希望能在缸里建立一个相对稳定的仿生态环境。当然，其实这都是借口，根本原因是懒得换水，也不想洗过滤棉，所以就想着依靠生态系统自身的净化能力来延长换水时间。为此，参考网上的资料搞了个同程底滤，并且根据自己的经验做了一些修改。

生态缸-俯视图

点击阅读全文...

在机器学习中，我们经常会碰到不光滑的函数，但我们的优化方法通常是基于梯度的，这意味着光滑的模型可能更利于优化（梯度是连续的），所以就有了寻找非光滑函数的光滑近似的需求。事实上，本博客已经多次讨论过相关主题，比如《寻求一个光滑的最大值函数》、《函数光滑化杂谈：不可导函数的可导逼近》等，但以往的讨论在方法上并没有什么通用性。

不过，笔者从最近的一篇论文《SAU: Smooth activation function using convolution with approximate identities》学习到了一种比较通用的思路：用狄拉克函数来构造光滑近似。通用到什么程度呢？理论上有可数个间断点的函数都可以用它来构造光滑近似！个人感觉还是非常有意思的。

点击阅读全文...