科学空间|Scientific Spaces

在《VQ的旋转技巧：梯度直通估计的一般推广》中，我们介绍了VQ（Vector Quantization）的Rotation Trick，它的思想是通过推广VQ的STE（Straight-Through Estimator）来为VQ设计更好的梯度，从而缓解VQ的编码表坍缩、编码表利用率低等问题。

无独有偶，昨天发布在arXiv上的论文《Addressing Representation Collapse in Vector Quantized Models with One Linear Layer》提出了改善VQ的另一个技巧：给编码表加一个线性变换。这个技巧单纯改变了编码表的参数化方式，不改变VQ背后的理论框架，但实测效果非常优异，称得上是简单有效的经典案例。

点击阅读全文...

上一篇文章《当Batch Size增大时，学习率该如何随之变化？》我们从多个角度讨论了学习率与Batch Size之间的缩放规律，其中对于Adam优化器我们采用了SignSGD近似，这是分析Adam优化器常用的手段。那么一个很自然的问题就是：用SignSGD来近似Adam究竟有多科学呢？

我们知道，Adam优化器的更新量分母会带有一个$\epsilon$，初衷是预防除零错误，所以其值通常很接近于零，以至于我们做理论分析的时候通常选择忽略掉它。然而，当前LLM的训练尤其是低精度训练，我们往往会选择偏大的$\epsilon$，这导致在训练的中、后期$\epsilon$往往已经超过梯度平方大小，所以$\epsilon$的存在事实上已经不可忽略。

因此，这篇文章我们试图探索$\epsilon$如何影响Adam的学习率与Batch Size的Scaling Law，为相关问题提供一个参考的计算方案。

点击阅读全文...

继续回到我们的扩散系列。在《生成扩散模型漫谈（二十五）：基于恒等式的蒸馏（上）》中，我们介绍了SiD（Score identity Distillation），这是一种不需要真实数据、也不需要从教师模型采样的扩散模型蒸馏方案，其形式类似GAN，但有着比GAN更好的训练稳定性。

SiD的核心是通过恒等变换来为学生模型构建更好的损失函数，这一点是开创性的，同时也遗留了一些问题。比如，SiD对损失函数的恒等变换是不完全的，如果完全变换会如何？如何从理论上解释SiD引入的$\lambda$的必要性？上个月放出的《Flow Generator Matching》（简称FGM）成功从更本质的梯度角度解释了$\lambda=0.5$的选择，而受到FGM启发，笔者则进一步发现了$\lambda = 1$的一种解释。

接下来我们将详细介绍SiD的上述理论进展。

点击阅读全文...

这篇文章我们再次聚焦于扩散模型的采样加速。众所周知，扩散模型的采样加速主要有两种思路，一是开发更高效的求解器，二是事后蒸馏。然而，据笔者观察，除了上两篇文章介绍过的SiD外，这两种方案都鲜有能将生成步数降低到一步的结果。虽然SiD能做到单步生成，但它需要额外的蒸馏成本，并且蒸馏过程中用到了类似GAN的交替训练过程，总让人感觉差点意思。

本文要介绍的是《One Step Diffusion via Shortcut Models》，其突破性思想是将生成步长也作为扩散模型的条件输入，然后往训练目标中加入了一个直观的正则项，这样就能直接稳定训练出可以单步生成模型，可谓简单有效的经典之作。

ODE扩散

原论文的结论是基于ODE式扩散模型的，而对于ODE式扩散的理论基础，我们在本系列的（六）、（十二）、（十四）、（十五）、（十七）等博客中已经多次介绍，其中最简单的一种理解方式大概是（十七）中的ReFlow视角，下面我们简单重复一下。

点击阅读全文...

宇宙中存在所谓的“黑洞”，只要你步入了它的视界之内，就永远也出不去了（除非你能够超光速）。在数学中，也有类似的规则，只要把一个自然数代入这个规则，都无一不会陷入无限的循环之中，这样称之为“数字黑洞”。有一个“数字黑洞”，它令人十分着迷，甚至有人称它为“企图减缓美国数学进展的阴谋”——这就是“冰雹猜想”。

冰雹猜想：
任选一个自然数。当选定的自然数是偶数，将它除以2，如是奇数，将它乘以3加上1；当变换后的自然数成了偶数，再将它除以2，如成了奇数，再将它乘以3加上1，连续进行下去，最后都“落叶归根”——变成了1。

点击阅读全文...

A,B,C,D四人做10道回答是否的问题，答对了得一分，四人的答案和A,B,C的得分如图所示。问D的得分是多少？（附加说明：这里的答错不扣分）

事实上，这道题目本身已经把难度降到非常低了，因此推荐大家都去想一下。
如果你实在没有心思去想，可以直接看答案（不推荐）。

点击阅读全文...

本证明是站长经过很长时间独立研究得出，望转载者要注明原作者和出处，否则定追究版权责任！ （公式很多，推荐使用火狐浏览器）

关于这个不等式由来已久，从$\frac{a+b}{2} \geq \sqrt{ab}$开始，人们逐渐地发现，只要$a_1,a_2,...,a_n \geq 0$，那么就一定会有$\frac{a_1+a_2+...+a_n}{n} \geq \sqrt[n]{a_1 a_2...a_n}$。对于比较小的n，人们已经可以证明上式成立，但是，一般形式的证明则是近年来的事情。

我自己很早就接触到了这个不等式（好像是3年前，我读六年级），从那个时候开始，我就一直寻找这个不等式的证明，但是除了n=2的情况外，其余一直未果。直到三个月前的一节数学课，在发愣之余就想出来了(^_^)。一开始证明了n=3的情况，然后就势如破竹，证明了对于任何的n，这条不等式都成立。

点击阅读全文...

201002150000星空图

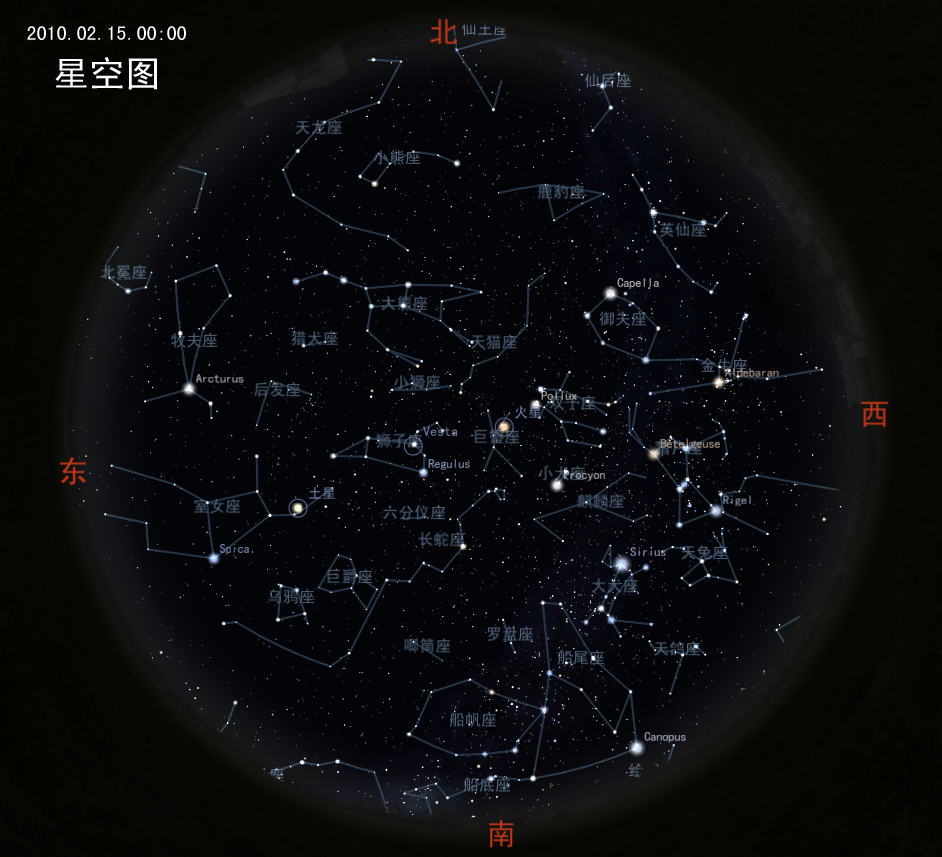
精彩天象不断的一月刚刚过去，我们迎来了夜空相对寂寥的2月。对于我们来说，本月是今年天象最少的一个月。尽管如此，我们依旧十分喜庆——本月14日，是我国传统的新春佳节，在此科学空间祝大家新年快乐、工作顺利、生活愉快！

春节期间有几个月光干扰较少的暗夜。近几年不少城里人都喜欢在春节期间到乡村去体验更浓的年味，如果天气晴朗，晚上正好有机会可以看看美丽的星空，过一个欢乐而有意义的长假。 站长也是农村里的孩子，欢迎各位同好来访，站长定会招待。不过今年将近过了一个月了，我只看到过一晚的星星，其余的不是阴天就是下雨，太阳也没有见到几回。因此，欢迎大家来贺新年！

点击阅读全文...