科学空间|Scientific Spaces

这个系列慢慢写到第7篇，基本上也把分词的各种模型理清楚了，除了一些细微的调整（比如最后的分类器换成CRF）外，剩下的就看怎么玩了。基本上来说，要速度，就用基于词典的分词，要较好地解决组合歧义何和新词识别，则用复杂模型，比如之前介绍的LSTM、FCN都可以。但问题是，用深度学习训练分词器，需要标注语料，这费时费力，仅有的公开的几个标注语料，又不可能赶得上时效，比如，几乎没有哪几个公开的分词系统能够正确切分出“扫描二维码，关注微信号”来。

本文就是做了这样的一个实验，仅用一个词典，就完成了一个深度学习分词器的训练，居然效果还不错！这种方案可以称得上是半监督的，甚至是无监督的。

点击阅读全文...

魏尔斯特拉斯定理

将狄拉克函数理解为函数的极限，可以衍生出很丰富的内容，而且这些内容离严格的证明并不遥远。比如，定义
$$\delta_n(x)=\left\{\begin{aligned}&\frac{(1-x^2)^n}{I_n},x\in[-1,1]\\
&0,\text{其它情形}\end{aligned}\right.$$
其中$I_n = \int_{-1}^1 (1-x^2)^n dx$，于是不难证明
$$\delta(x)=\lim_{n\to\infty}\delta_n(x)$$
这样，对于$[a,b]$上的连续函数$f(x)$，我们就得到
$$f(x)=\int_{-1}^1 f(y)\delta(x-y)dy = \lim_{n\to\infty}\int_{-1}^1 f(y)\delta_n(x-y) dy$$
这里$-1 < a < b < 1$，并且我们已经“不严谨”地交换了积分号和极限号，但这不是特别重要。重要的是它的结果：可以看到
$$P_n(x)=\int_{-1}^1 f(y)\delta_n(x-y) dy$$
是$x$的一个$2n$次多项式，因此上式表明$f(x)$是一个$2n$次的多项式的极限！这就引出了著名的“魏尔斯特拉斯定理”：

闭区间上的连续函数都可以用多项式一致地逼近。

点击阅读全文...

咋看上去，SVD分解是比较传统的数据挖掘手段，自编码器是深度学习中一个比较“先进”的概念，应该没啥交集才对。而本文则要说，如果不考虑激活函数，那么两者将是等价的。进一步的思考就可以发现，不管是SVD还是自编码器，我们降维，并不是纯粹地为了减少储存量或者减少计算量，而是“智能”的初步体现。

等价性

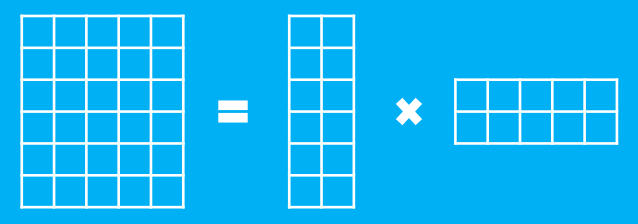
假设有一个$m$行$n$列的庞大矩阵$M_{m\times n}$，这可能使得计算甚至存储上都成问题，于是考虑一个分解，希望找到矩阵$A_{m\times k}$和$B_{k\times n}$，使得
$$M_{m\times n}=A_{m\times k}\times B_{k\times n}$$
这里的乘法是矩阵乘法。如图

SVD

点击阅读全文...

提前祝各位读者新年快乐，2017行好运～

这篇文章主要想回答两个“为什么”的问题：1、为啥我就对SVD感兴趣了？；2、为啥我说SVD是一个聚类过程？回答的内容纯粹个人思辨结果，暂无参考文献。

为什么要研究SVD？

从2015年接触深度学习到现在，已经研究了快两年的深度学习了，现在深度学习、数据科学等概念也遍地开花。为什么在深度学习火起来的时候，我反而要回去研究“古老”的SVD分解呢？我觉得，SVD作为一个矩阵分解算法，它的价值不仅仅体现在它广泛的应用，它背后还有更加深刻的内涵，即它的可解释性。在深度学习流行的今天，不少人还是觉得深度学习（神经网络）就是一个有效的“黑箱”模型。但是，仅用“黑箱”二字来解释深度学习的有效性显然不能让人满意。前面已经说过，SVD分解本质上与不带激活函数的三层自编码机等价，理解SVD分解，能够为神经网络模型寻求一个合理的概率解释。

点击阅读全文...

如果依次阅读该系列文章的读者，就会发现这个系列共提供了两种从0到1的无监督分词方案，第一种就是《【中文分词系列】 2. 基于切分的新词发现》，利用相邻字凝固度（互信息）来做构建词库（有了词库，就可以用词典法分词）；另外一种是《【中文分词系列】 5. 基于语言模型的无监督分词》，后者基本上可以说是提供了一种完整的独立于其它文献的无监督分词方法。

但总的来看，总感觉前面一种很快很爽，却又显得粗糙；后面一种很好很强大，却又显得太过复杂（viterbi是瓶颈之一）。有没有可能在两者之间折中一下？这就导致了本文的结果，达到了速度与效果的平衡。至于为什么说“更好”？因为笔者研究词库构建也有一段时间了，以往构建的词库总不能让人（让自己）满意，生成的词库一眼看上去，都能够扫到不少不合理的地方，真的要用得需要经过较多的人工筛选。而这一次，一次性生成的词库，一眼扫过去，不合理的地方少了很多，如果不细看，可能就发现不了了。

分词的目的

点击阅读全文...

文本情感分类其实就是一个二分类问题，事实上，对于分类模型，都会存在这样一个毛病：优化目标跟考核指标不一致。通常来说，对于分类（包括多分类），我们都会采用交叉熵作为损失函数，它的来源就是最大似然估计（参考《梯度下降和EM算法：系出同源，一脉相承》）。但是，我们最后的评估目标，并非要看交叉熵有多小，而是看模型的准确率。一般来说，交叉熵很小，准确率也会很高，但这个关系并非必然的。

要平均，不一定要拔尖

一个更通俗的例子是：一个数学老师，在努力提高同学们的平均分，但期末考核的指标却是及格率（60分及格）。假如平均分是100分（也就意味着所有同学都考到了100分），那么自然及格率是100%，这是最理想的。但现实不一定这么美好，平均分越高，只要平均分还没有达到100，那么及格率却不一定越高，比如两个人分别考40和90，那么平均分就是65，及格率只有50%；如果两个人的成绩都是60，平均分就是60，及格率却有100%。这也就是说，平均分可以作为一个目标，但这个目标并不直接跟考核目标挂钩。

那么，为了提升最后的考核目标，这个老师应该怎么做呢？很显然，首先看看所有学生中，哪些同学已经及格了，及格的同学先不管他们，而针对不及格的同学进行补课加强，这样一来，原则上来说有很多不及格的同学都能考上60分了，也有可能一些本来及格的同学考不够60分了，但这个过程可以迭代，最终使得大家都在60分以上，当然，最终的平均分不一定很高，但没办法，谁叫考核目标是及格率呢？

点击阅读全文...

PS：本文就是梳理了梯度下降与EM算法的关系，通过同一种思路，推导了普通的梯度下降法、pLSA中的EM算法、K-Means中的EM算法，以此表明它们基本都是同一个东西的不同方面，所谓“横看成岭侧成峰，远近高低各不同”罢了。

在机器学习中，通常都会将我们所要求解的问题表示为一个带有未知参数的损失函数(Loss)，如平均平方误差（MSE），然后想办法求解这个函数的最小值，来得到最佳的参数值，从而完成建模。因将函数乘以-1后，最大值也就变成了最小值，因此一律归为最小值来说。如何求函数的最小值，在机器学习领域里，一般会流传两个大的方向：1、梯度下降；2、EM算法，也就是最大期望算法，一般用于复杂的最大似然问题的求解。

在通常的教程中，会将这两个方法描述得迥然不同，就像两大体系在分庭抗礼那样，而EM算法更是被描述得玄乎其玄的感觉。但事实上，这两个方法，都是同一个思路的不同例子而已，所谓“本是同根生”，它们就是一脉相承的东西。

让我们，先从远古的牛顿法谈起。

牛顿迭代法

给定一个复杂的非线性函数$f(x)$，希望求它的最小值，我们一般可以这样做，假定它足够光滑，那么它的最小值也就是它的极小值点，满足$f'(x_0)=0$，然后可以转化为求方程$f'(x)=0$的根了。非线性方程的根我们有个牛顿法，所以
\begin{equation}x_{n+1} = x_{n} - \frac{f'(x_n)}{f''(x_n)}\end{equation}

点击阅读全文...

对于了解深度学习、自然语言处理NLP的读者来说，Word2Vec可以说是家喻户晓的工具，尽管不是每一个人都用到了它，但应该大家都会听说过它——Google出品的高效率的获取词向量的工具。

Word2Vec不可思议？

大多数人都是将Word2Vec作为词向量的等价名词，也就是说，纯粹作为一个用来获取词向量的工具，关心模型本身的读者并不多。可能是因为模型过于简化了，所以大家觉得这样简化的模型肯定很不准确，所以没法用，但它的副产品词向量的质量反而还不错。没错，如果是作为语言模型来说，Word2Vec实在是太粗糙了。

但是，为什么要将它作为语言模型来看呢？抛开语言模型的思维约束，只看模型本身，我们就会发现，Word2Vec的两个模型 —— CBOW和Skip-Gram —— 实际上大有用途，它们从不同角度来描述了周围词与当前词的关系，而很多基本的NLP任务，都是建立在这个关系之上，如关键词抽取、逻辑推理等。这几篇文章就是希望能够抛砖引玉，通过介绍Word2Vec模型本身，以及几个看上去“不可思议”的用法，来提供一些研究此类问题的新思路。

点击阅读全文...