科学空间是2009年3月建立的，虽然其中经历了一些变动，但是从2009年下半年开始，科学空间就一直在“宇宙驿站”的怀抱之中健康成长着。今天，科学空间即将三岁了（03.16视为科学空间建立的日子），而宇宙驿站则已经十岁了。
在宇宙驿站中，崔博等许许多多人做出了不懈努力，为我们这些科学爱好者提供者免费而优越的服务，BoJone对此有无限的感激之情。与宇宙驿站有种相见恨晚的感觉，不过虽然没有经历建立之初那激动人心的时刻，但是，既然已经和驿站一起、和各位读者一起走了这么久了，就应该一直走下去。
谨此留念
By 崔辰州博士：
十年前的今天，2002年3月12日，在国家天文台LAMOST三楼的小机房里一台从中关村电子市场淘来的电脑对外开始了她的职业生涯，这就是最初的宇宙驿站。
生日祝福
2012年3月28日，我19岁了。
三月是一个很美的月份，我的很多值得纪念的日子都在三月发生，还有好友们都在三月接二连三地生日，几乎让我措手不及了，呵呵。我的同桌黄金，好友家益，还有我自己都在这个月成为十九岁的孩子了。算起来，我应该是“最年轻”的了^_^
3-25-聚餐合照
我的生日收到了许多人的祝福，这让我觉得很意外，我一直觉得，我不善于人际交往，所以不应该会有太多人关注我，但惊喜在我身上发生了。谢谢大家。
人生如梦，繁星流动，和你同路，从不相识开始心接近，默默以真挚待人......这是《朋友》的歌词，也是我们之间的真实写照。感谢上天，让我的人生之路上有你们的相伴，人生因为你们而更加精彩。愿能够与你们一起度过、奋斗过更多的日子！我们相约，我们是一辈子的朋友！
30
Apr
引力透镜——用经典力学推导光的偏转公式
By 苏剑林 | 2012-04-30 | 62159位读者 | 引用引力透镜
————用经典力学推导光的引力偏转角公式
引力透镜效应造成的爱因斯坦十字
在2012年第四期的《天文爱好者》上，Richard de Grijs（何锐思）教授的《引力透镜——再领科学潮》一文详细而精彩地讲述了有关引力透镜方面的知识，尤其是它在天文方面的重要应用，让我收获颇丰。笔者在赞叹作者优美的文笔和译者程思浩同好的生动翻译之余，也感到了一丝不足。文章主要讲了引力透镜在天文研究中所扮演的重要角色，却未对引力透镜的原理、本质方面多加描述。时空的扭曲是广义相对论给出的答案，可是难道仅仅从经典力学就不能领略丝毫？藉此，BoJone这在里对引力透镜多说些东西，与大家相互学习研究。当然，由于我只是一个初出茅庐的业余爱好者，其中的不当之处还望各位斧正。
1
May
相对论、对称和第四维
By 苏剑林 | 2012-05-01 | 77763位读者 | 引用这篇文章其实在年初就完成了。
众所周知，我们生活在一个平坦的世界中。正如我们能够感受到的那样，在这个被称为“欧几里得平直空间”的世界里，空间里两点间的最短曲线是两点间的直线段，空间里的任意直角三角形都满足勾股定理，每个物体都有着自己的长、宽、高，它们都随着时间的流逝而运动着。这种世界观把时间独立于空间之外，作为一个独特的研究对象。但是自爱因斯坦在1905年发表狭义相对论以来，我们的宇宙就被描述成为了由三维空间和一维时间组成的“四维时空”，在这里，时间和空间的地位是等价的。不少同好们也许会感到非常困惑：即使证明了时间与空间的确存在着某种联系，也不必要把时间描述成是世界的一维吧？在我们的感官里，时间明明就和空间的三维差别甚大，时间和空间怎么能够等同起来呢？其实答案很简单：为了美。把时间看成与空间等价的一维之后，整个力学体系体现出一种前所未有的对称美，这种美不仅让人赏心悦目，而且极大地方便了我们进一步处理问题。
对称
30
Jun
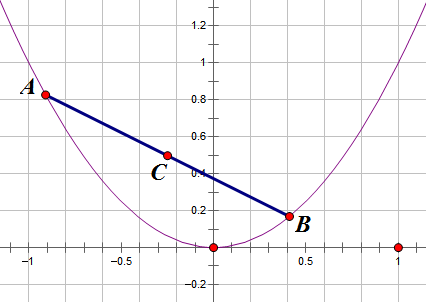
抛物线内一根定长的弦
By 苏剑林 | 2012-06-30 | 32326位读者 | 引用
6
Jul
椭圆内的一根定长弦（化圆法）
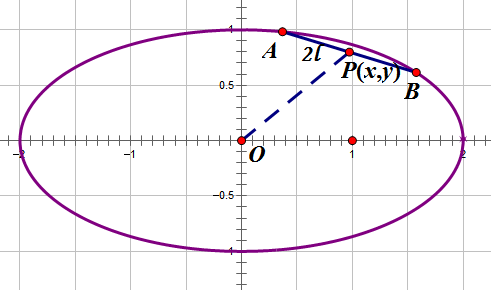
By 苏剑林 | 2012-07-06 | 30691位读者 | 引用在上一篇文章《抛物线内的一根定长弦》中，我们解决了抛物线内的定长弦中点轨迹问题，那还算是一个比较简单的问题。虽然同是圆锥曲线，但把同样的问题延伸到椭圆上，却不是那么简单了。因为椭圆的轨迹方程的x,y坐标通过平方相互“纠缠”在一起，不像抛物线方程那样可以容易分离开来（指的是分离成$y=f(x)$的形式）。BoJone尝试了若干种方法，还是难以把它的轨迹求出来。最后通过“化圆法”，终得轨迹方程。
椭圆内的定长弦1
所谓化圆法，就是将椭圆通过拉伸变成一个圆，利用圆的性质来解决一些问题。众所周知，相比椭圆，圆具有相当多的简单性。这是我高考前研究各种各样的高考圆锥曲线题时，所总结出来的一种方法。有时候，把椭圆拉伸为圆后，结论就相当显然了；同时，圆作为一个特殊的椭圆，椭圆的一般结论，放在圆上自然也是成立的。所以要研究椭圆问题，不妨先研究它的特例——圆问题；另一方面，利用圆的对称性等等，也可以大幅度地减少计算量，所以BoJone很喜欢这个方法。更想不到的是，它居然在求本文的轨迹时派上用场了。
最近评论