引力透镜——用经典力学推导光的偏转公式

引力透镜
————用经典力学推导光的引力偏转角公式

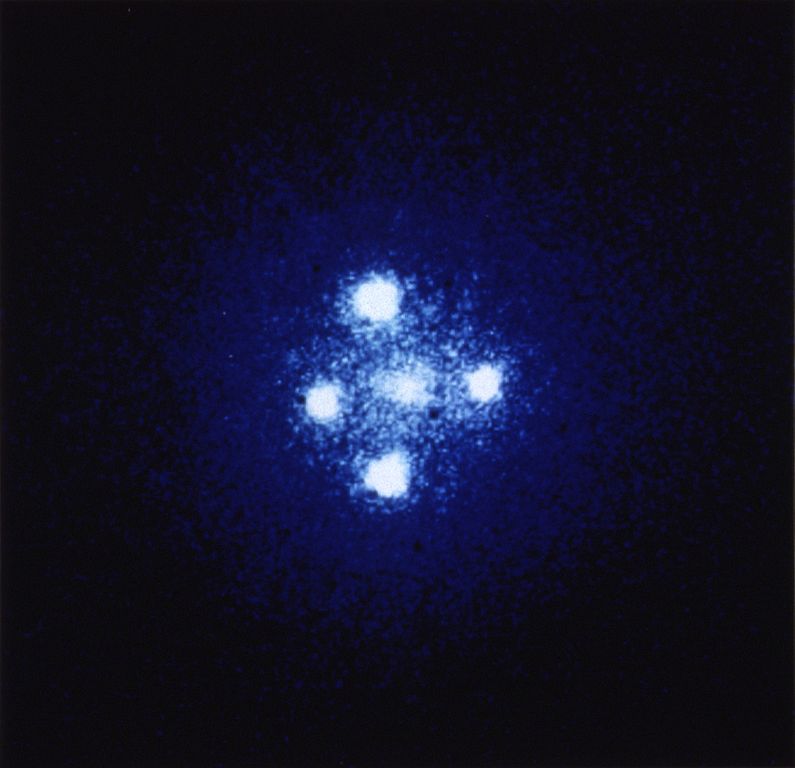
在2012年第四期的《天文爱好者》上，Richard de Grijs（何锐思）教授的《引力透镜——再领科学潮》一文详细而精彩地讲述了有关引力透镜方面的知识，尤其是它在天文方面的重要应用，让我收获颇丰。笔者在赞叹作者优美的文笔和译者程思浩同好的生动翻译之余，也感到了一丝不足。文章主要讲了引力透镜在天文研究中所扮演的重要角色，却未对引力透镜的原理、本质方面多加描述。时空的扭曲是广义相对论给出的答案，可是难道仅仅从经典力学就不能领略丝毫？藉此，BoJone这在里对引力透镜多说些东西，与大家相互学习研究。当然，由于我只是一个初出茅庐的业余爱好者，其中的不当之处还望各位斧正。

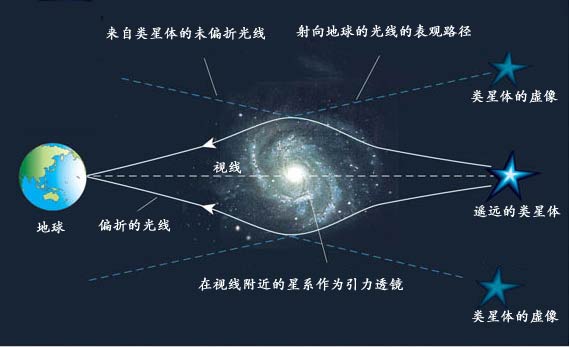
引力透镜成因 #

引力透镜是怎么产生的？当然是因为光在引力场中会偏折。可是光线好端端地有直路不走，为什么要走弯路呢？根据费马原理，光总是走用时尽可能少的路径去到达目的地^注*，要是走曲线，那不是违反这一原理了吗？通常我们会用广义相对论来回答：质量导致了时空维度的扭曲，使得空间两点间的最短距离不再是直线（就像地球表面上的两点间的最短距离是圆弧）。但广义相对论的说法是比较专业的，并不怎么直观。我们或许可以用经典理论来换一个角度思考这个问题。

平时光从透镜中会发生折射，是因为透镜具有大于1的折射率，这意味着什么呢？事实上这表明光在透镜中（玻璃）传播速度更慢。根据光学中的费马原理，它要走折线才能花最短的时间，这就导致了折射定律。“引力透镜”是否有类似原理呢？光在引力场中的速度变慢呢？在某种意义上是可以这样认为的，因为光在扭曲的高维时空中走了一条曲线，而在我们三维空间看来，它走的依然是直线，但是时间却变长了，所以看起来速度就变慢了，这等价于它有了一个时空的“折射率”，因此它就得走弯路了。^注**反过来，如果肯定“光在真空中速度不变”这一相对性原理，那么就可以得出“质量把时空扭曲了”这一结论，因为只有这一观点才能保持费马原理的正确性。这也是用引力透镜来检验广义相对论的原因。

另一方面，从经典力学的角度来讲，根据光子能量$E=h \nu$和质能方程$E=mc^2$可以得出$m=\frac{h\nu}{c^2}$ ，即光可以看成质量为$m=\frac{h\nu}{c^2}$的粒子。既然如此，粒子经过引力场受到引力作用当然会偏折了。这是天体力学中的“二体问题”^注***。令人意外的是，任何一个有一些天体力学基础的同好，都可以从这个角度出发，由经典天体力学的一些定律，加上一些不严谨的假设，来得出光在引力场中的偏转角公式。而且最不可思议的是，不严谨的结果与广义相对论的结果完全一致！当然这只是一个神奇的巧合，它并不严谨，但也有一定的欣赏价值。在这里与各位同好分享，也权当抛砖引玉。

经典力学：光在引力场的偏转角 #

光子的速度为c，这已经远远大于许多恒星的第二宇宙速度了，根据天体力学，光子经过这些恒星附近走的是双曲线了，恒星（太阳）位于双曲线的一个焦点上。由解析几何，对于任意一条双曲线，其方程为
$$\frac{x^2}{a^2}-\frac{y^2}{b^2} =1 $$

如何表示偏转角呢？我们可以考虑双曲线的两条渐近线：$\frac{y}{x} = \pm \frac{b}{a}$

如图，θ角的大小就是偏转角的大小，而且$\theta=2\varphi=2 \arctan\frac{a}{b}$ ，假设双曲线的离心率$e$非常大（光线在引力场正是这种情况，因为它的初速度为$c$，非常大），那么就有$a \ll b$，
$$\frac{a}{b}=\frac{a}{a\sqrt{e^2-1}} \approx \frac{1}{e} \approx 0$$

对于很小的角度$\theta$，有$\tan\theta\approx \theta$，所以有
$$\theta \approx 2 \arctan \frac{1}{e} \approx \frac{2}{e}$$

接下来的目标是求出e。天体力学中有一条重要的“活力公式”（这似乎是奥赛朋友们必懂的？）
$v^2=GM(\frac{2}{r}-\frac{1}{a})$ ，对于双曲线来说变成了$v^2=GM(\frac{2}{r}+\frac{1}{a})$ ，它描述了速度$v$随距离$r$的变化情况。当然光速不会变化，但是这里我们忽略这一情况，我们假设光到达“近日点”（图中的B点）时速度为c，那么就有$v=c$以及$r=a(e-1)\approx ae$了，代入活力公式就可以得出
$$c^2 = GM(\frac{e}{r}+\frac{2}{r}) = \frac{GM(e+2)}{r} \approx \frac{GMe}{r}$$

即$e \approx \frac{c^2 r}{GM} $，代入$\theta \approx \frac{2}{e}$得到
$$\theta \approx \frac{2GM}{c^2 r}$$
这广义相对论所给出结果的一半。可以说，要初步理解引力透镜，不一定需要广义相对论这个精深的理论。

再说一点 #

直接套用经典力学类比来理解和估计广义相对论所预测的现象，很多时候能得到合理的结果，有时候像由第二宇宙速度公式$v =\sqrt{\frac{2GM}{r}}$得出黑洞半径$r_g = \frac{2GM}{c^2}$一样，得到正确的估计公式，有时候会像前面所估算的一样，形式是对的，但差个比例。总之，基于光的“粒子性”，我们有可能借助经典力学初步理解一些比较深奥的理论结果。不过我对引力理论不了解，就不再多说些什么了。就单纯把过程放在这里，供大家参考。

上面是BoJone在看了《引力透镜——再领科学潮》一文后，心生兴趣而无意中的推算结果。我一直坚持“厚积厚发，薄积薄发”，拥有小小的知识也可以尽自己的力量去研究、分析天文物理现象，得出一些令人兴奋的结果，也许过程并不严谨、结果并不正确，这并不妨碍我们追逐天文的兴趣，相反，这是我们追逐天文之梦的动力和途径之一。

附加 #

*严格来讲，费马原理指的是光走的路径所需要的时间总是一个“极值”，有可能是极大值、极小值或者是恒定值，但是这里为了通俗描述，采取了一般的描述（最小值），这是在大多数情况下都成立的。

**可以想象一下，沿地球表面从南极匀速走到北极，而在外界看来我们只是从直线走到北极，那么外界看到的速度比我们的真实速度要慢。

***要想对“二体问题”有进一步的了解，在本blog搜索相关文章。

转载到请包括本文地址：https://spaces.ac.cn/archives/1592

更详细的转载事宜请参考：《科学空间FAQ》