科学空间|Scientific Spaces

本文是一次不怎么成功的半监督学习的尝试：在IMDB的数据集上，用随机抽取的1000个标注样本训练一个文本情感分类模型，并且在余下的49000个测试样本中，测试准确率为73.48%。

思路

本文的思路来源于OpenAI的这篇文章：
《OpenAI新研究发现无监督情感神经元：可直接调控生成文本的情感》

文章里边介绍了一种无监督（实际上是半监督）做情感分类的模型的方法，并且实验效果很好。然而文章里边的实验很庞大，对于个人来说几乎不可能重现（在4块Pascal GPU花了1个月时间训练）。不过，文章里边的思想是很简单的，根据里边的思想，我们可以做个“山寨版”的。思路如下：

我们一般用深度学习做情感分类，比较常规的思路就是Embedding层+LSTM层+Dense层(Sigmoid激活)，我们常说的词向量，相当于预训练了Embedding层（这一层的参数量最大，最容易过拟合），而OpenAI的思想就是，为啥不连LSTM层一并预训练了呢？预训练的方法也是用语言模型来训练。当然，为了使得预训练的结果不至于丢失情感信息，LSTM的隐藏层节点要大一些。

点击阅读全文...

列表

更别致的词向量模型(一)：simpler glove

更别致的词向量模型(二)：对语言进行建模

更别致的词向量模型(三)：描述相关的模型

更别致的词向量模型(四)：模型的求解

更别致的词向量模型(五)：有趣的结果

更别致的词向量模型(六)：代码、分享与结语

代码

本文的实现位于：https://github.com/bojone/simpler_glove

点击阅读全文...

发布

2018年01月30日

数目

共1千万条

格式

[
  {
    "url": "http://zhidao.baidu.com/question/565618371557484884.html",
    "question": "学文员有哪些专科学校",
    "tags": [
      "学校",
      "专科",
      "院校信息"
    ]
  },
  {
    "url": "http://zhidao.baidu.com/question/2079794100345438428.html",
    "question": "网赌和澳门赌有区别吗",
    "tags": [
      "网络",
      "澳门",
      "赌博"
    ]
  }
]

点击阅读全文...

前段时间天池出了个天文数据挖掘竞赛——LAMOST光谱分类（将对应的光谱识别为4类中的一类），虽然没有奖金，但还是觉得挺有意思，所以就报名参加了。做了一段时间，成绩自我感觉还可以，然而最后我却忘记了（或者说根本就没留意到）初赛最后两天还有一步是提交新的测试集结果，然后就没有然后了，留下了一个未竟的模型，可谓“出师未捷身先死”，还是被自己弄死的～

天文数据挖掘大赛——天体光谱智能分类

后来跟其他参赛选手讨论了一下，发现其实我的这个模型还是不错的。当时我记得初赛第一名的成绩是0.83+，而我当时的成绩是0.82+，排名大概是第4、5左右，而且据说很多分数在0.8+的队伍都已经使用了融合模型，而我这0.82+的成绩仅仅是单模型的结果～在平时的群聊中发现也有不少朋友在做一维序列分类模型，而光谱分类本质上也就是一个一维的序列分类，所以分享一下模型，估计对相关朋友会有一定的参考价值。

模型

事实上也不是什么特别的模型，就是普通的一维卷积加残差，对于熟悉图像处理的朋友，这实在是再普通不过的结构了。

点击阅读全文...

本文介绍来自MIT的一篇ICLR 2020满分论文《Why gradient clipping accelerates training: A theoretical justification for adaptivity》，顾名思义，这篇论文就是分析为什么梯度裁剪能加速深度学习的训练过程。原文很长，公式很多，还有不少研究复杂性的概念，说实话对笔者来说里边的大部分内容也是懵的，不过大概能捕捉到它的核心思想：引入了比常用的L约束更宽松的约束条件，从新的条件出发论证了梯度裁剪的必要性。本文就是来简明分析一下这个过程，供读者参考。

梯度裁剪

假设需要最小化的函数为$f(\theta)$，$\theta$就是优化参数，那么梯度下降的更新公式就是
\begin{equation}\theta \leftarrow \theta-\eta \nabla_{\theta} f(\theta)\end{equation}
其中$\eta$就是学习率。而所谓梯度裁剪（gradient clipping），就是根据梯度的模长来对更新量做一个缩放，比如
\begin{equation}\theta \leftarrow \theta- \eta \nabla_{\theta} f(\theta)\times \min\left\{1, \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert}\right\}\label{eq:clip-1}\end{equation}
或者
\begin{equation}\theta \leftarrow \theta- \eta \nabla_{\theta} f(\theta)\times \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert+\gamma}\label{eq:clip-2}\end{equation}
其中$\gamma > 0$是一个常数。这两种方式都被视为梯度裁剪，总的来说就是控制更新量的模长不超过一个常数，第二种形式也跟RMSProp等自适应学习率优化器相关。此外，更精确地，我们有下面的不等式
\begin{equation}\frac{1}{2}\min\left\{1, \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert}\right\}\leq \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert+\gamma}\leq \min\left\{1, \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert}\right\}\end{equation}
也就是说两者是可以相互控制的，所以其实两者基本是等价的。

点击阅读全文...

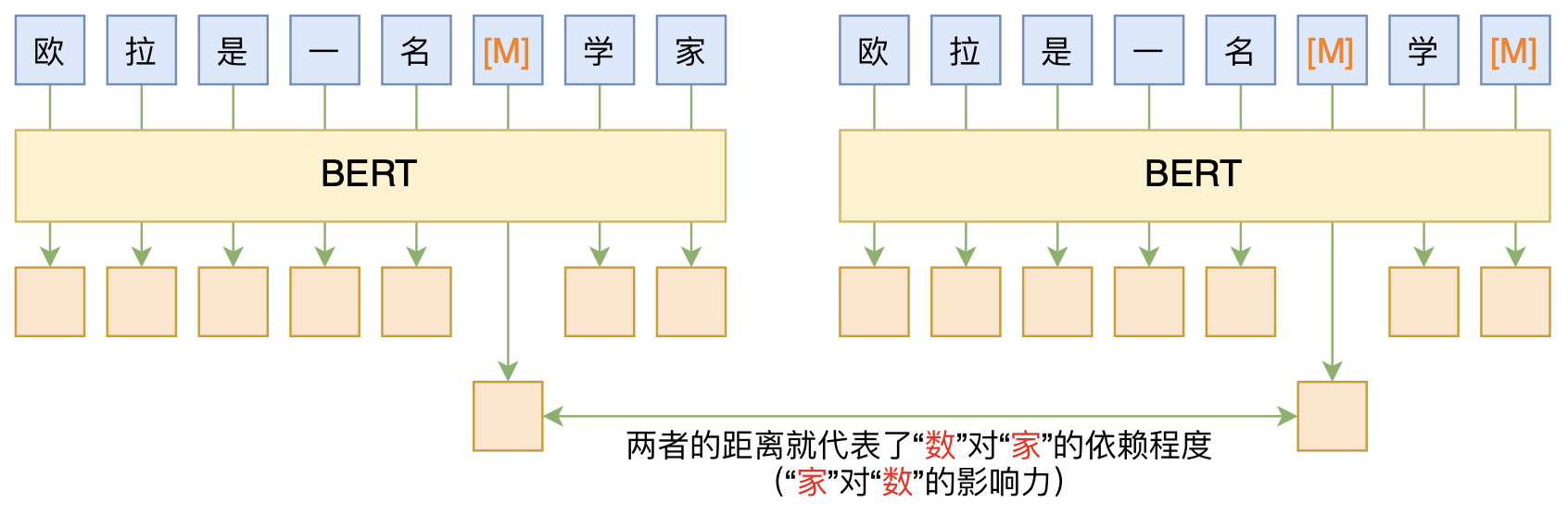
BERT的一般用法就是加载其预训练权重，再接一小部分新层，然后在下游任务上进行finetune，换句话说一般的用法都是有监督训练的。基于这个流程，我们可以做中文的分词、NER甚至句法分析，这些想必大家就算没做过也会有所听闻。但如果说直接从预训练的BERT（不finetune）就可以对句子进行分词，甚至析出其句法结构出来，那应该会让人感觉到意外和有趣了。

本文介绍ACL 2020的论文《Perturbed Masking: Parameter-free Probing for Analyzing and Interpreting BERT》，里边提供了直接利用Masked Language Model（MLM）来分析和解释BERT的思路，而利用这种思路，我们可以无监督地做到分词甚至句法分析。

基于BERT的“token-token”相关度计算图示

点击阅读全文...

去年笔者写过博文《如何应对Seq2Seq中的“根本停不下来”问题？》，里边介绍了一篇论文中对Seq2Seq解码不停止现象的处理，并指出那篇论文只是提了一些应对该问题的策略，并没有提供原理上的理解。近日，笔者在Arixv读到了AAAI 2021的一篇名为《A Theoretical Analysis of the Repetition Problem in Text Generation》的论文，里边从理论上分析了Seq2Seq重复解码现象。从本质上来看，重复解码和解码不停止其实都是同理的，所以这篇新论文算是填补了前面那篇论文的空白。

经过学习，笔者发现该论文确实有不少可圈可点之处，值得一读。笔者对原论文中的分析过程做了一些精简、修正和推广，将结果记录成此文，供大家参考。此外，抛开问题背景不讲，读者也可以将本文当成一节矩阵分析习题课，供大家复习线性代数哈～

点击阅读全文...

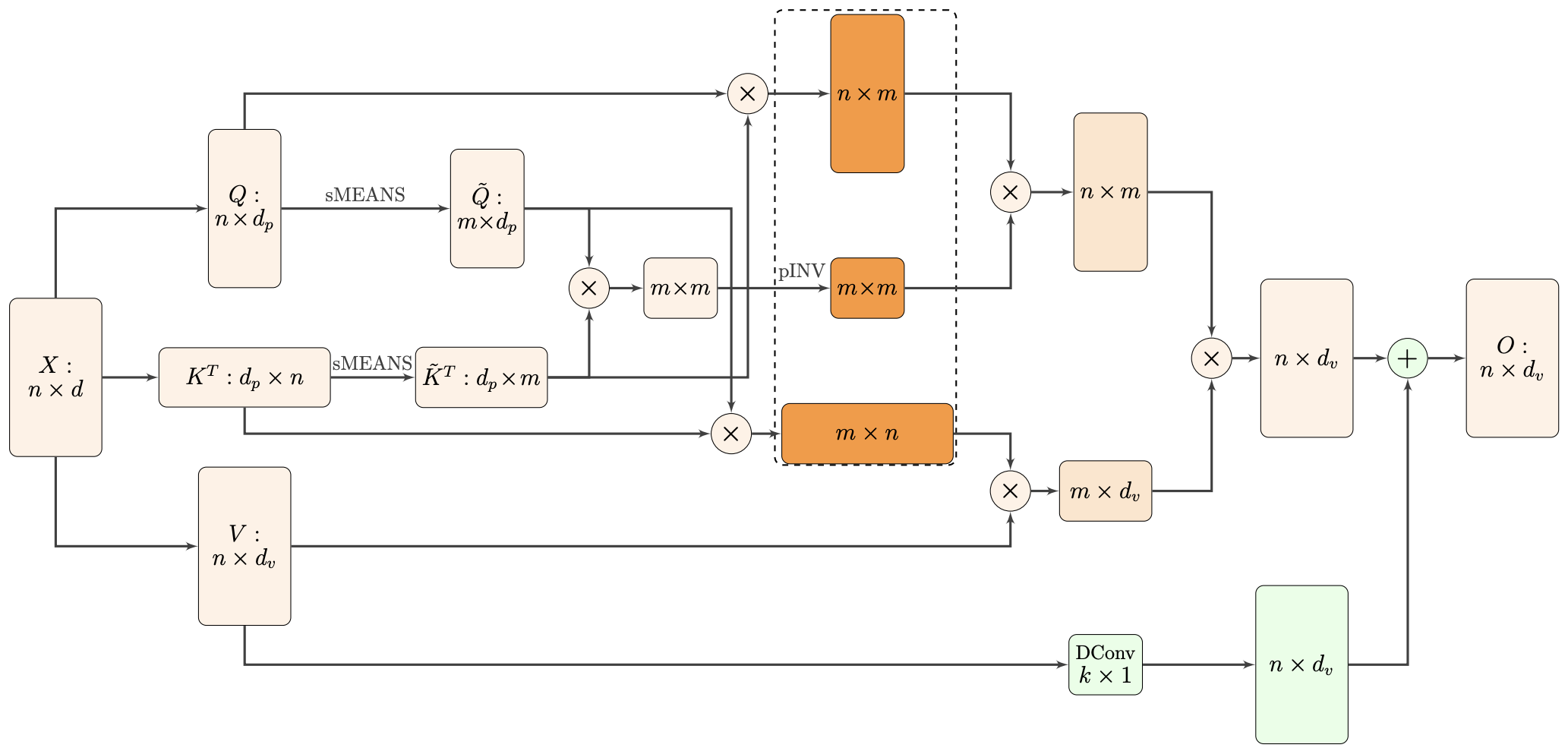
标准Attention的$\mathcal{O}(n^2)$复杂度可真是让研究人员头大。前段时间我们在博文《Performer：用随机投影将Attention的复杂度线性化》中介绍了Google的Performer模型，它通过随机投影的方式将标准Attention转化为线性Attention。无独有偶，前些天Arxiv上放出了AAAI 2021的一篇论文《Nyströmformer: A Nyström-Based Algorithm for Approximating Self-Attention》，里边又提出了一种从另一个角度把标准Attention线性化的方案。

Nyströmformer结构示意图

该方案写的是Nyström-Based，顾名思义是利用了Nyström方法来近似标准Attention的。但是坦白说，在看到这篇论文之前，笔者也完全没听说过Nyström方法，而纵观整篇论文，里边也全是笔者一眼看上去感觉很茫然的矩阵分解推导，理解起来颇为困难。不过有趣的是，尽管作者的推导很复杂，但笔者发现最终的结果可以通过一个相对来说更简明的方式来理解，遂将笔者对Nyströmformer的理解整理在此，供大家参考。

点击阅读全文...