OCR技术浅探:9. 代码共享(完)
By 苏剑林 | 2016-06-26 | 67894位读者 | 引用OCR技术浅探:8. 综合评估
By 苏剑林 | 2016-06-26 | 28930位读者 | 引用数据验证
尽管在测试环境下模型工作良好,但是实践是检验真理的唯一标准. 在本节中,我们通过自己的模型,与京东的测试数据进行比较验证.
衡量OCR系统的好坏有两部分内容:(1)是否成功地圈出了文字;(2)对于圈出来的文字,有没有成功识别. 我们采用评分的方法,对每一张图片的识别效果进行评分. 评分规则如下:
如果圈出的文字区域能够跟京东提供的检测样本的box文件中匹配,那么加1分,如果正确识别出文字来,另外加1分,最后每张图片的分数是前面总分除以文字总数.
按照这个规则,每张图片的评分最多是2分,最少是0分. 如果评分超过1,说明识别效果比较好了. 经过京东的测试数据比较,我们的模型平均评分大约是0.84,效果差强人意。
两个惊艳的python库:tqdm和retry
By 苏剑林 | 2016-08-13 | 65861位读者 | 引用Python基本是我目前工作、计算、数据挖掘的唯一编程语言(除了符号计算用Mathematica外)。当然,基本的Python功能并不是很强大,但它胜在有巨量的第三方扩展库。在选用Python的第三方库时,我都会经过仔细考虑,希望能挑选出最简单的、最直观的一个(因为本人比较笨,太复杂用不了)。在数据处理方面,我用得最多的是Numpy和Pandas,这两个绝对称得上王者级别的库,当然不能不提的是Scipy,但我很少直接用它,一般会通过Pandas间接调用了;可视化方面不用说是Matplotlib了;在建模方面,我会用Keras,直接上深度学习模型,Keras已经成为相当流行的深度学习框架了,如果做文本挖掘,通常还会用到jieba(分词)、Gensim(主题建模,包含了诸如word2vec之类的模型),机器学习库还有流行的Scikit Learn,但我很少用;网络方面,写爬虫我用requests,这是个人性化的网络库,如果写网站,我会用bottle,这是个单文件版的迷你框架,一切由自己定义,当然,我也不会去写什么大型网站,我就写一个简单的的接口那样而已;最后如果要并行的话,一般直接用multiprocessing。
不过,以上都不是本文要推荐的,本文要推荐的是两个可以渗透到日常写代码的库,它实现了我们平时很多时候都需要的功能,但是不用增加什么代码,绝对让人眼前一亮。
【中文分词系列】 2. 基于切分的新词发现
By 苏剑林 | 2016-08-18 | 122676位读者 | 引用上一篇文章讲的是基于词典和AC自动机的快速分词。基于词典的分词有一个明显的优点,就是便于维护,容易适应领域。如果迁移到新的领域,那么只需要添加对应的领域新词,就可以实现较好地分词。当然,好的、适应领域的词典是否容易获得,这还得具体情况具体分析。本文要讨论的就是新词发现这一部分的内容。
这部分内容在去年的文章《新词发现的信息熵方法与实现》已经讨论过了,算法是来源于matrix67的文章《互联网时代的社会语言学:基于SNS的文本数据挖掘》。在那篇文章中,主要利用了三个指标——频数、凝固度(取对数之后就是我们所说的互信息熵)、自由度(边界熵)——来判断一个片段是否成词。如果真的动手去实现过这个算法的话,那么会发现有一系列的难度。首先,为了得到$n$字词,就需要找出$1\sim n$字的切片,然后分别做计算,这对于$n$比较大时,是件痛苦的时间;其次,最最痛苦的事情是边界熵的计算,边界熵要对每一个片段就行分组统计,然后再计算,这个工作量的很大的。本文提供了一种方案,可以使得新词发现的计算量大大降低。
【中文分词系列】 3. 字标注法与HMM模型
By 苏剑林 | 2016-08-19 | 83881位读者 | 引用在这篇文章中,我们暂停查词典方法的介绍,转而介绍字标注的方法。前面已经提到过,字标注是通过给句子中每个字打上标签的思路来进行分词,比如之前提到过的,通过4标签来进行标注(single,单字成词;begin,多字词的开头;middle,三字以上词语的中间部分;end,多字词的结尾。均只取第一个字母。),这样,“为人民服务”就可以标注为“sbebe”了。4标注不是唯一的标注方式,类似地还有6标注,理论上来说,标注越多会越精细,理论上来说效果也越好,但标注太多也可能存在样本不足的问题,一般常用的就是4标注和6标注。
值得一提的是,这种通过给每个字打标签、进而将问题转化为序列到序列的学习,不仅仅是一种分词方法,还是一种解决大量自然语言问题的思路,比如命名实体识别等任务,同样可以用标注的方法来做。回到分词来,通过字标注法来进行分词的模型有隐马尔科夫模型(HMM)、最大熵模型(ME)、条件随机场模型(CRF),它们在精度上都是递增的,据说目前公开评测中分词效果最好的是4标注的CRF。然而,在本文中,我们要讲解的是最不精确的HMM。因为在我看来,它并非一个特定的模型,而是解决一大类问题的通用思想,一种简化问题的学问。
这一切,还得从概率模型谈起。
进驻中山大学南校区,折腾校园网
By 苏剑林 | 2016-09-05 | 78530位读者 | 引用开始研究僧之旅,希望有一天能企及扫地僧的境界。
进入中山大学后,各种郁闷的事情就来了。首先最郁闷的就是开学时间特早,8月26日开学,感觉至少比一般学校早了一星期,开学这么早有意思么~~接着就是感觉中大的管理制度各种混乱,比我本科的华师差多了。好吧,这些琐事先不吐槽,接下来弄校园网,这是作死的开始。
我们是在南校区的,校园网是通过锐捷客户端来认证的,而我是用macbook的,不过中大这边还很人性化地提供了Mac版的锐捷,体积就1M左右,挺好的。但众所周知,macbook并没有有线网卡,每次我上网都得插着个USB网卡然后连着网线,这该有多郁闷。于是想办法通过路由器拨号。我也不算没经验的了,对openwrt这个系统有过一定研究,以前在本科的时候也是锐捷,可以用mentohust替代拨号,很简单。于是我在这里重复这样的过程,发现一直认证失败,按照网上提示的各种方法,都无法解决。
经过研究,我发现在Windows下,这里就只能用官方提供了锐捷4.90版本,从其他地方下载的更高级或者更低级的锐捷,都无法通过验证。估计就是因为这个机制,导致了mentohust难以通过验证。而且网上流行的mentohust都是基于V2协议的,但4.90是基于V4的。后来我又去下载了V4版本的进行交叉编译,测试发现还不成功。几近绝望的时候,我发现了mentohust-proxy,一个mentohust的改进版,让我找到了希望。(怎么找到它?我是直接到github搜索了,因为实在没辙了~~)
原理很简单,如果直接通过mentohust无法完成认证,那么就通过代理模式,由电脑来完成认证,而mentohust只需要负责发送心跳包维持联网就行。这是个很折中的方案,但应该说是一个很通用的方案,因为它的成功与否,基本就取决于自己电脑的锐捷客户端而已。看到这个方案,我就知道有戏了,于是赶紧补习了一下交叉编译的知识,最后成功编译好了,并且在路由上成功地完成了认证。
基于双向LSTM和迁移学习的seq2seq核心实体识别
By 苏剑林 | 2016-09-06 | 160200位读者 | 引用暑假期间做了一下百度和西安交大联合举办的核心实体识别竞赛,最终的结果还不错,遂记录一下。模型的效果不是最好的,但是胜在“端到端”,迁移性强,估计对大家会有一定的参考价值。
比赛的主题是“核心实体识别”,其实有两个任务:核心识别 + 实体识别。这两个任务虽然有关联,但在传统自然语言处理程序中,一般是将它们分开处理的,而这次需要将两个任务联合在一起。如果只看“核心识别”,那就是传统的关键词抽取任务了,不同的是,传统的纯粹基于统计的思路(如TF-IDF抽取)是行不通的,因为单句中的核心实体可能就只出现一次,这时候统计估计是不可靠的,最好能够从语义的角度来理解。我一开始就是从“核心识别”入手,使用的方法类似QA系统:
1、将句子分词,然后用Word2Vec训练词向量;
2、用卷积神经网络(在这种抽取式问题上,CNN效果往往比RNN要好)卷积一下,得到一个与词向量维度一样的输出;
3、损失函数就是输出向量跟训练样本的核心词向量的cos值。
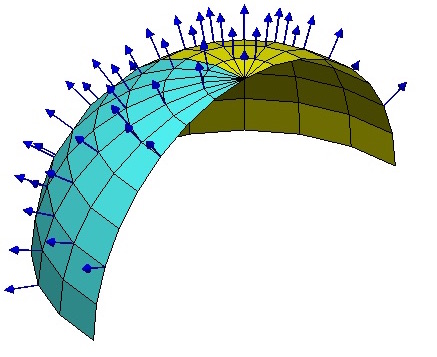
【理解黎曼几何】4. 联络和协变导数
By 苏剑林 | 2016-10-16 | 80217位读者 | 引用向量与联络
当我们在我们的位置建立起自己的坐标系后,我们就可以做很多测量,测量的结果可能是一个标量,比如温度、质量,这些量不管你用什么坐标系,它都是一样的。当然,有时候我们会测量向量,比如速度、加速度、力等,这些量都是客观实体,但因为测量结果是用坐标的分量表示的,所以如果换一个坐标,它的分量就完全不一样了。
假如所有的位置都使用同样的坐标,那自然就没有什么争议了,然而我们前面已经反复强调,不同位置的人可能出于各种原因,使用了不同的坐标系,因此,当我们写出一个向量$A^{\mu}$时,严格来讲应该还要注明是在$\boldsymbol{x}$位置测量的:$A^{\mu}(\boldsymbol{x})$,只有不引起歧义的情况下,我们才能省略它。
到这里,我们已经能够进行一些计算,比如$A^{\mu}$是在$\boldsymbol{x}$处测量的,而$\boldsymbol{x}$处的模长计算公式为$ds^2 = g_{\mu\nu} dx^{\mu} dx^{\nu}$,因此,$A^{\mu}$的模长为$\sqrt{g_{\mu\nu} A^{\mu}A^{\nu}}$,它是一个客观实体。








最近评论