Seq2Seq中Exposure Bias现象的浅析与对策
By 苏剑林 | 2020-03-09 | 94121位读者 | 引用前些天笔者写了《CRF用过了,不妨再了解下更快的MEMM?》,里边提到了MEMM的局部归一化和CRF的全局归一化的优劣。同时,笔者联想到了Seq2Seq模型,因为Seq2Seq模型的典型训练方案Teacher Forcing就是一个局部归一化模型,所以它也存在着局部归一化所带来的毛病——也就是我们经常说的“Exposure Bias”。带着这个想法,笔者继续思考了一翻,将最后的思考结果记录在此文。
本文算是一篇进阶文章,适合对Seq2Seq模型已经有一定的了解、希望进一步提升模型的理解或表现的读者。关于Seq2Seq的入门文章,可以阅读旧作《玩转Keras之seq2seq自动生成标题》和《从语言模型到Seq2Seq:Transformer如戏,全靠Mask》。
本文的内容大致为:
1、Exposure Bias的成因分析及例子;
2、简单可行的缓解Exposure Bias问题的策略。
AdaFactor优化器浅析(附开源实现)
By 苏剑林 | 2020-03-23 | 82690位读者 | 引用自从GPT、BERT等预训练模型流行起来后,其中一个明显的趋势是模型越做越大,因为更大的模型配合更充分的预训练通常能更有效地刷榜。不过,理想可以无限远,现实通常很局促,有时候模型太大了,大到哪怕你拥有了大显存的GPU甚至TPU,依然会感到很绝望。比如GPT2最大的版本有15亿参数,最大版本的T5模型参数量甚至去到了110亿,这等规模的模型,哪怕在TPU集群上也没法跑到多大的batch size。
这时候通常要往优化过程着手,比如使用混合精度训练(tensorflow下还可以使用一种叫做bfloat16的新型浮点格式),即省显存又加速训练;又或者使用更省显存的优化器,比如RMSProp就比Adam更省显存。本文则介绍AdaFactor,一个由Google提出来的新型优化器,首发论文为《Adafactor: Adaptive Learning Rates with Sublinear Memory Cost》。AdaFactor具有自适应学习率的特性,但比RMSProp还要省显存,并且还针对性地解决了Adam的一些缺陷。
Adam
首先我们来回顾一下常用的Adam优化器的更新过程。设$t$为迭代步数,$\alpha_t$为当前学习率,$L(\theta)$是损失函数,$\theta$是待优化参数,$\epsilon$则是防止溢出的小正数,那么Adam的更新过程为
AdaX优化器浅析(附开源实现)
By 苏剑林 | 2020-05-11 | 32983位读者 | 引用这篇文章简单介绍一个叫做AdaX的优化器,来自《AdaX: Adaptive Gradient Descent with Exponential Long Term Memory》。介绍这个优化器的原因是它再次印证了之前在《AdaFactor优化器浅析(附开源实现)》一文中提到的一个结论,两篇文章可以对比着阅读。
Adam & AdaX
AdaX的更新格式是
\begin{equation}\left\{\begin{aligned}&g_t = \nabla_{\theta} L(\theta_t)\\
&m_t = \beta_1 m_{t-1} + \left(1 - \beta_1\right) g_t\\
&v_t = (1 + \beta_2) v_{t-1} + \beta_2 g_t^2\\
&\hat{v}_t = v_t\left/\left(\left(1 + \beta_2\right)^t - 1\right)\right.\\
&\theta_t = \theta_{t-1} - \alpha_t m_t\left/\sqrt{\hat{v}_t + \epsilon}\right.
\end{aligned}\right.\end{equation}
其中$\beta_2$的默认值是$0.0001$。对了,顺便附上自己的Keras实现:https://github.com/bojone/adax
动手做个DialoGPT:基于LM的生成式多轮对话模型
By 苏剑林 | 2020-09-07 | 99646位读者 | 引用从采样看优化:可导优化与不可导优化的统一视角
By 苏剑林 | 2020-06-23 | 54589位读者 | 引用不少读者都应该知道,损失函数与评测指标的不一致性是机器学习的典型现象之一,比如分类问题中损失函数用交叉熵,评测指标则是准确率或者F1,又比如文本生成中损失函数是teacher-forcing形式的交叉熵,评测指标则是BLEU、ROUGE等。理想情况下,当然是评测什么指标,我们就去优化这个指标,然而评测指标通常都是不可导的,而我们多数都是使用基于梯度的优化器,这就要求最小化的目标必须是可导的,这是不一致性的来源。
前些天在arxiv刷到了一篇名为《MLE-guided parameter search for task loss minimization in neural sequence modeling》的论文,顾名思义,它是研究如何直接优化文本生成的评测指标的。经过阅读,笔者发现这篇论文很有价值,事实上它提供了一种优化评测指标的新思路,适用范围并不局限于文本生成中。不仅如此,它甚至还包含了一种理解可导优化与不可导优化的统一视角。
采样视角
首先,我们可以通过采样的视角来重新看待优化问题:设模型当前参数为$\theta$,优化目标为$l(\theta)$,我们希望决定下一步的更新量$\Delta\theta$,为此,我们先构建分布
\begin{equation}p(\Delta\theta|\theta)=\frac{e^{-[l(\theta + \Delta\theta) - l(\theta)]/\alpha}}{Z(\theta)},\quad Z(\theta) = \int e^{-[l(\theta + \Delta\theta) - l(\theta)]/\alpha} d(\Delta\theta)\end{equation}
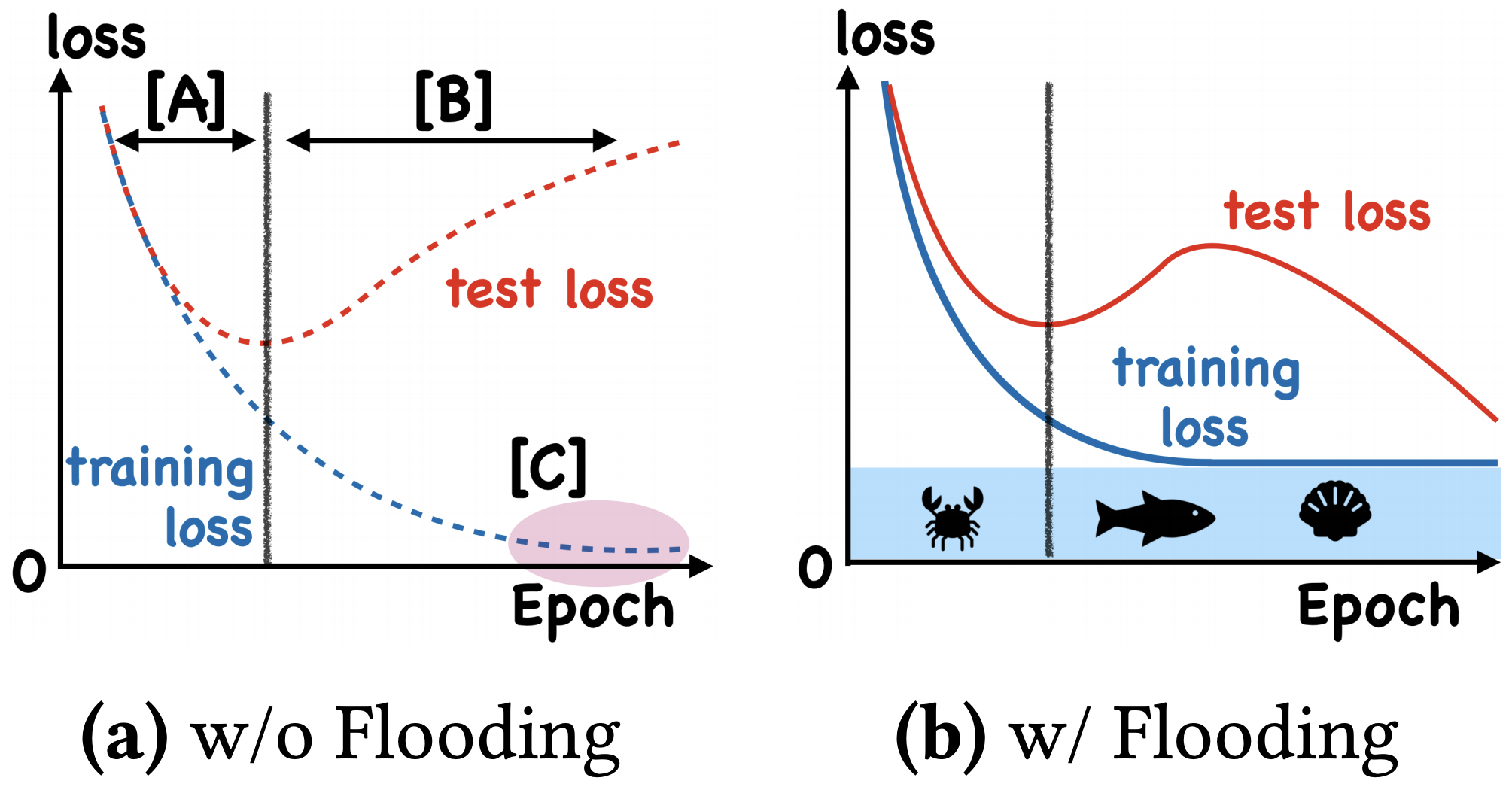
我们真的需要把训练集的损失降低到零吗?
By 苏剑林 | 2020-07-31 | 65565位读者 | 引用在训练模型的时候,我们需要损失函数一直训练到0吗?显然不用。一般来说,我们是用训练集来训练模型,但希望的是验证集的损失越小越好,而正常来说训练集的损失降低到一定值后,验证集的损失就会开始上升,因此没必要把训练集的损失降低到0。
既然如此,在已经达到了某个阈值之后,我们可不可以做点别的事情来提升模型性能呢?ICML 2020的论文《Do We Need Zero Training Loss After Achieving Zero Training Error?》回答了这个问题。不过论文的回答也仅局限在“是什么”这个层面上,并没很好地描述“为什么”,另外看了知乎上kid丶大佬的解读,也没找到自己想要的答案。因此自己分析了一下,记录在此。
L2正则没有想象那么好?可能是“权重尺度偏移”惹的祸
By 苏剑林 | 2020-08-14 | 35067位读者 | 引用L2正则是机器学习常用的一种防止过拟合的方法(应该也是一道经常遇到的面试题)。简单来说,它就是希望权重的模长尽可能小一点,从而能抵御的扰动多一点,最终提高模型的泛化性能。但是读者可能也会发现,L2正则的表现通常没有理论上说的那么好,很多时候加了可能还有负作用。最近的一篇文章《Improve Generalization and Robustness of Neural Networks via Weight Scale Shifting Invariant Regularizations》从“权重尺度偏移”这个角度分析了L2正则的弊端,并提出了新的WEISSI正则项。整个分析过程颇有意思,在这里与大家分享一下。
相关内容
这一节中我们先简单回顾一下L2正则,然后介绍它与权重衰减的联系以及与之相关的AdamW优化器。
L2正则的理解
为什么要添加L2正则?这个问题可能有多个答案。有从Ridge回归角度回答的,有从贝叶斯推断角度回答的,这里给出从扰动敏感性的角度的理解。
再谈类别不平衡问题:调节权重与魔改Loss的对比联系
By 苏剑林 | 2020-08-31 | 75534位读者 | 引用类别不平衡问题,也称为长尾分布问题,在本博客里已经有好几次相关讨论了,比如《从loss的硬截断、软化到focal loss》、《将“Softmax+交叉熵”推广到多标签分类问题》、《通过互信息思想来缓解类别不平衡问题》。对于缓解类别不平衡,比较基本的方法就是调节样本权重,看起来“高端”一点的方法则是各种魔改loss了(比如Focal Loss、Dice Loss、Logits Adjustment等),本文希望比较系统地理解一下它们之间的联系。
从光滑准确率到交叉熵
这里的分析主要以sigmoid的2分类为主,但多数结论可以平行推广到softmax的多分类。设$x$为输入,$y\in\{0,1\}$为目标,$p_{\theta}(x) \in [0, 1]$为模型。理想情况下,当然是要评测什么指标,我们就去优化那个指标。对于分类问题来说,最朴素的指标当然就是准确率,但准确率并没有办法提供有效的梯度,所以不能直接来训练。








最近评论