齐次多项式不等式的机器证明(差分代换)
By 苏剑林 | 2014-07-06 | 50401位读者 |在高中阶段,笔者也像很多学生一样参加过数学竞赛,而在准备数学竞赛的过程中,也做过一些竞赛题,其中当然少不了不等式题目。当时,面对各种各样的不等式证明题,我总是非常茫然,因为看到答案之后,总感觉证明的构造非常神奇,但是每当我自己独立去做时,却总想不出来。于是后来就萌生了“有没有办法可以通用地证明这些不等式?”的想法。为了实现这个目的,当时就想出了本文的技巧——通过牺牲计算的简便性来换取证明的有效性。后来,我虽然没有走上数学竞赛这条路,但这个方法还是保留了下来,近日,在和数学研发论坛的朋友们讨论不等式问题时,重新拾起了这个技巧。
此前,在本博客的文章《对称多项式不等式的“物理证明”》中,已经谈到了这个技巧,只是限制于当时的知识储备,了解并不深入。而在本文中,则进行拓展了。这个技巧在当时是我自己在证明中独立发现的,而现在在网上查找时发现,前辈们(杨路、姚勇、杨学枝等)早已研究过这个技巧,称之为“差分代换”,并且已经探究过它在机器证明中的作用。该技巧可以很一般化地用于齐次/非其次不等式的证明,限于篇幅,本文只谈齐次多项式不等式,特别地,是对称齐次多项式不等式,并且发现某些可以简化之处。
基本例子
本文“老生常谈”地使用均值不等式
$$a^3+b^3+c^3\geq 3abc,\quad \forall a,b,c \geq 0$$
作为开篇说明例子。均值不等式有很多漂亮的证明方法,比如《均值不等式的两个巧妙证明》。这里使用差分代换进行“不巧妙”的证明。差分代换的技巧是假设$a\leq b\leq c$,然后使用如下代换:
$$\begin{aligned}a&=a\\
b&=a+u\\
c&=a+u+v
\end{aligned}\quad \forall a,u,v \geq 0$$
得到
$$\begin{aligned}&a^3+b^3+c^3-3abc\\
=&a^3+(a+u)^3+(a+u+v)^3-3a(a+u)(a+u+v)\\
=&3 a u^2+3 a u v+3 a v^2+2 u^3+3 u^2 v+3 u v^2+v^3\end{aligned}$$
因为最后的等式中项的系数都是正数,显然不小于0,因此该不等式就成立了。
同样的技巧可以用于非对称的不等式,比如$f(a,b,c)\geq 0$等,要求不等式在$a=b=c$时取到等号。但是由于$a,b,c$不对称,因此要对于$a,b,c$的所有序(共6种)都要用同样的方法证明一次(枚举)。而对称的作用,就是用来减少枚举的次数,比如存在一个轮换对称(或者叫循环对称),就可以将枚举次数降低为2,如果是像本例子中的全对称,则只需要进行一次检验。因为计算的过程中需要用了大量的多项式展开,尤其是变量较多或者次数较高时,人工往往难以完成,因此,差分代换技巧更适用于机器证明,即用软件来完成其中的复杂展开部分。
差分代换技巧适用范围非常广。下面我们来看一道31届IMO不等式预选题:
$$(a^2+ab+b^2)(b^2+bc+c^2)(c^2+ca+a^2)\geq (ab+bc+ca)^3$$
本题是全对称不等式,即交换任意两个变量的位置,不等式还是原样,所以可以假设$a\leq b\leq c$,设$b=a+u,c=a+u+v$,有
$$\begin{aligned}&f(a,b,c)\\
=&(a^2+ab+b^2)(b^2+bc+c^2)(c^2+ca+a^2)-(ab+bc+ca)^3\\
=&9 a^4 u^2 + 26 a^3 u^3 + 27 a^2 u^4 + 12 a u^5 + 2 u^6 + 9 a^4 u v + \\
&39 a^3 u^2 v + 54 a^2 u^3 v + 30 a u^4 v + 6 u^5 v + 9 a^4 v^2 + \\
&33 a^3 u v^2 + 48 a^2 u^2 v^2 + 30 a u^3 v^2 + 7 u^4 v^2 + \\
&10 a^3 v^3 + 21 a^2 u v^3 + 15 a u^2 v^3 + 4 u^3 v^3 + 3 a^2 v^4 + \\
&3 a u v^4 + u^2 v^4\end{aligned}$$
很长很复杂,的确,这是我用Mathematica展开的,不期望有学生在考场上使用类似技巧。但是差分代换确实是证明的一种有效手段,可以看出,最后的展开式,全部系数都是正的,因此不等式显然成立。
笔者今天还检验了很多类似的全对称不等式,均发现能够成功地实现证明,而且让我意外的是,目前我还没有找到最后的展开式出现负系数的全对称不等式。
轮换对称不等式
本节我们来证明轮换不等式:
$$4(a+b+c)^3 \geq 27(ab^2+bc^2+ca^2+abc),\quad \forall a,b,c\geq 0$$
本题不是全对称不等式,它具有一个轮换对称性,或者叫循环对称性,即在
$$\begin{aligned}&(a,b,c)\to(b,c,a)\\
&(a,b,c)\to(c,a,b)\end{aligned}$$
下保持不变。这使得我们可以确定一个最小值,比如$a$,然后分别假设$a\leq b\leq c$或$a\leq c\leq b$进行检验。
首先,记$F(a,b,c)=4(a+b+c)^3-27(ab^2+bc^2+ca^2+abc)$,对于$a\leq b\leq c$,设$b=a+u,c=a+u+v$,有
$$\begin{aligned}&F(a,a+u,a+u+v)\\
=&9 a u^2 + 5 u^3 + 9 a u v - 6 u^2 v + 9 a v^2 - 3 u v^2 + 4 v^3\end{aligned}$$
嗯?出现负系数了?不过不难处理,我们知道,$a$可以任意大,$u,v$则可以任意接近0,而不等式等号取在$u=v=0$时,那么$a$的次数实际上代表着各项的“阶”,为了处理负号项,我们把同阶的合并:
$$\begin{aligned}&F(a,a+u,a+u+v)\\
=&9 a u^2 + 5 u^3 + 9 a u v - 6 u^2 v + 9 a v^2 - 3 u v^2 + 4 v^3\\
=&9 a (u^2+uv+v^2) + (5 u^3 - 6 u^2 v - 3 u v^2 + 4 v^3)\end{aligned}$$
只需要注意到$5 u^3 - 6 u^2 v - 3 u v^2 + 4 v^3=(u - v)^2 (5 u + 4 v)$就完成了该情况的证明了。
而$a\leq c\leq b$,设$c=a+u,b=a+u+v$,有
$$\begin{aligned}&F(a,a+u+v,a+u)\\
=&9 a u^2 + 5 u^3 + 9 a u v + 21 u^2 v + 9 a v^2 + 24 u v^2 + 4 v^3\end{aligned}$$
这是简单的全正系数的情况,证明完毕。
下面来证明一条很艰深的不等式:
$$\frac{1}{4}\left(\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{d}+\frac{d^2}{a}\right)\geq \sqrt{\frac{a^4+b^4+c^4+d^4}{4}},\forall a,b,c,d\geq 0$$
本题也是轮换对称不等式,可以把题目转化为证明
$$f(a,b,c,d)=\left[\frac{1}{4}\left(\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{d}+\frac{d^2}{a}\right)\right]^4-\frac{a^4+b^4+c^4+d^4}{4}$$
的非负性,进而转化为
的非负性。$a,b,c,d$有$6! =24$种序,而轮换对称性使得序的数目减少为6。我们设$a$是最小值,依次就$b,c,d$的六种序情况进行证明。比如对$a\leq b\leq c\leq d$时,设$b=a+u,c=a+u+v,d=a+u+v+w$,展开得到一个600多行的多项式!!但是检验发现,每一项都是正系数的,于是也就完成了证明。对剩下的情况进行检验,发现只有当$a\leq c\leq d\leq b$和$a\leq c\leq b\leq d$这两种情况,才出现如下的负项
$$3248 d^{17} u^3+ 1936 d^{17} u w^2- 1360 d^{17} u^2 w$$
和
$$- 192 d^{18} u w +224 d^{18} w^2+224 d^{18} u^2$$
而这两项的非负性是显然的。
最后
本文提供的是一种“机器证明”,使用软件来不厌其烦地完成多项式的展开,直接通过判断系数的正性或者转化为一些简单的不等式来完成证明。令人惊奇的是,如果不等式是对所有的实数(而非局限于非负实数),该技巧的能力却有所欠缺,需要进一步转化才能使用,比如证明Vasible不等式$(a^2+b^2+c^2)^2\geq 3(a^3 b+b^3 c+c^3 a)$,该不等式对于一切实数的$a,b,c$都成立,但是就算我们将其局限于非负实数,用上面的技巧,无法一次直接证明,而需要进一步转化。
最后,需要解释的是,为什么本文强调“齐次”?事实上,齐次不等式才是算具有物理意义的不等式,齐次意味着左右两端的“量纲”相等,这也是我在前文说的“物理证明”的含义。如果是非其次的,不等式一般会在特定的点取等号,而不仅仅是$a=b=c$,这样会导致难度的增加。当然,我已经提及过,差分代换的应用其实非常广,经过拓展后可以用于很多非其次不等式的证明,不过这已经不在本文的范围内了。有兴趣的读者可以先阅读相关论文或书籍,有机会我们再回到这个话题上。
参考文献
《初等不等式的证明方法》 韩京俊 编著
《不等式机器证明与自动发现》 杨路 夏壁灿 著
转载到请包括本文地址:https://spaces.ac.cn/archives/2747
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Jul. 06, 2014). 《齐次多项式不等式的机器证明(差分代换) 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/2747
@online{kexuefm-2747,
title={齐次多项式不等式的机器证明(差分代换)},
author={苏剑林},
year={2014},
month={Jul},
url={\url{https://spaces.ac.cn/archives/2747}},
}







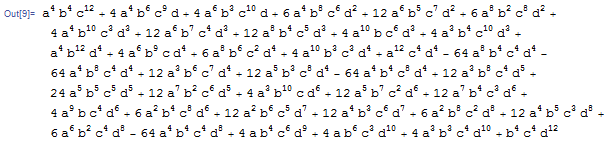



July 7th, 2014
说起自动证明,以前看到过一篇东西,说要证明(x+1)^2=x^2+2x+1,因为最高次是二次,那么只要随便代两个值成立便可直接判断这个等式成立;然后在证明三角恒等式里面,只要把里面的所有三角函数全部用万能公式换成tan(θ/2)的函数,然后再把tan(θ/2)代换成多项式自变量t,判断最高次,然后代n个值进去,如果成立,那么成立;
谢谢提供,这确实不失为一种好方法呀。当初我看到它叫做“例证法”,举例就可以证明的方法。不过,我觉得n次的至少要代入n+1个数值吧,毕竟还是有可能我们选的n个数值恰好是n个根的~
额是n+1。。大半夜的时候果然脑子不好使。。昨(jin)晚还想了几秒是不是n+1。。。
July 9th, 2014
不明觉厉啊
July 16th, 2015
怒赞!!!