科学空间|Scientific Spaces

在最优化问题中，求一个函数的最大值或最小值，最直接的方法是求导，然后比较各阶极值的大小。然而，我们所要优化的函数往往不一定可导，比如函数中含有最大值函数$\max(x,y)$的。这时候就得求助于其他思路了。有一个很巧妙的思路是，将这些不可导函数用一个可导的函数来近似它，从而我们用求极值的方法来求出它近似的最优值。本文的任务，就是探究一个简单而有用的函数，它能够作为最大值函数的近似，并且具有多阶导数。下面是笔者给出的一个推导过程。

在数学分析中，笔者已经学习过一个关于最大值函数的公式，即当$x \geq 0, y \geq 0$时，我们有
$$\max(x,y)=\frac{1}{2}\left(|x+y|+|x-y|\right)\tag{1}$$
那么，为了寻求一个最大值的函数，我们首先可以考虑寻找一个能够近似表示绝对值$|x|$的函数，这样我们就把问题从二维降低到一维了。那么，哪个函数可以使用呢？

点击阅读全文...

假设我们在听一首歌，那么听完这首歌之后，我们实际上在做这样的一个过程：耳朵接受了一段时间内的声波刺激，从而引起了大脑活动的变化。而这首歌，也就是这段时间内的声波，可以用时间$t$的函数$f(t)$描述，这个函数的区间是有限的，比如$t\in[0,T]$。接着假设另外一个场景——我们要用电脑录下我们唱的歌。这又是怎样一个过程呢？要注意电脑的信号是离散化的，而声波是连续的，因此，电脑要把歌曲记录下来，只能对信号进行采样记录。原则上来说，采集的点越多，就能够越逼真地还原我们的歌声。可是有一个问题，采集多少点才足够呢？在信息论中，一个著名的“采样定理”（又称香农采样定理，奈奎斯特采样定理）告诉我们：只需要采集有限个样本点，就能够完整地还原我们的输入信号来！

采集有限个点就能够还原一个连续的函数？这是怎么做到的？下面我们来解释这个定理。

任意给定一个函数，一般来说我们都可以将它做傅里叶变换：
$$F(\omega)=\int_{-\infty}^{+\infty} f(t)e^{i\omega t}dt\tag{1}$$
虽然我们的积分限写了正负无穷，但是由于$f(t)$是有限区间内的函数，所以上述积分区间实际上是有限的。

点击阅读全文...

问题来源

笔者经常学习的数学研发论坛曾有一帖讨论下述非线性差分方程的渐近求解：
$$a_{n+1}=a_n+\frac{1}{a_n^2},\, a_1=1$$
原帖子在这里，从这帖子中我获益良多，学习到了很多新技巧。主要思路是通过将两边立方，然后设$x_n=a_n^3$，变为等价的递推问题：
$$x_{n+1}=x_n+3+\frac{3}{x_n}+\frac{1}{x_n^2},\,x_1=1$$
然后可以通过巧妙的技巧得到渐近展开式：
$$x_n = 3n+\ln n+a+\frac{\frac{1}{3}(\ln n+a)-\frac{5}{18}}{n}+\dots$$
具体过程就不提了，读者可以自行到上述帖子学习。

然而，这种形式的解虽然精妙，但存在一些笔者不是很满意的地方：

1、解是渐近的级数，这就意味着实际上收敛半径为0；
2、是$n^{-k}$形式的解，对于较小的$n$难以计算，这都使得高精度计算变得比较困难；
3、当然，题目本来的目的是渐近计算，但是渐近分析似乎又没有必要展开那么多项；
4、里边带有了一个本来就比较难计算的极限值$a$；
5、求解过程似乎稍欠直观。

当然，上面这些缺点，有些是鸡蛋里挑骨头的。不过，也正是这些缺点，促使我寻找更好的形式的解，最终导致了这篇文章。

点击阅读全文...

魏尔斯特拉斯定理

将狄拉克函数理解为函数的极限，可以衍生出很丰富的内容，而且这些内容离严格的证明并不遥远。比如，定义
$$\delta_n(x)=\left\{\begin{aligned}&\frac{(1-x^2)^n}{I_n},x\in[-1,1]\\
&0,\text{其它情形}\end{aligned}\right.$$
其中$I_n = \int_{-1}^1 (1-x^2)^n dx$，于是不难证明
$$\delta(x)=\lim_{n\to\infty}\delta_n(x)$$
这样，对于$[a,b]$上的连续函数$f(x)$，我们就得到
$$f(x)=\int_{-1}^1 f(y)\delta(x-y)dy = \lim_{n\to\infty}\int_{-1}^1 f(y)\delta_n(x-y) dy$$
这里$-1 < a < b < 1$，并且我们已经“不严谨”地交换了积分号和极限号，但这不是特别重要。重要的是它的结果：可以看到
$$P_n(x)=\int_{-1}^1 f(y)\delta_n(x-y) dy$$
是$x$的一个$2n$次多项式，因此上式表明$f(x)$是一个$2n$次的多项式的极限！这就引出了著名的“魏尔斯特拉斯定理”：

闭区间上的连续函数都可以用多项式一致地逼近。

点击阅读全文...

Keras是一个搭积木式的深度学习框架，用它可以很方便且直观地搭建一些常见的深度学习模型。在tensorflow出来之前，Keras就已经几乎是当时最火的深度学习框架，以theano为后端，而如今Keras已经同时支持四种后端：theano、tensorflow、cntk、mxnet（前三种官方支持，mxnet还没整合到官方中），由此可见Keras的魅力。

Keras是很方便，然而这种方便不是没有代价的，最为人诟病之一的缺点就是灵活性较低，难以搭建一些复杂的模型。的确，Keras确实不是很适合搭建复杂的模型，但并非没有可能，而是搭建太复杂的模型所用的代码量，跟直接用tensorflow写也差不了多少。但不管怎么说，Keras其友好、方便的特性（比如那可爱的训练进度条），使得我们总有使用它的场景。这样，如何更灵活地定制Keras模型，就成为一个值得研究的课题了。这篇文章我们来关心自定义loss。

输入-输出设计

Keras的模型是函数式的，即有输入，也有输出，而loss即为预测值与真实值的某种误差函数。Keras本身也自带了很多loss函数，如mse、交叉熵等，直接调用即可。而要自定义loss，最自然的方法就是仿照Keras自带的loss进行改写。

点击阅读全文...

激活函数是神经网络中非线性的来源，因为如果去掉这些函数，那么整个网络就只剩下线性运算，线性运算的复合还是线性运算的，最终的效果只相当于单层的线性模型。

那么，常见的激活函数有哪些呢？或者说，激活函数的选择有哪些指导原则呢？是不是任意的非线性函数都可以做激活函数呢？

这里探究的激活函数是中间层的激活函数，而不是输出的激活函数。最后的输出一般会有特定的激活函数，不能随意改变，比如二分类一般用sigmoid函数激活，多分类一般用softmax激活，等等；相比之下，中间层的激活函数选择余地更大一些。

浮点误差都行！

理论上来说，只要是非线性函数，都有做激活函数的可能性，一个很有说服力的例子是，最近OpenAI成功地利用了浮点误差来做激活函数，其中的细节，请阅读OpenAI的博客：
https://blog.openai.com/nonlinear-computation-in-linear-networks/

或者阅读机器之心的介绍：
https://mp.weixin.qq.com/s/PBRzS4Ol_Zst35XKrEpxdw

点击阅读全文...

一般来说，神经网络处理的东西都是连续的浮点数，标准的输出也是连续型的数字。但实际问题中，我们很多时候都需要一个离散的结果，比如分类问题中我们希望输出正确的类别，“类别”是离散的，“类别的概率”才是连续的；又比如我们很多任务的评测指标实际上都是离散的，比如分类问题的正确率和F1、机器翻译中的BLEU，等等。

还是以分类问题为例，常见的评测指标是正确率，而常见的损失函数是交叉熵。交叉熵的降低与正确率的提升确实会有一定的关联，但它们不是绝对的单调相关关系。换句话说，交叉熵下降了，正确率不一定上升。显然，如果能用正确率的相反数做损失函数，那是最理想的，但正确率是不可导的（涉及到$\text{argmax}$等操作），所以没法直接用。

这时候一般有两种解决方案；一是动用强化学习，将正确率设为奖励函数，这是“用牛刀杀鸡”的方案；另外一种是试图给正确率找一个光滑可导的近似公式。本文就来探讨一下常见的不可导函数的光滑近似，有时候我们称之为“光滑化”，有时候我们也称之为“软化”。

max

后面谈到的大部分内容，基础点就是$\max$操作的光滑近似，我们有：
\begin{equation}\max(x_1,x_2,\dots,x_n) = \lim_{K\to +\infty}\frac{1}{K}\log\left(\sum_{i=1}^n e^{K x_i}\right)\end{equation}

点击阅读全文...

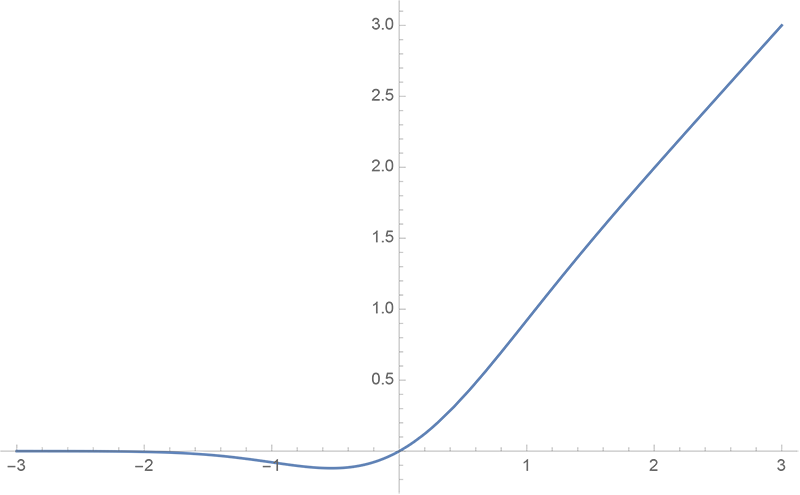
GELU，全称为Gaussian Error Linear Unit，也算是RELU的变种，是一个非初等函数形式的激活函数。它由论文《Gaussian Error Linear Units (GELUs)》提出，后来被用到了GPT中，再后来被用在了BERT中，再再后来的不少预训练语言模型也跟着用到了它。随着BERT等预训练语言模型的兴起，GELU也跟着水涨船高，莫名其妙地就成了热门的激活函数了。

gelu函数图像

在GELU的原始论文中，作者不仅提出了GELU的精确形式，还给出了两个初等函数的近似形式，本文来讨论它们是怎么得到的。

点击阅读全文...