GELU的两个初等函数近似是怎么来的

GELU，全称为Gaussian Error Linear Unit，也算是RELU的变种，是一个非初等函数形式的激活函数。它由论文《Gaussian Error Linear Units (GELUs)》提出，后来被用到了GPT中，再后来被用在了BERT中，再再后来的不少预训练语言模型也跟着用到了它。随着BERT等预训练语言模型的兴起，GELU也跟着水涨船高，莫名其妙地就成了热门的激活函数了。

在GELU的原始论文中，作者不仅提出了GELU的精确形式，还给出了两个初等函数的近似形式，本文来讨论它们是怎么得到的。

GELU函数 #

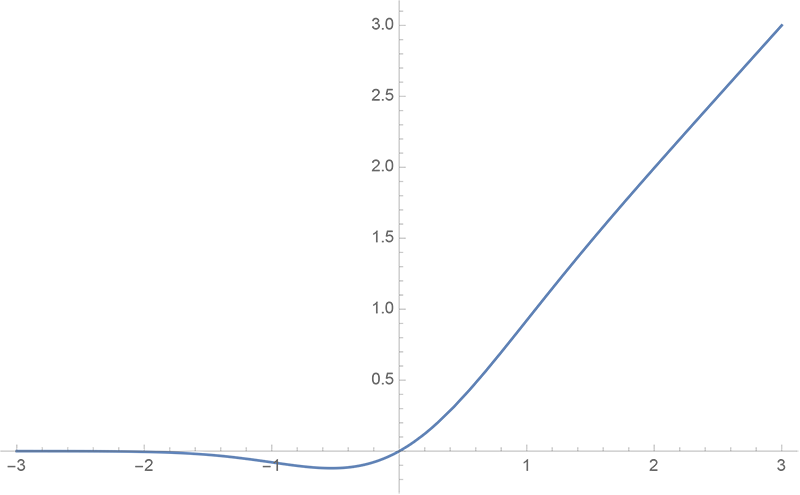
GELU函数的形式为

$$\begin{equation}\text{GELU}(x)=x \Phi(x)\end{equation}$$
其中$\Phi(x)$是标准正态分布的累积分布函数，即
$$\begin{equation}\Phi(x)=\int_{-\infty}^x \frac{e^{-t^2/2}}{\sqrt{2\pi}}dt=\frac{1}{2}\left[1 + \text{erf}\left(\frac{x}{\sqrt{2}}\right)\right]\end{equation}$$
这里$\text{erf}(x)=\frac{2}{\sqrt{\pi}}\int_0^x e^{-t^2}dt$。然后原论文还提了两个近似：
$$\begin{equation}x\Phi(x)\approx x\sigma(1.702 x)\label{eq:x-sigma}\end{equation}$$
以及
$$\begin{equation}x\Phi(x)\approx \frac{1}{2} x \left[1 + \tanh\left(\sqrt{\frac{2}{\pi}}\left(x + 0.044715 x^3\right)\right)\right]\label{eq:x-phi}\end{equation}$$
现在仍然有不少Transformer架构模型的实现都是用近似$\eqref{eq:x-phi}$作为GELU函数的实现。不过很多框架已经有精确的$\text{erf}$计算函数了，所以初等函数近似形式的价值可能不会很大，因此大家就当是一道数学分析练习题吧～

用啥近似 #

显然，要找GELU的近似形式，就相当于找$\Phi(x)$近似，这也等价于找$\text{erf}\left(\frac{x}{\sqrt{2}}\right)$的近似。

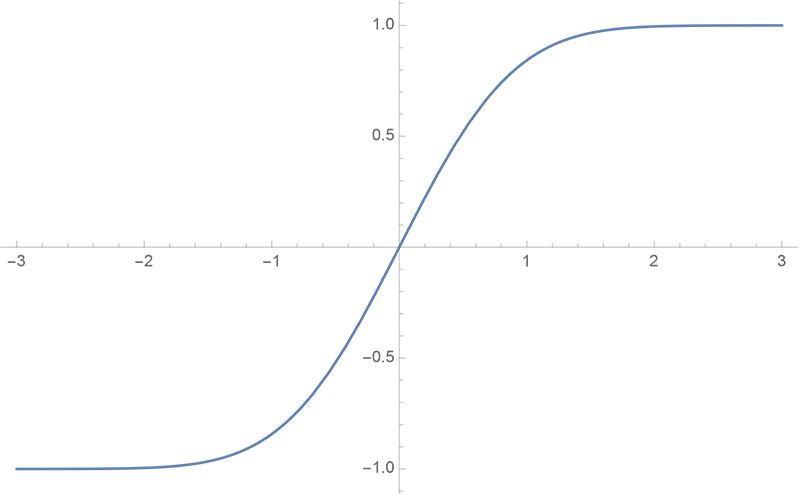
首先，我们要解决第一个问题：用什么函数来近似。从$\text{erf}(x)$图像我们可以看出它的特点：

1、它是一个奇函数，即$\text{erf}(x)=-\text{erf}(-x)$；

2、它单调递增，并且$\lim\limits_{x\to -\infty}\text{erf}(x)=-1, \lim\limits_{x\to +\infty}\text{erf}(x)=1$。

奇函数我们有很多，比如$x^{2n+1},\sin x, \tan x, \tanh x$等，并且奇函数的叠加、复合函数依然是奇函数，比如$\sin\left(x + x^3\right)$；又是奇函数，又单调递增且有界的，我们最容易想到的可能是$\tanh x$，事实上，$\tanh x$确实跟$\text{erf}(x)$很相似。

因此，我们可以从$\tanh x$出发，构造一些可能的拟合形式，比如

$$\begin{equation}\left\{\begin{aligned} &\tanh\left(a x + b x^3 + c x^5\right)\\ &a\tanh x + b \tanh^3 x + c \tanh^5 x\\ &a\tanh bx + c \tanh dx + e \tanh fx\\ &\vdots \end{aligned}\right.\end{equation}$$

怎样近似 #

有了待拟合的形式之外，下面要考虑的就是怎么拟合、以什么标准拟合的问题了，说白了，就是想个办法求出各项系数来。一般来说，有两种思路：局部拟合和全局拟合。

局部拟合 #

局部拟合基于泰勒展开，比如考虑近似形式$\tanh\left(a x + b x^3\right)$，我们在$x=0$处展开，得到

$$\begin{equation}\text{erf}\left(\frac{x}{\sqrt{2}}\right) - \tanh\left(a x + b x^3\right)=\left(\sqrt{\frac{2}{\pi }}-a\right) x + \left(\frac{a^3}{3}-b-\frac{1}{3 \sqrt{2 \pi }}\right)x^3 + \dots\end{equation}$$
让前两项为0，刚好得到两个方程，求解得到
$$\begin{equation}a=\sqrt{\frac{2}{\pi}},\quad b=\frac{4-\pi }{3 \sqrt{2} \pi ^{3/2}}\end{equation}$$
代入$x\Phi(x)$，并换成数值形式，那么就是
$$\begin{equation}x\Phi(x)\approx \frac{1}{2} x\left[1 + \tanh\left(\sqrt{\frac{2}{\pi}}\left(x + 0.0455399 x^3\right)\right)\right]\label{eq:x-phi-local}\end{equation}$$

全局拟合 #

式$\eqref{eq:x-phi-local}$已经跟式$\eqref{eq:x-phi}$很接近了，但是第二个系数还是差了点。这是因为$\eqref{eq:x-phi-local}$纯粹是局部近似的结果，顾名思义，局部近似在局部会很精确，比如上面的推导是基于$x=0$处的泰勒展开，因此在$x=0$附近会比较精确，但是离0远一点时误差就会更大。因此，我们还需要考虑全局误差。

比较容易想到的全局误差是积分形式的，比如用$g(x,\theta)$去逼近$f(x)$时，我们去算

$$\begin{equation}\min_{\theta} \int [f(x)-g(x,\theta)]^2 dx \quad\text{或}\quad \min_{\theta} \int |f(x)-g(x,\theta)| dx \end{equation}$$
但是，每个$x$处的误差重要性可能不一样，因此为了不失一般性，还要乘以一个权重$\lambda(x)$，即
$$\begin{equation}\min_{\theta} \int \lambda(x)[f(x)-g(x,\theta)]^2 dx \quad\text{或}\quad \min_{\theta} \int \lambda(x)|f(x)-g(x,\theta)| dx \end{equation}$$
不同的$\lambda(x)$会导致不同的解，哪个$\lambda(x)$最适合，也不容易选择。

因此，我们不去优化这种积分形式的误差，我们优化一个更直观的$\min-\max$形式的误差：

$$\begin{equation}\min_{\theta} \max_x |f(x)-g(x,\theta)|\end{equation}$$
这个式子很好理解，就是“找一个适当的$\theta$，使得最大的$|f(x)-g(x,\theta)|$都尽可能小”，这样的目标符合我们的直观理解，并且不涉及到权重的选取。

混合拟合 #

基于这个思想，我们固定$a=\sqrt{\frac{2}{\pi}}$，然后去重新求解$\tanh\left(a x + b x^3\right)$。固定这个$a$是因为它是一阶局部近似，我们希望保留一定的局部近似，同时希望$b$能尽可能帮我们减少全局误差，从而实现局部近似与全局近似的混合。所以，现在我们要求解

$$\begin{equation}\min_{b} \max_x \left|\text{erf}\left(\frac{x}{\sqrt{2}}\right)-\tanh\left(a x + b x^3\right)\right|\end{equation}$$
用scipy可以轻松完成求解：

import numpy as np
from scipy.special import erf
from scipy.optimize import minimize

def f(x, b):
    a = np.sqrt(2 / np.pi)
    return np.abs(erf(x / np.sqrt(2)) - np.tanh(a * x + b * x**3))

def g(b):
    return np.max([f(x, b) for x in np.arange(0, 4, 0.001)])

options = {'xtol': 1e-10, 'ftol': 1e-10, 'maxiter': 100000}
result = minimize(g, 0, method='Powell', options=options)
print(result.x)

最后得到$b=0.035677337314877385$，对应的形式就是：

$$\begin{equation}x\Phi(x)\approx \frac{1}{2} x\left[1 + \tanh\left(\sqrt{\frac{2}{\pi}}\left(x + 0.04471491123850965 x^3\right)\right)\right]\label{eq:x-phi-global}\end{equation}$$
最后几位有效数字可能有误差，但前面部分已经跟式$\eqref{eq:x-phi}$完美契合了～补充说明下，式$\eqref{eq:x-phi}$提出自论文《Approximations to the Cumulative Normal Function and its Inverse for Use on a Pocket Calculator》，已经是40多年前的结果了。

至于第一个近似，则来自论文《A logistic approximation to the cumulative normal distribution》，它是直接用$\sigma(\lambda x)$全局逼近$\Phi(x)$的结果，即

$$\begin{equation}\min_{\lambda}\max_{x}\left|\Phi(x) - \sigma(\lambda x)\right|\end{equation}$$
解得$\lambda=1.7017449256323682$，即
$$\begin{equation}\Phi(x)\approx \sigma(1.7017449256323682 x)\end{equation}$$
这跟式$\eqref{eq:x-sigma}$同样很吻合。

文章小结 #

本文带大家一起做了道数学分析题——介绍了GELU激活函数，并试图探索了它的两个近似形式的来源，成功了水出了这篇博文～

转载到请包括本文地址：https://spaces.ac.cn/archives/7309

更详细的转载事宜请参考：《科学空间FAQ》