科学空间|Scientific Spaces

如果说前面关于这个系列的内容还不能使得读者您感到痛快，那么接下来要讲述的最速降线和悬链线问题也许能够满足你的需要。不过在进入对最速降线问题的理论探讨之前，我们先来讲述一个发生在17世纪的激动人心的数学竞赛的故事。我相信，每一个热爱数学和物理的朋友，都将会为其所振奋，为其所感动。里边渗透的，不仅仅是一次学术的竞争，更是一代又一代的人对真理的追求与探路的不懈精神。

（以下内容来源于网络，科学空间整理）

意大利科学家伽利略在1630年提出一个分析学的基本问题── “一个质点在重力作用下，从一个给定点A到不在它垂直下方的另一点B，如果不计摩擦力，问沿着什么曲线滑下所需时间最短。”这算是这个著名问题的起源了（为什么别人没有想起这个问题呢？所以说大科学家的素质就是思考、创新，要有思想，人没有思想，就和行尸走肉没有什么区别）。可惜的是伽利略说这曲线是圆，但这却是一个错误的答案。

Brachistochrone

点击阅读全文...

$$e\approx\Big(1+3^{-2^{85}}\Big)^{9^{4^{6\times 7}}}$$

这个e的近似表达很漂亮，它恰好用到了1到9这9个数字。而且漂亮的不仅仅是这一点，大家猜猜看它的有效数字是多少位？10 位？100 位？1000 位？10000 位？

点击阅读全文...

级数是数学的一门很具有实用性的分支，而级数求和则是级数研究中的核心内容之一。很多问题都可以表示成一个级数的和或积，也就是$\sum_{i=1}^n f(i)$或者是$\prod_{i=1}^n f(i)$类型的运算。其中，$\ln(\prod_{i=1}^n f(i))=\sum_{i=1}^n \ln(f(i))=k$，因此$\prod_{i=1}^n f(i)=e^k$，也就是说，级数求积也可以变为级数求和来计算，换言之我们可以把精力放到级数求和上去。

为了解决一般的级数求和问题，我们考虑以下方程的解：
$$f(x+\epsilon)-f(x)=g(x)\tag{1}$$其中g(x)是已知的以x为变量的函数式，$\epsilon $是常数，初始条件是$f(k)=b$，要求f(x)的表达式。

点击阅读全文...

（阅读本文最好有一定的线性代数基础，至少对线性代数里边的基本概念有所了解。）

这学期已经接近尾声了，我们的《解析几何》已经讲到化简二次曲线了。可是，对于没有线性代数的其他同学们，直接用转轴和移轴这个计算公式来变换，那计算量会让我们很崩溃的；虽然那个“不变量”方法计算上有些简单，却总让人感到很诡异，总觉得不知从何而来，而且又要记一堆公式。事实上，如果有线性代数的基础，这些东西变得相当好理解的。我追求用统一的方法求解同一种问题，即用统一的方式处理所有的二次型，当然也希望计算量简单一点。

一般的模型

一般的二次型可以写成
$$x^T A x + 2 b^T x + c=0$$

其中$x,b$都是n维列向量（各元素为$x_i$和$b_i$），A是n阶方阵（各元素为$a_{ij}$），c是常数。在这里，我们只讨论n=2和n=3的情况。化简二次型的过程，可以归结为A矩阵的简化。

点击阅读全文...

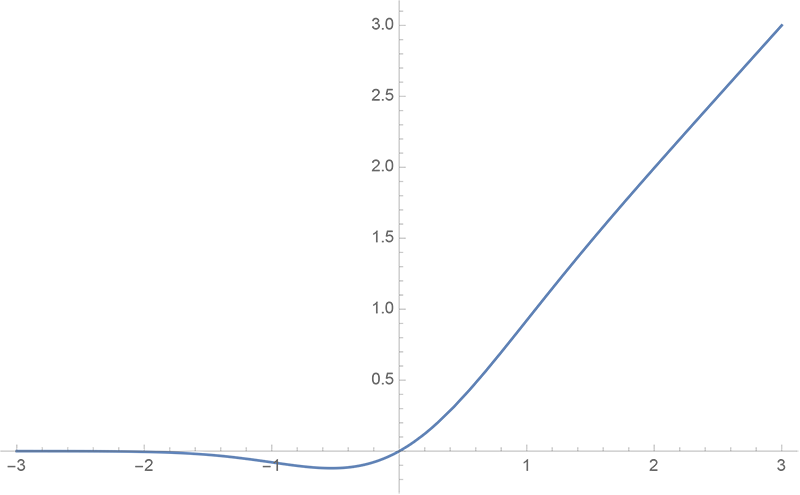
GELU，全称为Gaussian Error Linear Unit，也算是RELU的变种，是一个非初等函数形式的激活函数。它由论文《Gaussian Error Linear Units (GELUs)》提出，后来被用到了GPT中，再后来被用在了BERT中，再再后来的不少预训练语言模型也跟着用到了它。随着BERT等预训练语言模型的兴起，GELU也跟着水涨船高，莫名其妙地就成了热门的激活函数了。

gelu函数图像

在GELU的原始论文中，作者不仅提出了GELU的精确形式，还给出了两个初等函数的近似形式，本文来讨论它们是怎么得到的。

点击阅读全文...

在NLP中，我们经常要去比较两个句子的相似度，其标准方法是想办法将句子编码为固定大小的向量，然后用某种几何距离（欧氏距离、$\cos$距离等）作为相似度。这种方案相对来说比较简单，而且检索起来比较快速，一定程度上能满足工程需求。

此外，还可以直接比较两个变长序列的差异性，比如编辑距离，它通过动态规划找出两个字符串之间的最优映射，然后算不匹配程度；现在我们还有Word2Vec、BERT等工具，可以将文本序列转换为对应的向量序列，所以也可以直接比较这两个向量序列的差异，而不是先将向量序列弄成单个向量。

后一种方案速度相对慢一点，但可以比较得更精细一些，并且理论比较优雅，所以也有一定的应用场景。本文就来简单介绍一下属于后者的两个相似度指标，分别简称为WMD、WRD。

Earth Mover's Distance

本文要介绍的两个指标都是以Wasserstein距离为基础，这里会先对它做一个简单的介绍，相关内容也可以阅读笔者旧作《从Wasserstein距离、对偶理论到WGAN》。Wasserstein距离也被形象地称之为“推土机距离”（Earth Mover's Distance，EMD），因为它可以用一个“推土”的例子来通俗地表达它的含义。

点击阅读全文...

今天给大家介绍一篇1962年的论文《Computer Multiplication and Division Using Binary Logarithms》，作者是John N. Mitchell，他在里边提出了一个相当有意思的算法：在二进制下，可以完全通过加法来近似完成两个数的相乘，最大误差不超过1/9。整个算法相当巧妙，更有意思的是它还有着非常简洁的编程实现，让人拍案叫绝。然而，笔者发现网上居然找不到介绍这个算法的网页，所以在此介绍一番。

你以为这只是过时的玩意？那你就错了，前不久才有人利用它发了一篇NeurIPS 2020呢！所以，确定不来了解一下吗？

点击阅读全文...

一月份的时候，笔者写了《你可能不需要BERT-flow：一个线性变换媲美BERT-flow》，指出无监督语义相似度的SOTA模型BERT-flow其实可以通过一个简单的线性变换（白化操作，BERT-whitening）达到。随后，我们进一步完善了实验结果，写成了论文《Whitening Sentence Representations for Better Semantics and Faster Retrieval》。这篇博客将对这篇论文的内容做一个基本的梳理，并在5个中文语义相似度任务上进行了补充评测，包含了600多个实验结果。

Github链接：https://github.com/bojone/BERT-whitening

方法概要

BERT-whitening的思路很简单，就是在得到每个句子的句向量$\{x_i\}_{i=1}^N$后，对这些矩阵进行一个白化（也就是PCA），使得每个维度的均值为0、协方差矩阵为单位阵，然后保留$k$个主成分，流程如下图：

BERT-whitening的基本流程

点击阅读全文...