8
Jul
一道比较函数大小的题目
By 苏剑林 | 2011-07-08 | 21477位读者 | 引用
18
Jul
记2011北京大学天文夏令营
By 苏剑林 | 2011-07-18 | 28961位读者 | 引用
19
Jul
一道整数边三角形题目
By 苏剑林 | 2011-07-19 | 21660位读者 | 引用昨天在研究一个最优化问题时，遇到了一个这样的积分：
$$\int \frac{1}{\cos^3 \theta} d\theta$$
然后就顺便研究了一下这种类型的函数的积分。一般来讲，这类积分可以写成$\int cos^n \theta d\theta$或$\int sin^n \theta d\theta$，其中n是一个整数。
首先我们来解决n=1的情况，我们很容易就有$\int cos\theta d\theta=sin\theta +C$或$\int sin\theta d\theta=-cos\theta +C$，这是一个基本的结果。
如果n是大于1的正整数，那么可以用递推的方法来搞定：
在农村，7月是忙碌的月份，农民们要忙着收割稻谷，收割完后要晒谷，同时还得准备“下秧”，准备新一轮的耕，BoJone家自然也不例外。不过我家田比较少（1亩左右），收割机几分钟搞定，谷也三两天就晒完了。不过在晒谷的时候，BoJone在考虑一个“收谷”问题：
晒谷时得先把成堆的谷子摊开，薄薄地平铺在平地上，等到傍晚或即将下雨时（这是最惨的情况，搞不好会淋谷）就将其收起来。问题就源于这里，一般来说我们会把谷均匀地铺成矩形，要把所有的谷都推到矩形里或外的哪一点上，才使得我们做功做小？
这个问题还可以推广开来，例如对于一地任意形状的谷子（如三角形），把它集中堆到哪个点最“轻松”？一堆固定质量的谷子，要把它平铺成什么形状，才使得收谷时最“轻松”？当然，这个问题的解不仅仅用于“收谷”，在很多规划建设中也可以应用到，例如要在一个人口大致均匀的城市中建设一个服务中心，这个服务中心应该建在哪里？这有点类似于我们之前讨论过的费马点问题 ，都是费马点只考虑了三个点的距离，而这个问题得考虑所有点的距离。
27
Jul
科学空间：2011年8月重要天象
By 苏剑林 | 2011-07-27 | 17702位读者 | 引用
30
Jul
IMO42-1，我也会做几何题
By 苏剑林 | 2011-07-30 | 28995位读者 | 引用七月再次“农忙”，农村里要插秧了，播下种苗，等待再次收获的季节^_^
我一直觉得我的数学能力偏向于分析计算而不擅长于几何，纵使遇到几何问题，也是满脑子的解析几何做法，没有纯几何的美。而这几天为了加强数学竞赛题目的能力，我一直在看IMO的题目，并且企图独立做出一些题目，但都无果。我比较感兴趣的是不等式，我感觉一道简单的式子，不用太多的文字就可以讲清楚的题目非不等式莫属，但是IMO的不等式题实在高深，我还没有能够独立做出一道来（参考答案可以看懂，只是想不到思路），或许是我在努力追求统一的方法而不肯研究那些特定的技巧的原因吧。不料今天看了一下2001年IMO的几何题目，发现我可能将它做出来，于是研究了一会，最终很幸运地做了出来。虽然不是最简单的方法，但也与大家分享一下。
IMO-42-1
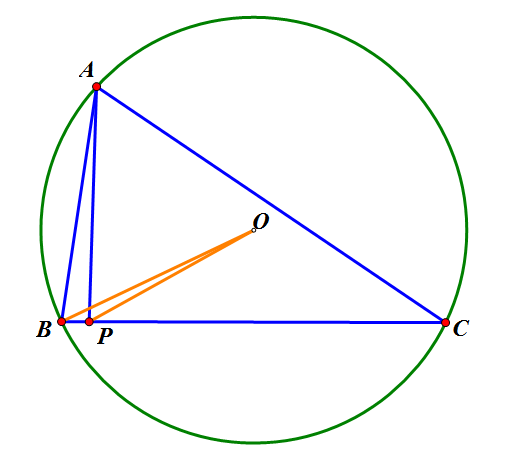
如图，O是锐角三角形ABC的外心，AP是三角形的垂线段，∠B-∠C不小于30°。证明∠BAC+∠BOP < 90°
21
Aug
有理直角三角形的面积能否为整数？
By 苏剑林 | 2011-08-21 | 38610位读者 | 引用这是一个古老而有趣的问题，但在引入这个问题之前，我们首先来看一个简单的问题：
整数边直角三角形的面积能否为一个完全平方数？
答案是不能。我们可以举一些例子来检验一下，例如边长为3,4,5的直角三角形面积为6，6不是一个平方数；再如边长为5,12,13的直角三角形面积为30，30也不是一个平方数...当然，数学的最近目的是要求严格证明，而不是简单举例，否则就只得称为不完全归纳，这样得出来的是一个猜想，而不是“定理”，就好象著名的“哥德巴赫猜想”...本文我们将试图证明这个命题。
我们稍后还会发现，这个问题和以下问题是等价的：
是否存在一个面积为1的三边长都是有理数的直角三角形？
更让人意外的是，这个问题也等价于方程$x^4+y^4=z^4$并没有整数解，换句话说，我们要证明n=4时的“费马大定理”！
最近评论