后台提示，本文是科学空间的第1000篇文章。
本想写下一篇文章的，但是看到这个提示，就先瞎写个水文纪念一下。都说人老了就喜欢各种感叹，这话还真不假。看到别人高考来个感想，博客十周年了来个感想，现在第1000篇文章了也来个感想，似乎总想找点理由感叹一下一样。那今天又能扯些啥犊子呢？
1000
首先，自恋一下。1000篇文章，如果要印刷下来，就算每篇文章印一页，那也能印个1000页了，相信不少人都没捧起过1000页的书吧（我还真读过，有文章为证：《哈哈，我的“〈圣经〉”到了》），我居然能写个1000篇，也是挺佩服自己的。当然，早期的文章有部分是转载的，不是全部都自己写的，不过还是坚持了不少原创内容，而且就算是转载的也是经过自己编辑整理的，不算纯Copy，所以也勉强能说的过去吧。
然后，庆幸一下。博客开始的主题是天文和科普，后来慢慢偏向了理论物理和数学，现在则偏向了机器学习，但不管怎样，总算很庆幸地在科学这条路坚持了下来。虽然没有像幼时设想的那样成为一名真正的自然科学家/数学家，但终究有点相关，闲时依然可以做做科学计算，勉强也对得起当初的梦想。
19
Oct
BERT可以上几年级了？Seq2Seq“硬刚”小学数学应用题
By 苏剑林 | 2020-10-19 | 66279位读者 | 引用
“鸡兔同笼”的那些年
“盈亏问题”、“年龄问题”、“植树问题”、“牛吃草问题”、“利润问题”...，小学阶段你是否曾被各种花样的数学应用题折磨过呢？没关系，现在机器学习模型也可以帮助我们去解答应用题了，来看看它可以上几年级了？
本文将给出一个求解小学数学应用题（Math Word Problem）的baseline，基于ape210k数据集训练，直接用Seq2Seq模型生成可执行的数学表达式，最终Large版本的模型能达到75%的准确率，明显高于ape210k论文所报告的结果。所谓“硬刚”，指的是没有对表达式做特别的转换，也没有通过模板处理，就直接生成跟人类做法相近的可读表达式。
27
Oct
TeaForN：让Teacher Forcing更有“远见”一些
By 苏剑林 | 2020-10-27 | 39167位读者 | 引用Teacher Forcing是Seq2Seq模型的经典训练方式，而Exposure Bias则是Teacher Forcing的经典缺陷，这对于搞文本生成的同学来说应该是耳熟能详的事实了。笔者之前也曾写过博文《Seq2Seq中Exposure Bias现象的浅析与对策》，初步地分析过Exposure Bias问题。
Teacher Forcing示意图
本文则介绍Google新提出的一种名为“TeaForN”的缓解Exposure Bias现象的方案，来自论文《TeaForN: Teacher-Forcing with N-grams》，它通过嵌套迭代的方式，让模型能提前预估到后$N$个token（而不仅仅是当前要预测的token），其处理思路上颇有可圈可点之处，值得我们学习。
（注：为了尽量跟本博客旧文章保持一致，本文的记号与原论文的记号有所不同，请大家以理解符号含义为主，不要强记符号形式。）
6
Nov
那个屠榜的T5模型，现在可以在中文上玩玩了
By 苏剑林 | 2020-11-06 | 126868位读者 | 引用不知道大家对Google去年的屠榜之作T5还有没有印象？就是那个打着“万事皆可Seq2Seq”的旗号、最大搞了110亿参数、一举刷新了GLUE、SuperGLUE等多个NLP榜单的模型，而且过去一年了，T5仍然是SuperGLUE榜单上的第一，目前还稳妥地拉开着第二名2%的差距。然而，对于中文界的朋友来说，T5可能没有什么存在感，原因很简单：没有中文版T5可用。不过这个现状要改变了，因为Google最近放出了多国语言版的T5（mT5），里边当然是包含了中文语言。虽然不是纯正的中文版，但也能凑合着用一下。
“万事皆可Seq2Seq”的T5
本文将会对T5模型做一个简单的回顾与介绍，然后再介绍一下如何在bert4keras中调用mT5模型来做中文任务。作为一个原生的Seq2Seq预训练模型，mT5在文本生成任务上的表现还是相当不错的，非常值得一试。
11
Nov
当GPT遇上中国象棋：写过文章解过题，要不再来下盘棋？
By 苏剑林 | 2020-11-11 | 52129位读者 | 引用
中国象棋
不知道读者有没有看过量子位年初的文章《最强写作AI竟然学会象棋和作曲，语言模型跨界操作引热议，在线求战》，里边提到有网友用GPT2模型训练了一个下国际象棋的模型。笔者一直在想，这么有趣的事情怎么可以没有中文版呢？对于国际象棋来说，其中文版自然就是中国象棋了，于是我一直有想着把它的结果在中国象棋上面复现一下。拖了大半年，在最近几天终于把这个事情完成了，在此跟大家分享一下。
象棋谱式
将军不离九宫内，士止相随不出官。
象飞四方营四角，马行一步一尖冲。
炮须隔子打一子，车行直路任西东。
唯卒只能行一步，过河横进退无踪。
13
Nov
也来谈谈RNN的梯度消失/爆炸问题
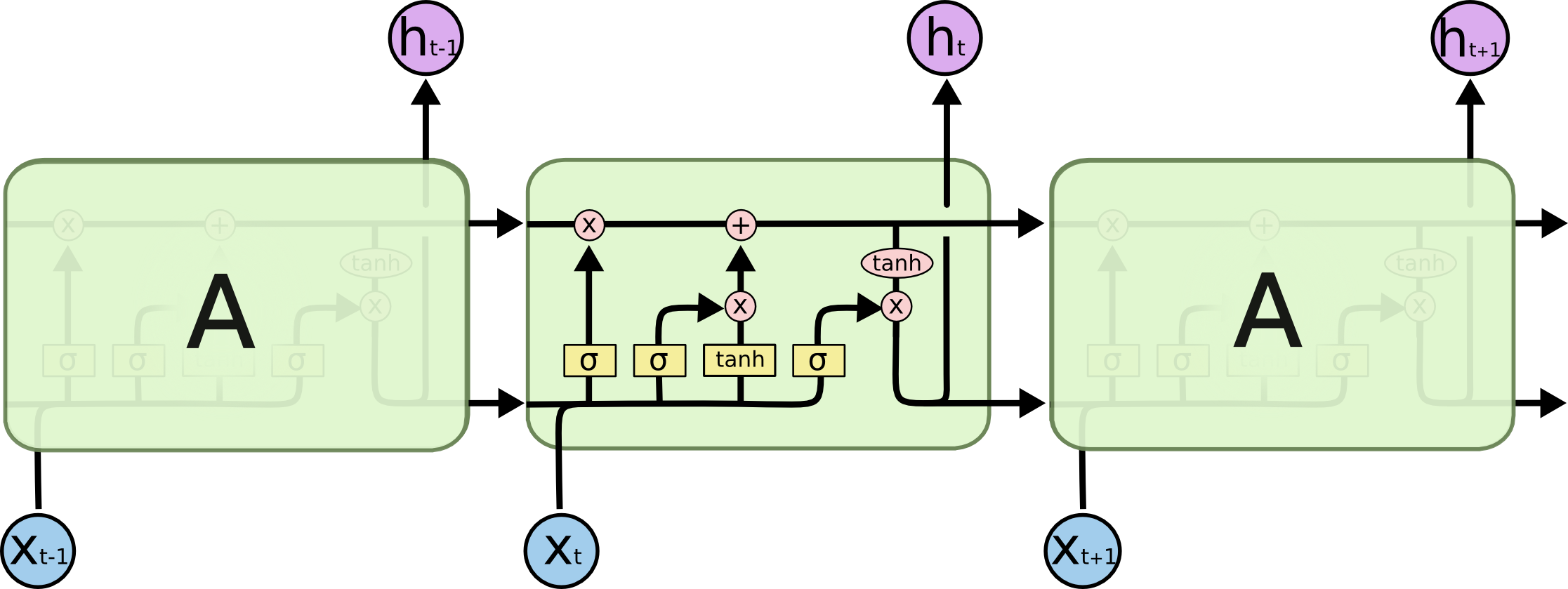
By 苏剑林 | 2020-11-13 | 87613位读者 | 引用尽管Transformer类的模型已经攻占了NLP的多数领域，但诸如LSTM、GRU之类的RNN模型依然在某些场景下有它的独特价值，所以RNN依然是值得我们好好学习的模型。而对于RNN梯度的相关分析，则是一个从优化角度思考分析模型的优秀例子，值得大家仔细琢磨理解。君不见，诸如“LSTM为什么能解决梯度消失/爆炸”等问题依然是目前流行的面试题之一...
经典的LSTM
关于此类问题，已有不少网友做出过回答，然而笔者查找了一些文章（包括知乎上的部分回答、专栏以及经典的英文博客），发现没有找到比较好的答案：有些推导记号本身就混乱不堪，有些论述过程没有突出重点，整体而言感觉不够清晰自洽。为此，笔者也尝试给出自己的理解，供大家参考。
20
Nov
跟风玩玩目前最大的中文GPT2模型（bert4keras）
By 苏剑林 | 2020-11-20 | 69693位读者 | 引用相信不少读者这几天都看到了清华大学与智源人工智能研究院一起搞的“清源计划”（相关链接《中文版GPT-3来了？智源研究院发布清源 CPM —— 以中文为核心的大规模预训练模型》），里边开源了目前最大的中文GPT2模型CPM-LM（26亿参数），据说未来还会开源200亿甚至1000亿参数的模型，要打造“中文界的GPT3”。
官方给出的CPM-LM的Few Shot效果演示图
我们知道，GPT3不需要finetune就可以实现Few Shot，而目前CPM-LM的演示例子中，Few Shot的效果也是相当不错的，让人跃跃欲试，笔者也不例外。既然要尝试，肯定要将它适配到自己的bert4keras中才顺手，于是适配工作便开始了。本以为这是一件很轻松的事情，谁知道踩坑踩了快3天才把它搞好，在此把踩坑与测试的过程稍微记录一下。
24
Nov
exp(x)在x=0处的偶次泰勒展开式总是正的
By 苏剑林 | 2020-11-24 | 34518位读者 | 引用刚看到一个有意思的结论：
对于任意实数$x$及偶数$n$，总有$\sum\limits_{k=0}^n \frac{x^k}{k!} > 0$，即$e^x$在$x=0$处的偶次泰勒展开式总是正的。
下面我们来看一下这个结论的证明，以及它在寻找softmax替代品中的应用。
证明过程
看上去这是一个很强的结果，证明会不会很复杂？其实证明非常简单，记
\begin{equation}f_n(x) = \sum\limits_{k=0}^n \frac{x^k}{k!}\end{equation}
当$n$是偶数时，我们有$\lim\limits_{x\to\pm\infty} f_n(x)=+\infty$，即整体是开口向上的，所以我们只需要证明它的最小值大于0就行了，又因为它是一个光滑连续的多项式函数，所以最小值点必然是某个极小值点。那么换个角度想，我们只需要证明它所有的极值点（不管是极大还是极小）所对应的函数值都大于0。
最近评论