exp(x)在x=0处的偶次泰勒展开式总是正的

刚看到一个有意思的结论：

对于任意实数$x$及偶数$n$，总有$\sum\limits_{k=0}^n \frac{x^k}{k!} > 0$，即$e^x$在$x=0$处的偶次泰勒展开式总是正的。

下面我们来看一下这个结论的证明，以及它在寻找softmax替代品中的应用。

证明过程 #

看上去这是一个很强的结果，证明会不会很复杂？其实证明非常简单，记
$$\begin{equation}f_n(x) = \sum\limits_{k=0}^n \frac{x^k}{k!}\end{equation}$$
当$n$是偶数时，我们有$\lim\limits_{x\to\pm\infty} f_n(x)=+\infty$，即整体是开口向上的，所以我们只需要证明它的最小值大于0就行了，又因为它是一个光滑连续的多项式函数，所以最小值点必然是某个极小值点。那么换个角度想，我们只需要证明它所有的极值点（不管是极大还是极小）所对应的函数值都大于0。

求极值点的方法自然是求导，而$f_n(x)$的一个美妙之处在于，它的导函数满足
$$\begin{equation}f_n'(x) = f_{n-1}(x)\end{equation}$$
极值点满足$f_n'(x)=0$，那也就是满足$f_{n-1}(x)=0$，此时有
$$\begin{equation}f_n(x) = f_{n-1}(x) + \frac{x^n}{n!} = \frac{x^n}{n!} \geq 0 \,\,\,(n\text{为偶数时})\end{equation}$$
因此我们就证明了$f_n(x)$的所有极值点对应的函数值都非负了，所以恒有$f_n(x)\geq 0$，并且还可以检验$x=0$并不是极值点，所以$\geq$可以改为$>$。证毕。

应用场景 #

事实上，笔者是在Arxiv的新文章《Exploring Alternatives to Softmax Function》看到这个结论的。原论文给出了一个基于数学归纳法的比较复杂的证明，上述证明则是笔者自己构思的，相对来说更加简单明了一些。

那么原论文为什么要得到这个结论呢？顾名思义，是为了探究softmax的替代品。我们知道，在机器学习中常用的将输出变为概率分布的方法是加上softmax：
$$\begin{equation}softmax(\boldsymbol{x})_i = \frac{e^{x_i}}{\sum\limits_{k=1}^n e^{x_k}}\end{equation}$$
而由于$n$是偶数是$f_n(x) > 0$，并且$f_n(x)$在一定范围内还是$e^x$的近似，所以将$e^x$换成$f_n(x)$也可以作为合理的归一化函数：
$$\begin{equation}taylor\text{-}softmax(\boldsymbol{x}, n)_i = \frac{f_n(x_i)}{\sum\limits_{k=1}^n f_n(x_k)}\end{equation}$$
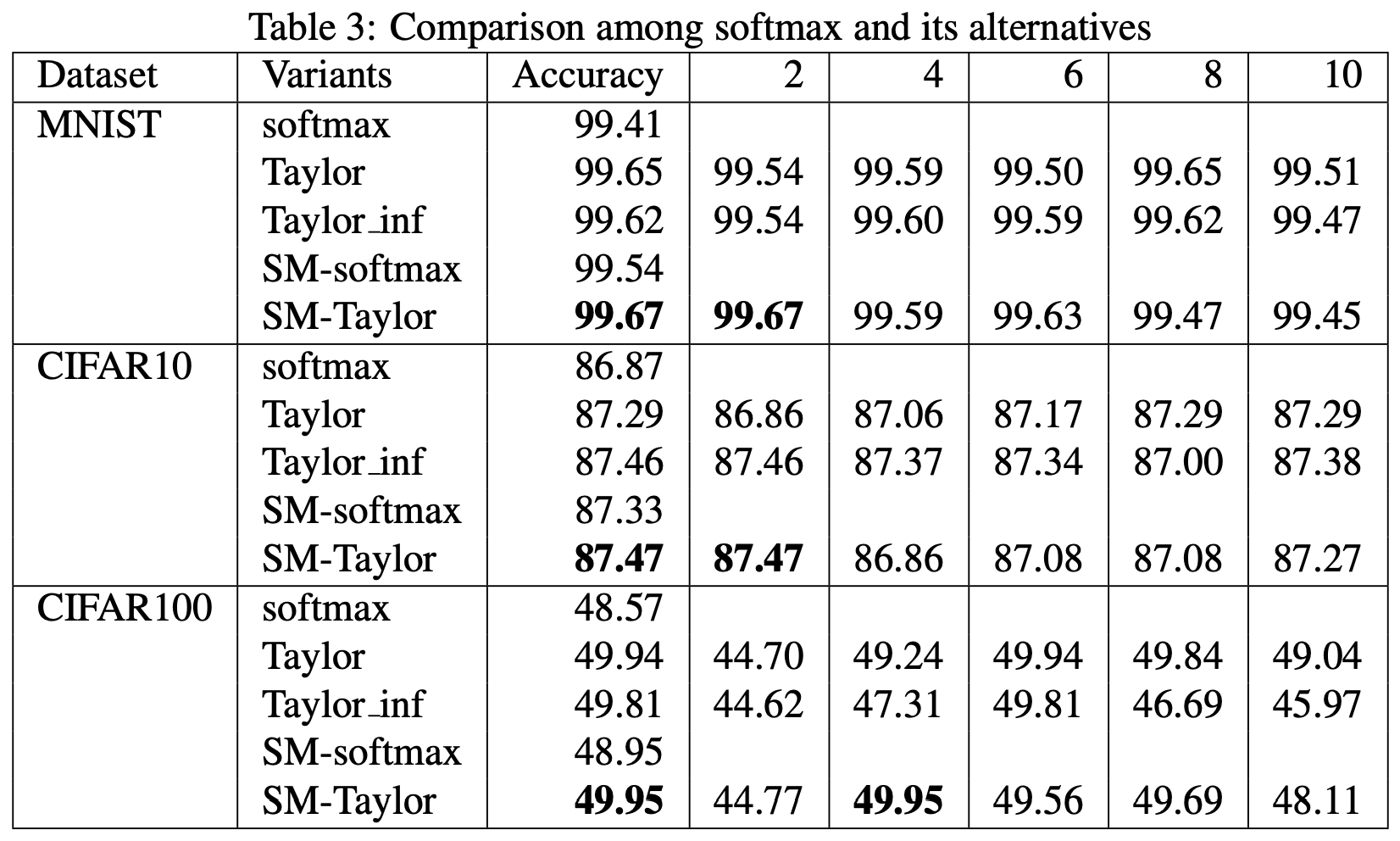
原论文做了几个实验，表明$taylor\text{-}softmax$比常规的softmax有一定的提升：

稍加评述 #

然而，在笔者看来，这个实验结果很难有什么说服力，毕竟所用的baseline效果太低了（都2020年了，你好歹跑个ResNet吧？）。此外，原论文也没有提供关于这个替代品的一些直观理解，纯粹是做了简单的实验然后说它work了，实在是过于粗糙。

不过，尽管原论文有诸多不足之处，笔者认为其提出的$taylor\text{-}softmax$倒是真的有可能是有效的。从softmax到$taylor\text{-}softmax$的过程，实际上是将激活函数从指数函数换成了多项式函数，这两者有什么区别呢？我们知道$|x|$比较大的时候，$e^x$会增加/衰减得很快，这直接导致了softmax经常给出的置信度过高的现象（概率值非0即1），而相对来说，多项式函数的增长没有那么猛，不容易出现置信度过高问题，从而没那么容易过拟合。

类似的改动也出现在经典的降维方法t-SNE中，t-SNE的前身是SNE，SNE就是构造了类似softmax的指数形式的概率分布，然后被发现有“Crowding问题”（参考《最小熵原理（四）：“物以类聚”之从图书馆到词向量》），最后t-SNE将指数换成二次函数就好很多了，感觉$taylor\text{-}softmax$跟t-SNE的思想有一定的相通之处。

保持单调 #

事实上，还可以证明$f_n(x)$全局只有一个极小值点，所以它的图像都是呈“U”字型的，如下图：

某些有强迫症的读者可能会纠结$f_n(x)$的非单调性问题，觉得$f_n(x)$不是一个单调函数可能会隐藏某些问题。事实上，当前没有什么明确的证据表明转换为概率分布的变换必须是单调的。当然，如果你依然担心，那其实也可以截断一下。刚才说了$f_n(x)$只有一个极小值点$x_n^*$，大于极小值点的部分就是单调递增的，小于极小值点的部分直接让它等于极小值点就好了，即定义
$$\begin{equation}\tilde{f}_{n}(x)=\left\{\begin{aligned}&f_n(x),\quad x > x_n^*\\ &f_n(x_n^*),\quad x\leq x_n^*\end{aligned}\right.\end{equation}$$
然后用$\tilde{f}_{n}(x)$代替$f_{n}(x)$完成归一化就行。对于固定的$n$，$x_n^*$和$f_n(x_n^*)$都可以事先用数值方法算出来：
$$\begin{array}{c|cc} \hline n & x_n^* & f(x_n^*) \\ \hline 2 & -1 & 0.5 \\ 4 & -1.59607 & 0.270395 \\ 6 & -2.18061 & 0.149325 \\ 8 & -2.759 & 0.0832715 \\ 10 & -3.33355 & 0.0466991 \\ \hline \end{array}$$

文章小结 #

文本的主要目的是介绍“$e^x$的偶次泰勒展开式总是正的”这个颇有意思的结论，并且顺带介绍了它在寻找softmax替代品中的应用。

转载到请包括本文地址：https://spaces.ac.cn/archives/7919

更详细的转载事宜请参考：《科学空间FAQ》