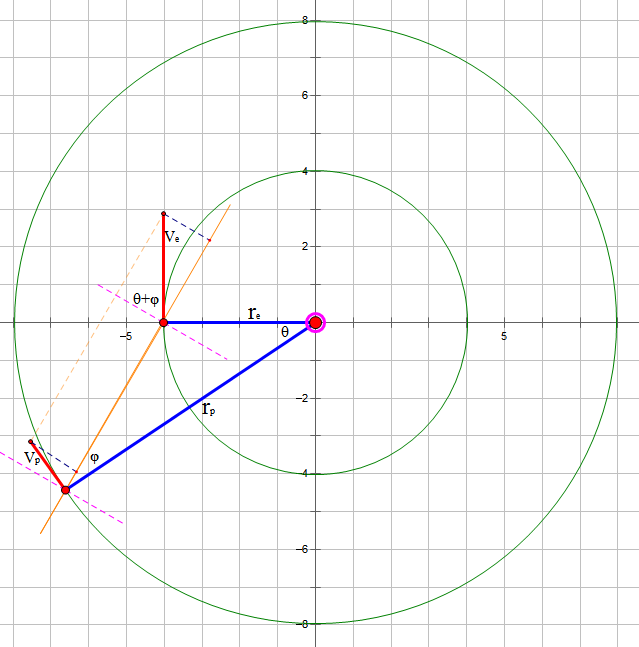
关于行星留周期的几何讨论
By 苏剑林 | 2010-10-02 | 16789位读者 | 引用《向量》系列——5.平面向量微分方程与复数
By 苏剑林 | 2010-10-03 | 20363位读者 | 引用哈勃定律——宇宙各向同性的体现
By 苏剑林 | 2010-10-04 | 22146位读者 | 引用1929年哈勃(Edwin Hubble)对河外星系的视向速度与距离的关系进行了研究。当时只有46个河外星系的视向速度可以利用,而其中仅有24个有推算出的距离,哈勃得出了视向速度与距离之间大致的线性正比关系。
不少宇宙学的书籍中都提到了标题,那么,为什么哈勃定律是宇宙各向同性的体现?或者说为什么宇宙各向同性就必然导致哈勃定律?
首先我们得需要了解一下宇宙学原理,它告诉我们宇宙在大尺度范围是均匀的、各向同性的。基于这个原理,我们会得到一些很奇怪的东西,如宇宙中的每一点都是宇宙的中心。另外,我们还可以得到:宇宙的(整体)运动情况在每一个方向都应该取相同的形式。
欣赏一张图片——I Heart Math
By 苏剑林 | 2010-10-07 | 32498位读者 | 引用以自然数幂为系数的幂级数
By 苏剑林 | 2010-10-16 | 31160位读者 | 引用$\sum_{i=0}^{\infty} a_i x^i=a_0+a_1 x+a_2 x^2+a_3 x^3+...$
最近为了数学竞赛,我研究了有关数列和排列组合的相关问题。由于我讨厌为某个问题而设计专门的技巧,所以我偏爱通用的方法,哪怕过程相对麻烦。因此,我对数学归纳法(递推法)和生成函数法情有独钟。前者只需要列出问题的递归关系,而不用具体分析,最终把问题转移到解函数方程上来。后者则巧妙地把数列${a_n}$与幂级数$\sum_{i=0}^{\infty} a_i x^i$一一对应,巧妙地通过代数运算或微积分运算等得到结果。这里我们不用考虑该级数的敛散性,只需要知道它对应着哪一个“母函数”(母函数展开泰勒级数后得到了级数$\sum_{i=0}^{\infty} a_i x^i$)。显然,这两种方法的最终,都是把问题归结为代数问题。
也许不少同好已经在一些书籍上看到过这样的论述:
各向同性的薄球壳,其内部任意一点所受到来自球壳的引力为0。
这是一个很神奇的事情,因为这意味着这是一个均匀引力场,虽然我们在很多问题上都假设了引力场均匀,但是我们却很难知道如何构造一个真正的均匀引力场(而构造一个真正的均匀力场都分析某些问题是很有用的,例如推导一些比例系数),现在眼前就摆着一个均匀引力场了。并且利用它我们就可以计算均匀实心球内部一点所受到的引力(等于它与一个球体的引力)。而关于它的证明,当然也可以利用微积分的知识,可是我们在这里介绍一个初等的方法,相信它会使我们更加感受到物理的神奇和有趣。









最近评论