球壳内部的均匀力场
By 苏剑林 | 2010-10-16 | 70707位读者 |也许不少同好已经在一些书籍上看到过这样的论述:
各向同性的薄球壳,其内部任意一点所受到来自球壳的引力为0。
这是一个很神奇的事情,因为这意味着这是一个均匀引力场,虽然我们在很多问题上都假设了引力场均匀,但是我们却很难知道如何构造一个真正的均匀引力场(而构造一个真正的均匀力场都分析某些问题是很有用的,例如推导一些比例系数),现在眼前就摆着一个均匀引力场了。并且利用它我们就可以计算均匀实心球内部一点所受到的引力(等于它与一个球体的引力)。而关于它的证明,当然也可以利用微积分的知识,可是我们在这里介绍一个初等的方法,相信它会使我们更加感受到物理的神奇和有趣。
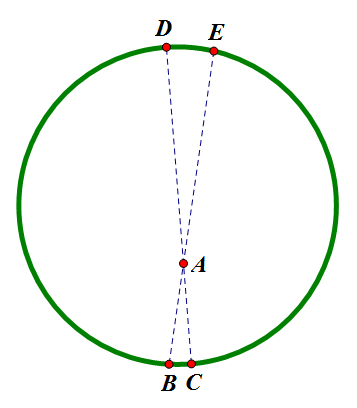
如图,我们要证明A点所受到的引力之和为0。过A点可以作两个立体角很小的对顶的圆锥,化成平面图就是图中“ΔABC和ΔADE”或“ΔAGF和ΔAHI”。以前者为例,当对顶角很小时,我们可以把DE和BC部分都其视为质点处理,并且将DE和BC看成直线(注意,它们本不是一条线,而是一个凸起的圆;看成直线后他们就是一个平面上的圆)。分别计算它们对A点的引力
$$\begin{aligned}F_{ABC}=\frac{GM_{BC}M_A}{AB^2} \\ F_{ADE}=\frac{GM_{DE}M_A}{AD^2}\end{aligned}$$
由于密度均匀
$$\frac{M_{BC}}{M_{DE}}=\frac{S_{BC}}{S_{DE}}=\frac{AB^2}{AD^2}$$
代入后,我们发现
$$F_{ABC}=F_{ADE}$$
也就是说,这两个部分的引力抵消了。一个球壳可以做无限次这种分割,而它们的引力都相互抵消,换句话说球壳的每个点对A的引力都会有另外一个点与之抵消,于是A点所受的引力为0。
由于静电力场具有和万有引力场类似的性质(和距离平方成反比),因而不难类比到,当球壳上均匀布满同种电荷时,球壳内任意点电荷所受的静电力合力为零。这时,我们不禁产生一个疑问:电荷有正负之分,要是球壳被平均分成两半,各自都均匀地分布着等量的异种电荷,那么内部的电场是怎样的呢?
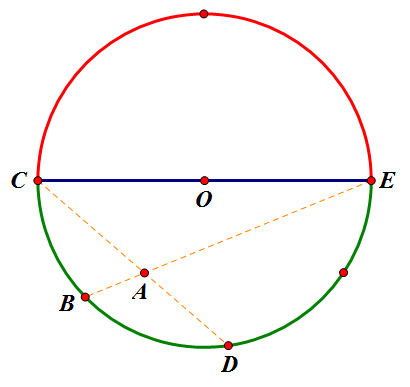
也许有朋友猜测也是匀强的,不过这样想的朋友错了。请看下图
蓝色弧和红色弧分别代表带等量的异种电荷,分析点A的受力情况,根据上面的推导方法,由于BC与DE两段弧(实际是两个凸圆)的静电力相互抵消,红色弧与BD弧的静电力相等,而且方向相同,因此可以看成:A点的受力等于半球壳CE(红色弧)对A点的合力的两倍。要是受力均匀,那就是说半球壳CE对任意点的静电力相等,这显然不符合事实。
转载到请包括本文地址:https://spaces.ac.cn/archives/988
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Oct. 16, 2010). 《球壳内部的均匀力场 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/988
@online{kexuefm-988,
title={球壳内部的均匀力场},
author={苏剑林},
year={2010},
month={Oct},
url={\url{https://spaces.ac.cn/archives/988}},
}










October 16th, 2010
难道……这就是传说中的《自然哲学之数学原理》命题70?这个结果太意外了!
那么这样继续推导下去,均匀实心球内某点所受到的引力是否正比于该点所在球面内的实心球物质质量,反比于该点与球心距离的平方?
你的推导是正确的。
本文所用的方法据说也是牛顿当时的推导方法
October 16th, 2010
要是受力均匀,那就是说半球壳CE对任意点的静电力相等,这显然不符合事实。
为什么受力均匀,半球壳CE对任意点的静电力相等?
还可以这样来证,任一点,势能相等。
请看红色部分和加粗部分。
September 6th, 2019
写得好,这其实是积分的一种简化,但由于积分的无穷性,所以计算结果还是精确附合事实,数学太美了,谢谢作者