1
Dec
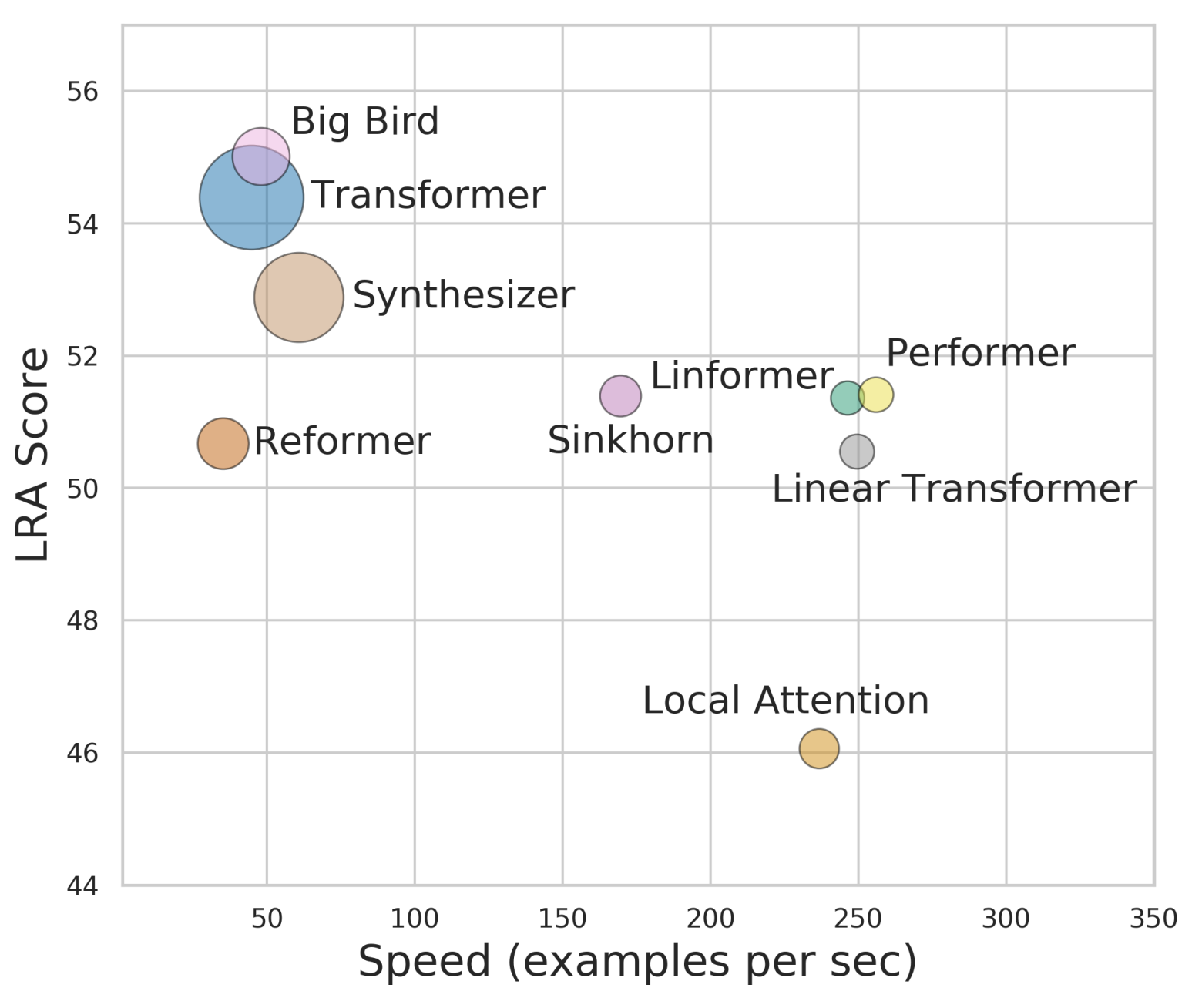
Performer：用随机投影将Attention的复杂度线性化
By 苏剑林 | 2020-12-01 | 81494位读者 | 引用Attention机制的$\mathcal{O}(n^2)$复杂度是一个老大难问题了，改变这一复杂度的思路主要有两种：一是走稀疏化的思路，比如我们以往介绍过的Sparse Attention以及Google前几个月搞出来的Big Bird，等等；二是走线性化的思路，这部分工作我们之前总结在《线性Attention的探索：Attention必须有个Softmax吗？》中，读者可以翻看一下。本文则介绍一项新的改进工作Performer，出自Google的文章《Rethinking Attention with Performers》，它的目标相当霸气：通过随机投影，在不损失精度的情况下，将Attention的复杂度线性化。
各个Transformer模型的“效果-速度-显存”图，纵轴是效果，横轴是速度，圆圈的大小代表所需要的显存。理论上来说，越靠近右上方的模型越好，圆圈越小的模型越好
说直接点，就是理想情况下我们可以不用重新训练模型，输出结果也不会有明显变化，但是复杂度降到了$\mathcal{O}(n)$！看起来真的是“天上掉馅饼”般的改进了，真的有这么美好吗？
1
Jan
SPACES：“抽取-生成”式长文本摘要（法研杯总结）
By 苏剑林 | 2021-01-01 | 233698位读者 | 引用“法研杯”算是近年来比较知名的NLP赛事之一，今年是第三届，包含四个赛道，其中有一个“司法摘要”赛道引起了我们的兴趣。经过了解，这是面向法律领域裁判文书的长文本摘要生成，这应该是国内第一个公开的长文本生成任务和数据集。过去一年多以来，我们在文本生成方面都有持续的投入和探索，所以决定选择该赛道作为检验我们研究成果的“试金石”。很幸运，我们最终以微弱的优势获得了该赛道的第一名。在此，我们对我们的比赛模型做一个总结和分享。
比赛榜单截图
在该比赛中，我们跳出了纯粹炼丹的过程，通过新型的Copy机制、Sparse Softmax等颇具通用性的新方法提升了模型的性能。整体而言，我们的模型比较简洁有效，而且可以做到端到端运行。窃以为我们的结果对工程和研究都有一定的参考价值。
14
Dec
Mitchell近似：乘法变为加法，误差不超过1/9
By 苏剑林 | 2020-12-14 | 38923位读者 | 引用今天给大家介绍一篇1962年的论文《Computer Multiplication and Division Using Binary Logarithms》，作者是John N. Mitchell，他在里边提出了一个相当有意思的算法：在二进制下，可以完全通过加法来近似完成两个数的相乘，最大误差不超过1/9。整个算法相当巧妙，更有意思的是它还有着非常简洁的编程实现，让人拍案叫绝。然而，笔者发现网上居然找不到介绍这个算法的网页，所以在此介绍一番。
你以为这只是过时的玩意？那你就错了，前不久才有人利用它发了一篇NeurIPS 2020呢！所以，确定不来了解一下吗？
7
Jan
【搜出来的文本】⋅（一）从文本生成到搜索采样
By 苏剑林 | 2021-01-07 | 61374位读者 | 引用最近，笔者入了一个新坑：基于离散优化的思想做一些文本生成任务。简单来说，就是把我们要生成文本的目标量化地写下来，构建一个分布，然后搜索这个分布的最大值点或者从这个分布中进行采样，这个过程通常不需要标签数据的训练。由于语言是离散的，因此梯度下降之类的连续函数优化方法不可用，并且由于这个分布通常没有容易采样的形式，直接采样也不可行，因此需要一些特别设计的采样算法，比如拒绝采样（Rejection Sampling）、MCMC（Markov Chain Monte Carlo）、MH采样（Metropolis-Hastings Sampling）、吉布斯采样（Gibbs Sampling），等等。
有些读者可能会觉得有些眼熟，似乎回到了让人头大的学习LDA（Latent Dirichlet Allocation）的那些年？没错，上述采样算法其实也是理解LDA模型的必备基础。本文我们就来回顾这些形形色色的采样算法，它们将会出现在后面要介绍的丰富的文本生成应用中。
26
Jan
Seq2Seq重复解码现象的理论分析尝试
By 苏剑林 | 2021-01-26 | 31803位读者 | 引用去年笔者写过博文《如何应对Seq2Seq中的“根本停不下来”问题？》，里边介绍了一篇论文中对Seq2Seq解码不停止现象的处理，并指出那篇论文只是提了一些应对该问题的策略，并没有提供原理上的理解。近日，笔者在Arixv读到了AAAI 2021的一篇名为《A Theoretical Analysis of the Repetition Problem in Text Generation》的论文，里边从理论上分析了Seq2Seq重复解码现象。从本质上来看，重复解码和解码不停止其实都是同理的，所以这篇新论文算是填补了前面那篇论文的空白。
经过学习，笔者发现该论文确实有不少可圈可点之处，值得一读。笔者对原论文中的分析过程做了一些精简、修正和推广，将结果记录成此文，供大家参考。此外，抛开问题背景不讲，读者也可以将本文当成一节矩阵分析习题课，供大家复习线性代数哈～
16
Feb
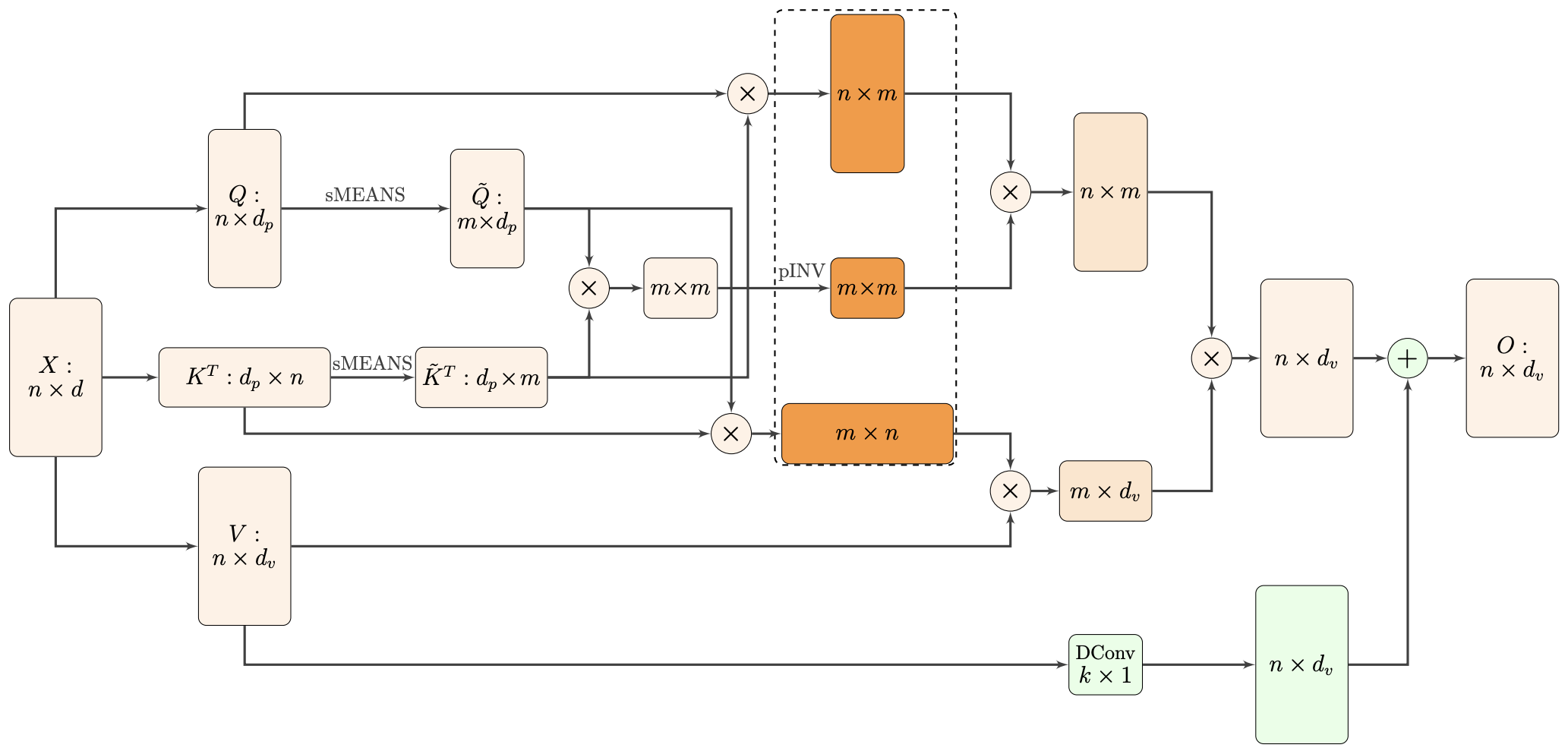
Nyströmformer：基于矩阵分解的线性化Attention方案
By 苏剑林 | 2021-02-16 | 44523位读者 | 引用标准Attention的$\mathcal{O}(n^2)$复杂度可真是让研究人员头大。前段时间我们在博文《Performer：用随机投影将Attention的复杂度线性化》中介绍了Google的Performer模型，它通过随机投影的方式将标准Attention转化为线性Attention。无独有偶，前些天Arxiv上放出了AAAI 2021的一篇论文《Nyströmformer: A Nyström-Based Algorithm for Approximating Self-Attention》，里边又提出了一种从另一个角度把标准Attention线性化的方案。
Nyströmformer结构示意图
该方案写的是Nyström-Based，顾名思义是利用了Nyström方法来近似标准Attention的。但是坦白说，在看到这篇论文之前，笔者也完全没听说过Nyström方法，而纵观整篇论文，里边也全是笔者一眼看上去感觉很茫然的矩阵分解推导，理解起来颇为困难。不过有趣的是，尽管作者的推导很复杂，但笔者发现最终的结果可以通过一个相对来说更简明的方式来理解，遂将笔者对Nyströmformer的理解整理在此，供大家参考。
8
Jul
两个多元正态分布的KL散度、巴氏距离和W距离
By 苏剑林 | 2021-07-08 | 102628位读者 | 引用正态分布是最常见的连续型概率分布之一。它是给定均值和协方差后的最大熵分布（参考《“熵”不起：从熵、最大熵原理到最大熵模型（二）》），也可以看作任意连续型分布的二阶近似，它的地位就相当于一般函数的线性近似。从这个角度来看，正态分布算得上是最简单的连续型分布了。也正因为简单，所以对于很多估计量来说，它都能写出解析解来。
本文主要来计算两个多元正态分布的几种度量，包括KL散度、巴氏距离和W距离，它们都有显式解析解。
正态分布
这里简单回顾一下正态分布的一些基础知识。注意，仅仅是回顾，这还不足以作为正态分布的入门教程。
概率密度
正态分布，也即高斯分布，是定义在$\mathbb{R}^n$上的连续型概率分布，其概率密度函数为
\begin{equation}p(\boldsymbol{x})=\frac{1}{\sqrt{(2\pi)^n \det(\boldsymbol{\Sigma})}}\exp\left\{-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{\top}\boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right\}\end{equation}
1
Jul
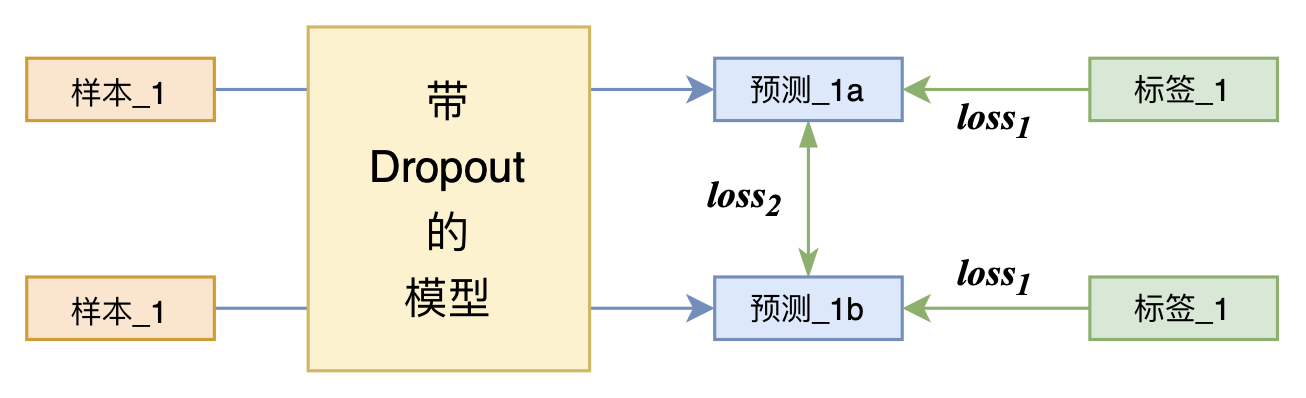
又是Dropout两次！这次它做到了有监督任务的SOTA
By 苏剑林 | 2021-07-01 | 208727位读者 | 引用关注NLP新进展的读者，想必对四月份发布的SimCSE印象颇深，它通过简单的“Dropout两次”来构造正样本进行对比学习，达到了无监督语义相似度任务的全面SOTA。无独有偶，最近的论文《R-Drop: Regularized Dropout for Neural Networks》提出了R-Drop，它将“Dropout两次”的思想用到了有监督任务中，每个实验结果几乎都取得了明显的提升。此外，笔者在自己的实验还发现，它在半监督任务上也能有不俗的表现。
R-Drop示意图
小小的“Dropout两次”，居然跑出了“五项全能”的感觉，不得不令人惊讶。本文来介绍一下R-Drop，并分享一下笔者对它背后原理的思考。
最近评论