在讨论曲线坐标系的积分时,通常都会出现行列式这个东西,作为“体积元”的因子。在广义相对论中,爱因斯坦场方程的作用量就带有度规的行列式,而在对其进行变分时,自然也就涉及到了行列式的求导问题。我参考了朗道的《场论》以及《数理物理基础--物理需用线性高等数学导引》,了解到相关结果,遂记录如下。
推导
设
\begin{equation}\boldsymbol{A}(t)=\left(a_{ij}(t)\right)_{n\times n}\end{equation}
是一个n阶矩阵,其中每个矩阵元素都是t的函数。其行列式为$|\boldsymbol{A}|$,自然地,考虑
\begin{equation}\frac{d}{dt}|\boldsymbol{A}|\end{equation}
翻到新的维度,把积分解决!
By 苏剑林 | 2014-02-25 | 47658位读者 | 引用一般来说,如果原函数容易找到的话,牛顿-莱布尼兹公式是定积分的通用方法。但是牛顿-莱布尼兹公式只适合连续函数的积分,如果积分区间含有奇点,那就不成立了。比如,我们考虑积分
$$\int_{-1}^1 \frac{1}{x^2}dx$$
当然,从严格的数学上来说,这种写法是不成立的,因为被积函数在原点没有意义。当然,从物理的角度来考虑,由于对称性,我们确信
$$\int_{-1}^1 \frac{1}{x^2}dx=2\int_{0}^1 \frac{1}{x^2}dx=\lim_{\varepsilon\to 0}2\int_{\varepsilon}^1 \frac{1}{x^2}dx$$
从而得出积分发散的结论。这种处理某种程度上是可以接受的,但是却不是让人满意的,因为它导致了分段。有什么办法可以直接处理这种情况呢?确实有的,同样引入参数,并且最终让参数为0,考虑带参数的积分
$$\int_{-1}^1 \frac{1}{x^2+\varepsilon^2}dx$$
只要参数为正,这个被积函数就在$\mathbb{R}$上处处连续了,也就是奇点消失了,这样子就可以用牛顿-莱布尼兹公式了
$$\int_{-1}^1 \frac{1}{x^2+\varepsilon^2}dx=\left.\frac{1}{\varepsilon}\arctan\left(\frac{x}{\varepsilon}\right)\right|_{-1}^{1}$$
考虑$\varepsilon\to 0$的情况,就自动得到了积分发散的结论。
三个相切圆的公切圆:补充
By 苏剑林 | 2014-01-30 | 31692位读者 | 引用在学车的时候,我堂大哥曾问我一道作圆的问题:
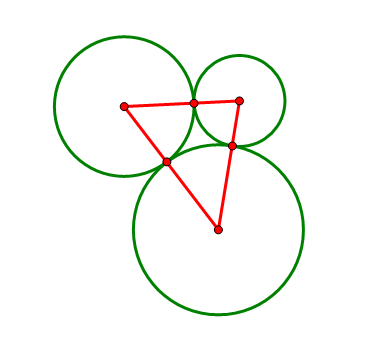
平面上给出三个两两相切的圆以及它们的圆心,求作一个圆与这三个圆都相切(尺规作图)。
如果从纯几何的途径入手,我们甚至很难判断这样的圆是否存在。但是我之前似乎已经看过类似的题目,于是很快想到一个名词:反演。反演可以将圆反演成直线(圆过反演点),也可以将圆反演成圆(圆不过反演点),而其他的相切、相交等关系保持不变。对反演后的图形进行相同的反演,就变回原来的图形。本题的难点在于圆太多,利用反演,我们可以将它变为两条直线和一个圆的问题。
假设读者已经有了反演的基本知识,如果没有,请到
http://zh.wikipedia.org/wiki/反演
阅读相关内容。
几何的数与数的几何:超复数的浅探究
By 苏剑林 | 2014-01-11 | 72257位读者 | 引用这也是我的期末论文之一...全文共17页,包括了四元数的构造方法,初等应用等。附录包括行列式与体积、三维旋转的描述等。使用LaTex进行写作(LaTex会让你爱上数学写作的)
几何的数与数的几何
――超复数的浅探究
摘要
今天,不论是数学还是物理的高维问题,都采用向量分析为基本工具,数学物理中难觅四元数的影子。然而在历史上,四元数的发展有着重要的意义。四元数(Quaternion)运算实际上是向量分析的“鼻祖”,向量点积和叉积的概念也首先出现在四元数的运算中,四元数的诞生还标记着非交换代数的开端。即使是现在,四元数还是计算机描述三维空间旋转问题最简单的工具。另外,作为复数的推广,四元数还为某些复数问题的一般化提供了思路。
本文把矩阵与几何适当地结合起来,利用矩阵行列式$\det (AB) =(\det A)(\det B)$这一性质得出了四元数以及更高维的超复数的生成规律,并讨论了它的一些性质以及它在描述旋转方面的应用。部分证明细节和不完善的思想放到了附录之中。
不确定性原理的矩阵形式
By 苏剑林 | 2014-01-05 | 57118位读者 | 引用作为量子理论的一个重要定理,不确定性原理总是伴随着物理意义出现的,但是从数学的角度来讲,把不确定性原理的数学形式抽象出来,有助于我们发现更多领域的“不确定性原理”。
本文中,我们将谈及不确定性原理的n维矩阵形式。首先需要解释给大家的是,不确定性原理其实是关于“两个厄密算符与一个单位向量之间的一条不等式”。在量子力学中,厄密算符对应着无穷维的厄密矩阵;而所谓厄密矩阵,就是一个矩阵同时取共轭和转置之后,等于它自身。但是本文讨论一个更简单的情况,那就是n维实矩阵,n维实矩阵中的厄密矩阵就是我们所说的实对称矩阵了。
设$\boldsymbol{x}$是一个$n$维单位向量,即$|\boldsymbol{x}|=1$,而$\boldsymbol{A}$和$\boldsymbol{B}$是n阶实对称矩阵。在量子力学中,$\boldsymbol{x}$就是波函数,但是在这里,它只不过是一个单位实向量;并记$\boldsymbol{I}$是$n$阶单位阵。
考虑
$$\bar{A}=\boldsymbol{x}^{T}\boldsymbol{A}\boldsymbol{x},\bar{B}=\boldsymbol{x}^{T}\boldsymbol{B}\boldsymbol{x}$$
从这些记号可以看出,这些量对应着可观测量的期望值。当然,如果不懂量子力学,可以只看上面的矩阵形式。
矩阵描述三维空间旋转
By 苏剑林 | 2013-12-28 | 119915位读者 | 引用本节简单介绍用矩阵来描述旋转。在二维平面上,复数无疑是描述旋转的最佳工具;然而推广到三维空间中,却要动用到“四元数”了。为了证明四元数的相关结论,我们需要三维旋转的矩阵描述。最一般的旋转运动为:绕某一根轴旋转$\theta$角度。这样我们就需要三个参数来描述它:确定一根轴至少需要两个参数,确定角度需要一个参数。因此,如果要用“数”来描述三维空间的伸缩和旋转的话,“三元数”显然是不够的,完成这一目的至少需要四元数。这也从另外一个角度反映了三元数的不存在性。
矩阵方法
首先我们认识到,如果旋转轴是坐标轴之一,那么旋转矩阵将是最简单的,比如向量$\boldsymbol{x}=(x_0,y_0,z_0)^{T}$绕$z$轴逆时针旋转$\theta$角后的坐标就可以描述为
$$\begin{equation}
\boldsymbol{R}_{\theta}\boldsymbol{x}\end{equation}$$








最近评论