Monarch矩阵:计算高效的稀疏型矩阵分解
By 苏剑林 | 2024-07-24 | 1731位读者 | 引用在矩阵压缩这个问题上,我们通常有两个策略可以选择,分别是低秩化和稀疏化。低秩化通过寻找矩阵的低秩近似来减少矩阵尺寸,而稀疏化则是通过减少矩阵中的非零元素来降低矩阵的复杂性。如果说SVD是奔着矩阵的低秩近似去的,那么相应地寻找矩阵稀疏近似的算法又是什么呢?
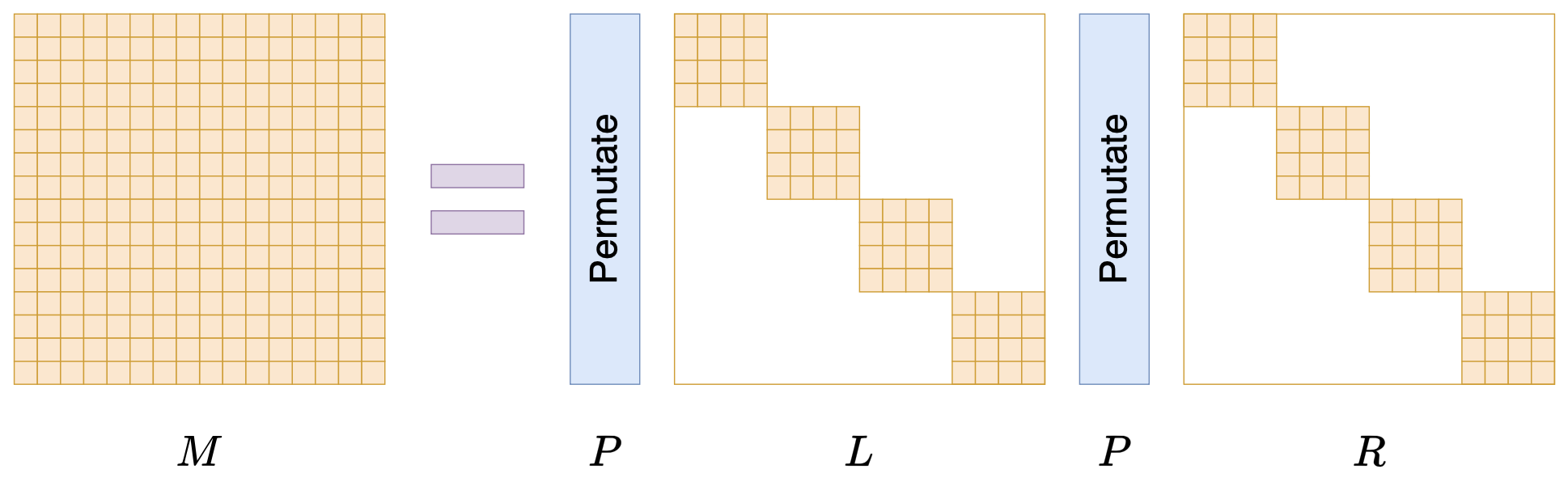
接下来我们要学习的是论文《Monarch: Expressive Structured Matrices for Efficient and Accurate Training》,它为上述问题给出了一个答案——“Monarch矩阵”,这是一簇能够分解为若干置换矩阵与稀疏矩阵乘积的矩阵,同时具备计算高效且表达能力强的特点,论文还讨论了如何求一般矩阵的Monarch近似,以及利用Monarch矩阵参数化LLM来提高LLM速度等内容。
值得指出的是,该论文的作者也正是著名的Flash Attention的作者Tri Dao,其工作几乎都在致力于改进LLM的性能,这篇Monarch也是他主页上特意展示的几篇论文之一,单从这一点看就非常值得学习一番。
对齐全量微调!这是我看过最精彩的LoRA改进(一)
By 苏剑林 | 2024-07-12 | 11138位读者 | 引用众所周知,LoRA是一种常见的参数高效的微调方法,我们在《梯度视角下的LoRA:简介、分析、猜测及推广》做过简单介绍。LoRA利用低秩分解来降低微调参数量,节省微调显存,同时训练好的权重可以合并到原始权重上,推理架构不需要作出改变,是一种训练和推理都比较友好的微调方案。此外,我们在《配置不同的学习率,LoRA还能再涨一点?》还讨论过LoRA的不对称性,指出给$A,B$设置不同的学习率能取得更好的效果,该结论被称为“LoRA+”。
为了进一步提升效果,研究人员还提出了不少其他LoRA变体,如AdaLoRA、rsLoRA、DoRA、PiSSA等,这些改动都有一定道理,但没有特别让人深刻的地方觉。然而,前两天的《LoRA-GA: Low-Rank Adaptation with Gradient Approximation》,却让笔者眼前一亮,仅扫了摘要就有种必然有效的感觉,仔细阅读后更觉得它是至今最精彩的LoRA改进。
究竟怎么个精彩法?LoRA-GA的实际含金量如何?我们一起来学习一下。
重温SSM(四):有理生成函数的新视角
By 苏剑林 | 2024-06-27 | 7404位读者 | 引用在前三篇文章中,我们较为详细地讨论了HiPPO和S4的大部分数学细节。那么,对于接下来的第四篇文章,大家预期我们会讨论什么工作呢?S5、Mamba乃至Mamba2?都不是。本系列文章主要关心SSM的数学基础,旨在了解SSM的同时也补充自己的数学能力。而在上一篇文章我们简单提过S5和Mamba,S5是S4的简化版,相比S4基本上没有引入新的数学技巧,而Mamba系列虽然表现优异,但它已经将$A$简化为对角矩阵,所用到的数学技巧就更少了,它更多的是体现了工程方面的能力。
这篇文章我们来学习一篇暂时还声名不显的新工作《State-Free Inference of State-Space Models: The Transfer Function Approach》(简称RFT),它提出了一个新方案,将SSM的训练、推理乃至参数化,都彻底转到了生成函数空间中,为SSM的理解和应用开辟了新的视角
基础回顾
首先我们简单回顾一下上一篇文章关于S4的探讨结果。S4基于如下线性RNN
\begin{equation}\begin{aligned}
x_{k+1} =&\, \bar{A} x_k + \bar{B} u_k \\
y_{k+1} =&\, \bar{C}^* x_{k+1} \\
\end{aligned}\label{eq:linear}\end{equation}
重温SSM(三):HiPPO的高效计算(S4)
By 苏剑林 | 2024-06-20 | 9472位读者 | 引用前面我们用两篇文章《重温SSM(一):线性系统和HiPPO矩阵》和《重温SSM(二):HiPPO的一些遗留问题》介绍了HiPPO的思想和推导——通过正交函数基对持续更新的函数进行实时逼近,其拟合系数的动力学正好可以表示为一个线性ODE系统,并且对于特定的基底以及逼近方式,我们可以将线性系统的关键矩阵精确地算出来。此外,我们还讨论了HiPPO的离散化和相关性质等问题,这些内容奠定了后续的SSM工作的理论基础。
接下来,我们将介绍HiPPO的后续应用篇《Efficiently Modeling Long Sequences with Structured State Spaces》(简称S4),它利用HiPPO的推导结果作为序列建模的基本工具,并从新的视角探讨了高效的计算和训练方式,最后在不少长序列建模任务上验证了它的有效性,可谓SSM乃至RNN复兴的代表作之一。
基本框架
S4使用的序列建模框架,是如下的线性ODE系统:
\begin{equation}\begin{aligned}
x'(t) =&\, A x(t) + B u(t) \\
y(t) =&\, C^* x(t) + D u(t)
\end{aligned}\end{equation}
通向概率分布之路:盘点Softmax及其替代品
By 苏剑林 | 2024-06-14 | 13211位读者 | 引用不论是在基础的分类任务中,还是如今无处不在的注意力机制中,概率分布的构建都是一个关键步骤。具体来说,就是将一个$n$维的任意向量,转换为一个$n$元的离散型概率分布。众所周知,这个问题的标准答案是Softmax,它是指数归一化的形式,相对来说比较简单直观,同时也伴有很多优良性质,从而成为大部分场景下的“标配”。
尽管如此,Softmax在某些场景下也有一些不如人意之处,比如不够稀疏、无法绝对等于零等,因此很多替代品也应运而生。在这篇文章中,我们将简单总结一下Softmax的相关性质,并盘点和对比一下它的部分替代方案。
Softmax回顾
首先引入一些通用记号:$\boldsymbol{x} = (x_1,x_2,\cdots,x_n)\in\mathbb{R}^n$是需要转为概率分布的$n$维向量,它的分量可正可负,也没有限定的上下界。$\Delta^{n-1}$定义为全体$n$元离散概率分布的集合,即
\begin{equation}\Delta^{n-1} = \left\{\boldsymbol{p}=(p_1,p_2,\cdots,p_n)\left|\, p_1,p_2,\cdots,p_n\geq 0,\sum_{i=1}^n p_i = 1\right.\right\}\end{equation}
之所以标注$n-1$而不是$n$,是因为约束$\sum\limits_{i=1}^n p_i = 1$定义了$n$维空间中的一个$n-1$维子平面,再加上$p_i\geq 0$的约束,$(p_1,p_2,\cdots,p_n)$的集合就只是该平面的一个子集,即实际维度只有$n-1$。
重温SSM(二):HiPPO的一些遗留问题
By 苏剑林 | 2024-06-05 | 12433位读者 | 引用书接上文,在上一篇文章《重温SSM(一):线性系统和HiPPO矩阵》中,我们详细讨论了HiPPO逼近框架其HiPPO矩阵的推导,其原理是通过正交函数基来动态地逼近一个实时更新的函数,其投影系数的动力学正好是一个线性系统,而如果以正交多项式为基,那么线性系统的核心矩阵我们可以解析地求解出来,该矩阵就称为HiPPO矩阵。
当然,上一篇文章侧重于HiPPO矩阵的推导,并没有对它的性质做进一步分析,此外诸如“如何离散化以应用于实际数据”、“除了多项式基外其他基是否也可以解析求解”等问题也没有详细讨论到。接下来我们将补充探讨相关问题。
离散格式
假设读者已经阅读并理解上一篇文章的内容,那么这里我们就不再进行过多的铺垫。在上一篇文章中,我们推导出了两类线性ODE系统,分别是:
\begin{align}
&\text{HiPPO-LegT:}\quad x'(t) = Ax(t) + Bu(t) \label{eq:legt-ode}\\[5pt]
&\text{HiPPO-LegS:}\quad x'(t) = \frac{A}{t}x(t) + \frac{B}{t}u(t) \label{eq:legs-ode}\end{align}
其中$A,B$是与时间$t$无关的常数矩阵,HiPPO矩阵主要指矩阵$A$。在这一节中,我们讨论这两个ODE的离散化。
重温SSM(一):线性系统和HiPPO矩阵
By 苏剑林 | 2024-05-24 | 20948位读者 | 引用前几天,笔者看了几篇介绍SSM(State Space Model)的文章,才发现原来自己从未认真了解过SSM,于是打算认真去学习一下SSM的相关内容,顺便开了这个新坑,记录一下学习所得。
SSM的概念由来已久,但这里我们特指深度学习中的SSM,一般认为其开篇之作是2021年的S4,不算太老,而SSM最新最火的变体大概是去年的Mamba。当然,当我们谈到SSM时,也可能泛指一切线性RNN模型,这样RWKV、RetNet还有此前我们在《Google新作试图“复活”RNN:RNN能否再次辉煌?》介绍过的LRU都可以归入此类。不少SSM变体致力于成为Transformer的竞争者,尽管笔者并不认为有完全替代的可能性,但SSM本身优雅的数学性质也值得学习一番。
尽管我们说SSM起源于S4,但在S4之前,SSM有一篇非常强大的奠基之作《HiPPO: Recurrent Memory with Optimal Polynomial Projections》(简称HiPPO),所以本文从HiPPO开始说起。
以蒸馏的名义:“从去噪自编码器到生成模型”重现江湖
By 苏剑林 | 2024-05-01 | 21938位读者 | 引用今天我们分享一下论文《Score identity Distillation: Exponentially Fast Distillation of Pretrained Diffusion Models for One-Step Generation》,顾名思义,这是一篇探讨如何更快更好地蒸馏扩散模型的新论文。
即便没有做过蒸馏,大家应该也能猜到蒸馏的常规步骤:随机采样大量输入,然后用扩散模型生成相应结果作为输出,用这些输入输出作为训练数据对,来监督训练一个新模型。然而,众所周知作为教师的原始扩散模型通常需要多步(比如1000步)迭代才能生成高质量输出,所以且不论中间训练细节如何,该方案的一个显著缺点是生成训练数据太费时费力。此外,蒸馏之后的学生模型通常或多或少都有效果损失。
有没有方法能一次性解决这两个缺点呢?这就是上述论文试图要解决的问题。








最近评论