科学空间|Scientific Spaces

（注：本文的相关内容已整理成论文《ZLPR: A Novel Loss for Multi-label Classification》，如需引用可以直接引用英文论文，谢谢。）

一般来说，在处理常规的多分类问题时，我们会在模型的最后用一个全连接层输出每个类的分数，然后用softmax激活并用交叉熵作为损失函数。在这篇文章里，我们尝试将“Softmax+交叉熵”方案推广到多标签分类场景，希望能得到用于多标签分类任务的、不需要特别调整类权重和阈值的loss。

类别不平衡

单标签到多标签

一般来说，多分类问题指的就是单标签分类问题，即从$n$个候选类别中选$1$个目标类别。假设各个类的得分分别为$s_1,s_2,
\dots,s_n$，目标类为$t\in\{1,2,\dots,n\}$，那么所用的loss为
\begin{equation}-\log \frac{e^{s_t}}{\sum\limits_{i=1}^n e^{s_i}}= - s_t + \log \sum\limits_{i=1}^n e^{s_i}\label{eq:log-softmax}\end{equation}
这个loss的优化方向是让目标类的得分$s_t$变为$s_1,s_2,\dots,s_t$中的最大值。关于softmax的相关内容，还可以参考《寻求一个光滑的最大值函数》、《函数光滑化杂谈：不可导函数的可导逼近》等文章。

点击阅读全文...

GELU，全称为Gaussian Error Linear Unit，也算是RELU的变种，是一个非初等函数形式的激活函数。它由论文《Gaussian Error Linear Units (GELUs)》提出，后来被用到了GPT中，再后来被用在了BERT中，再再后来的不少预训练语言模型也跟着用到了它。随着BERT等预训练语言模型的兴起，GELU也跟着水涨船高，莫名其妙地就成了热门的激活函数了。

gelu函数图像

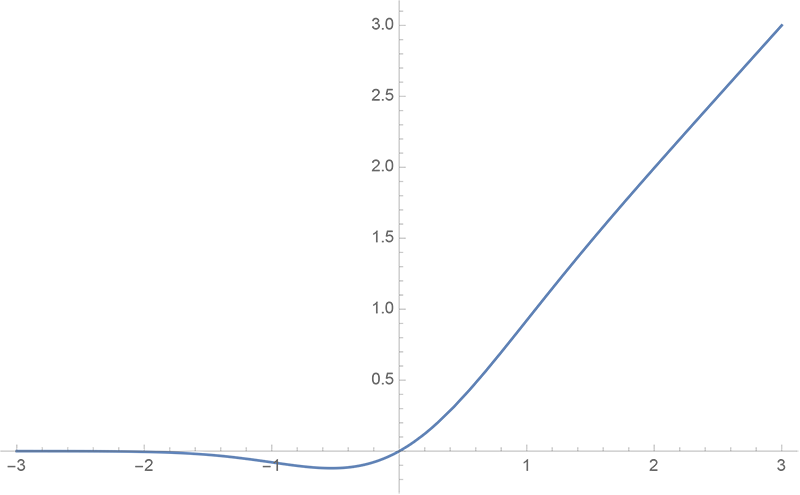
在GELU的原始论文中，作者不仅提出了GELU的精确形式，还给出了两个初等函数的近似形式，本文来讨论它们是怎么得到的。

点击阅读全文...

生成模型一直是笔者比较关注的主题，不管是NLP和CV的生成模型都是如此。这篇文章里，我们介绍一个新颖的生成模型，来自论文《Batch norm with entropic regularization turns deterministic autoencoders into generative models》，论文中称之为EAE（Entropic AutoEncoder）。它要做的事情给变分自编码器（VAE）基本一致，最终效果其实也差不多（略优），说它新颖并不是它生成效果有多好，而是思路上的新奇，颇有别致感。此外，借着这个机会，我们还将学习一种统计量的估计方法——$k$邻近方法，这是一种很有用的非参数估计方法。

自编码器vs生成模型

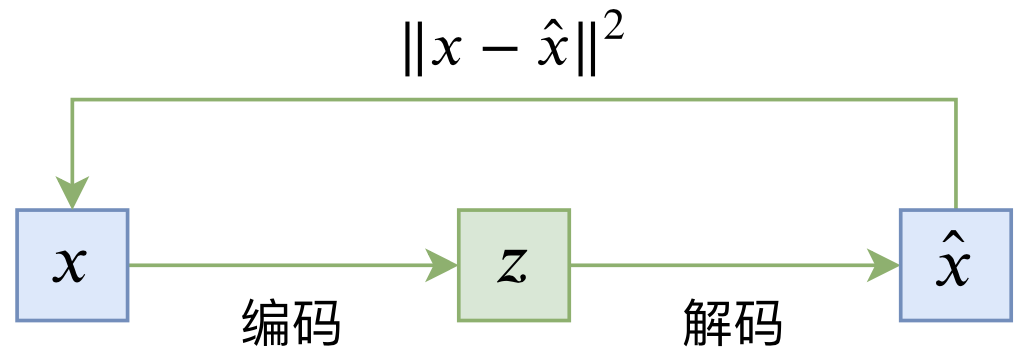
普通的自编码器是一个“编码-解码”的重构过程，如下图所示：

典型自编码器示意图

其loss一般为
\begin{equation}L_{AE} = \mathbb{E}_{x\sim \tilde{p}(x)}\left[\left\Vert x - \hat{x}\right\Vert^2\right] = \mathbb{E}_{x\sim \tilde{p}(x)}\left[\left\Vert x - D(E(x))\right\Vert^2\right]\end{equation}

点击阅读全文...

这篇文章简单介绍一个叫做AdaX的优化器，来自《AdaX: Adaptive Gradient Descent with Exponential Long Term Memory》。介绍这个优化器的原因是它再次印证了之前在《AdaFactor优化器浅析（附开源实现）》一文中提到的一个结论，两篇文章可以对比着阅读。

Adam & AdaX

AdaX的更新格式是
\begin{equation}\left\{\begin{aligned}&g_t = \nabla_{\theta} L(\theta_t)\\
&m_t = \beta_1 m_{t-1} + \left(1 - \beta_1\right) g_t\\
&v_t = (1 + \beta_2) v_{t-1} + \beta_2 g_t^2\\
&\hat{v}_t = v_t\left/\left(\left(1 + \beta_2\right)^t - 1\right)\right.\\
&\theta_t = \theta_{t-1} - \alpha_t m_t\left/\sqrt{\hat{v}_t + \epsilon}\right.
\end{aligned}\right.\end{equation}
其中$\beta_2$的默认值是$0.0001$。对了，顺便附上自己的Keras实现：https://github.com/bojone/adax

点击阅读全文...

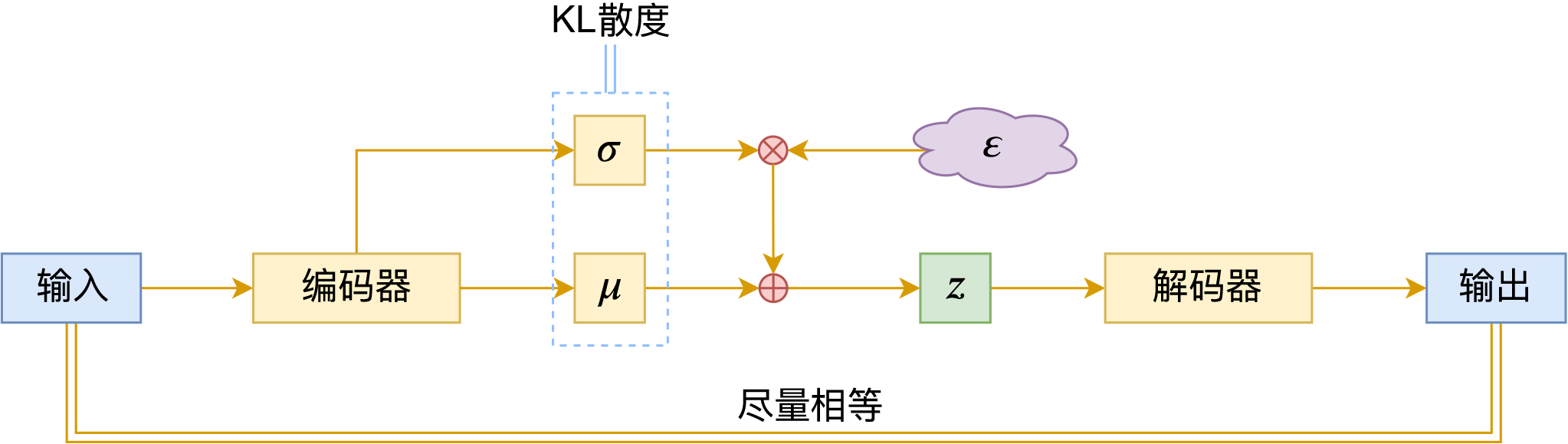
前段时间公司组织技术分享，轮到笔者时，大家希望我讲讲VAE。鉴于之前笔者也写过变分自编码器系列，所以对笔者来说应该也不是特别难的事情，因此就答应了下来，后来仔细一想才觉得犯难：怎么讲才好呢？

变分自编码器示意图

对于VAE来说，之前笔者有两篇比较系统的介绍：《变分自编码器（一）：原来是这么一回事》和《变分自编码器（二）：从贝叶斯观点出发》。后者是纯概率推导，对于不做理论研究的人来说其实没什么意义，也不一定能看得懂；前者虽然显浅一点，但也不妥，因为它是从生成模型的角度来讲的，并没有说清楚“为什么需要VAE”（说白了，VAE可以带来生成模型，但是VAE并不一定就为了生成模型），整体风格也不是特别友好。

笔者想了想，对于大多数不了解但是想用VAE的读者来说，他们应该只希望大概了解VAE的形式，然后想要知道“VAE有什么作用”、“VAE相比AE有什么区别”、“什么场景下需要VAE”等问题的答案，对于这种需求，上面两篇文章都无法很好地满足。于是笔者尝试构思了VAE的一种几何图景，试图从几何角度来描绘VAE的关键特性，在此也跟大家分享一下。

点击阅读全文...

提高模型的泛化性能是机器学习致力追求的目标之一。常见的提高泛化性的方法主要有两种：第一种是添加噪声，比如往输入添加高斯噪声、中间层增加Dropout以及进来比较热门的对抗训练等，对图像进行随机平移缩放等数据扩增手段某种意义上也属于此列；第二种是往loss里边添加正则项，比如$L_1, L_2$惩罚、梯度惩罚等。本文试图探索几种常见的提高泛化性能的手段的关联。

随机噪声

我们记模型为$f(x)$，$\mathcal{D}$为训练数据集合，$l(f(x), y)$为单个样本的loss，那么我们的优化目标是
\begin{equation}\mathop{\text{argmin}}_{\theta} L(\theta)=\mathbb{E}_{(x,y)\sim \mathcal{D}}[l(f(x), y)]\end{equation}
$\theta$是$f(x)$里边的可训练参数。假如往模型输入添加噪声$\varepsilon$，其分布为$q(\varepsilon)$，那么优化目标就变为
\begin{equation}\mathop{\text{argmin}}_{\theta} L_{\varepsilon}(\theta)=\mathbb{E}_{(x,y)\sim \mathcal{D}, \varepsilon\sim q(\varepsilon)}[l(f(x + \varepsilon), y)]\end{equation}
当然，可以添加噪声的地方不仅仅是输入，也可以是中间层，也可以是权重$\theta$，甚至可以是输出$y$（等价于标签平滑），噪声也不一定是加上去的，比如Dropout是乘上去的。对于加性噪声来说，$q(\varepsilon)$的常见选择是均值为0、方差固定的高斯分布；而对于乘性噪声来说，常见选择是均匀分布$U([0,1])$或者是伯努利分布。

添加随机噪声的目的很直观，就是希望模型能学会抵御一些随机扰动，从而降低对输入或者参数的敏感性，而降低了这种敏感性，通常意味着所得到的模型不再那么依赖训练集，所以有助于提高模型泛化性能。

点击阅读全文...

本文介绍来自MIT的一篇ICLR 2020满分论文《Why gradient clipping accelerates training: A theoretical justification for adaptivity》，顾名思义，这篇论文就是分析为什么梯度裁剪能加速深度学习的训练过程。原文很长，公式很多，还有不少研究复杂性的概念，说实话对笔者来说里边的大部分内容也是懵的，不过大概能捕捉到它的核心思想：引入了比常用的L约束更宽松的约束条件，从新的条件出发论证了梯度裁剪的必要性。本文就是来简明分析一下这个过程，供读者参考。

梯度裁剪

假设需要最小化的函数为$f(\theta)$，$\theta$就是优化参数，那么梯度下降的更新公式就是
\begin{equation}\theta \leftarrow \theta-\eta \nabla_{\theta} f(\theta)\end{equation}
其中$\eta$就是学习率。而所谓梯度裁剪（gradient clipping），就是根据梯度的模长来对更新量做一个缩放，比如
\begin{equation}\theta \leftarrow \theta- \eta \nabla_{\theta} f(\theta)\times \min\left\{1, \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert}\right\}\label{eq:clip-1}\end{equation}
或者
\begin{equation}\theta \leftarrow \theta- \eta \nabla_{\theta} f(\theta)\times \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert+\gamma}\label{eq:clip-2}\end{equation}
其中$\gamma > 0$是一个常数。这两种方式都被视为梯度裁剪，总的来说就是控制更新量的模长不超过一个常数，第二种形式也跟RMSProp等自适应学习率优化器相关。此外，更精确地，我们有下面的不等式
\begin{equation}\frac{1}{2}\min\left\{1, \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert}\right\}\leq \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert+\gamma}\leq \min\left\{1, \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert}\right\}\end{equation}
也就是说两者是可以相互控制的，所以其实两者基本是等价的。

点击阅读全文...

前段时间刷Arixv的时候，发现清华大学开源了一个大规模的中文闲聊语料库LCCC（论文链接，项目地址），从开源的文件上来看，这可能是目前开源的数量最大、质量最好的闲聊语料库了，而且还包含了部分多轮对话聊天，总的来说可玩性还是蛮强的。笔者也被它吸引到了，尝试着用它来训练了一个闲聊对话模型，结果看上去还是不错的，在此分享一下自己的经验。

利用单向语言模型做多轮对话示意图

点击阅读全文...