FlatNCE：小批次对比学习效果差的原因竟是浮点误差？

自SimCLR在视觉无监督学习大放异彩以来，对比学习逐渐在CV乃至NLP中流行了起来，相关研究和工作越来越多。标准的对比学习的一个广为人知的缺点是需要比较大的batch_size（SimCLR在batch_size=4096时效果最佳），小batch_size的时候效果会明显降低，为此，后续工作的改进方向之一就是降低对大batch_size的依赖。那么，一个很自然的问题是：标准的对比学习在小batch_size时效果差的原因究竟是什么呢？

近日，一篇名为《Simpler, Faster, Stronger: Breaking The log-K Curse On Contrastive Learners With FlatNCE》对此问题作出了回答：因为浮点误差。看起来真的很让人难以置信，但论文的分析确实颇有道理，并且所提出的改进FlatNCE确实也工作得更好，让人不得不信服。

细微之处 #

接下来，笔者将按照自己的理解和记号来介绍原论文的主要内容。对比学习（Contrastive Learning）就不帮大家详细复习了，大体上来说，对于某个样本$x$，我们需要构建$K$个配对样本$y_1,y_2,\cdots,y_K$，其中$y_t$是正样本而其余都是负样本，然后分别给每个样本对$(x, y_i)$打分，分别记为$s_1,s_2,\cdots,s_K$，对比学习希望拉大正负样本对的得分差，通常直接用交叉熵作为损失：
\begin{equation}-\log \frac{e^{s_t}}{\sum\limits_i e^{s_i}} = \log \left(\sum_i e^{s_i}\right) - s_t = \log \left(1 + \sum_{i\neq t} e^{s_i - s_t}\right)\end{equation}
简单起见，后面都记$\xi=\sum\limits_{i\neq t} e^{s_i - s_t}$。在实践时，正样本通常是数据扩增而来的高相似样本，而负样本则是把batch内所有其他样本都算上，因此大致上可以认为负样本是随机选择的$K-1$个样本。这就说明，正负样本对的差距还是很明显的，因此模型很容易做到$s_t \gg s_i(i\neq t)$，也即$e^{s_i - s_t}\approx 0$。于是，当batch_size比较小的时候（等价于$K$比较小），$\xi$也会相当接近于0，这意味着上述损失函数也会相当接近于0。

损失函数接近于0，通常也意味着梯度接近于0了，然而，这不意味着模型的更新量就很小了。因为当前对比学习用的都是自适应优化器如Adam，它们的更新量大致形式为$\frac{\text{梯度}}{\sqrt{\text{梯度}\otimes\text{梯度}}}\times\text{学习率}$，这就意味着，不管梯度多小，只要它稳定，那么更新量就会保持着$\text{学习率}$的数量级。对比学习正是这样的场景，要想$e^{s_i - s_t}\to 0$，那么就要$s_i - s_t\to -\infty$，但对比学习的打分通常是余弦值除以温度参数，所以它是有界的，$s_i - s_t\to -\infty$是无法实现的，因此经过一定的训练步数后，损失函数将会长期保持接近于0但又大于0的状态。

然而，$\xi$的计算本身就存在浮点误差，当$\xi$很接近于0时，浮点误差可能比精确值还要大，然后$\log(1+\xi)$的计算也会存在浮点误差，再然后梯度的计算也会存在浮点误差，这一系列误差累积下来，很可能导致最后算出来的梯度都接近于随机噪声了，而不能提供有效的更新指引。这就是原论文认为的对比学习在小batch_size时效果明显变差的原因。

变微为著 #

理解了这个原因后，其实也就不难针对性地提出解决方案了。对损失函数做一阶展开我们有：
\begin{equation}\log \left(1 + \sum_{i\neq t} e^{s_i - s_t}\right)\approx \sum_{i\neq t} e^{s_i - s_t}\end{equation}
也就是说，一定训练步数之后，模型相当于以$\xi$为损失函数了。当然，由于$\log(1+\xi)\leq \xi$，即$\xi$是$\log(1+\xi)$的上界，所以就算一开始就以$\xi$为损失函数，结果也没什么差别，现在主要还是解决的问题是$\xi$接近于0而导致了浮点误差问题。刚才说了，自适应优化器的更新量大致上都是$\frac{\text{梯度}}{\sqrt{\text{梯度}\otimes\text{梯度}}}\times\text{学习率}$的形式，这意味着如果我们直接将损失函数乘以一个常数，那么理论上更新量是不会改变的，所以既然$\xi$过小，那么我们就将它乘以一个常数放大就好了。

乘以什么好呢？比较直接的想法是损失函数不能过小，也不能过大，控制在$\mathcal{O}(1)$级别最好，所以我们干脆乘以$\xi$的倒数，也就是以
\begin{equation}\frac{\xi}{\text{sg}(\xi)} = \frac{\sum\limits_{i\neq t} e^{s_i - s_t}}{\text{sg}\left(\sum\limits_{i\neq t} e^{s_i - s_t}\right)}\label{eq:flatnce-1}\end{equation}
为损失函数。这里$\text{sg}$是stop_gradient的意思（原论文称为detach），也就是把分母纯粹当成一个常数，求梯度的时候只需要对分子求。这就是原论文提出的替代方案，称为FlatNCE。

不过，上述带$\text{sg}$算子形式的损失函数毕竟不是我们习惯的形式，我们可以转换一下。观察到：
\begin{equation}\nabla_{\theta}\left(\frac{\xi}{\text{sg}(\xi)}\right) = \frac{\nabla_{\theta}\xi}{\xi} = \nabla_{\theta}\log \xi\end{equation}
也就是说，$\frac{\xi}{\text{sg}(\xi)}$作为损失函数提供的梯度跟$\log \xi$作为损失函数的梯度是一模一样的，因此我们可以把损失函数换为不带$\text{sg}$算子的$\log \xi$：
\begin{equation}\log\left(\sum\limits_{i\neq t} e^{s_i - s_t}\right) = \log\left(\sum\limits_{i\neq t} e^{s_i}\right) - s_t\label{eq:flatnce-2}\end{equation}
相比于交叉熵，上述损失就是在$\text{logsumexp}$运算中去掉了正样本对的得分$s_t$。注意到$\text{logsumexp}$通常可以有效地计算，浮点误差不会占主导，因此我们用上述损失函数取代交叉熵，理论上跟交叉熵是等效的，而实践上在小batch_size时效果比交叉熵要好。此外，需要指出的是，上式结果不一定是非负的，因此换用上述损失函数后在训练过程中出现负的损失值也不需要意外，这是正常现象。

实践真知 #

分析似乎有那么点道理，那么事实是否有效呢？这自然是要靠实验来说话了。不出意料，FlatNCE确实工作得非常好。

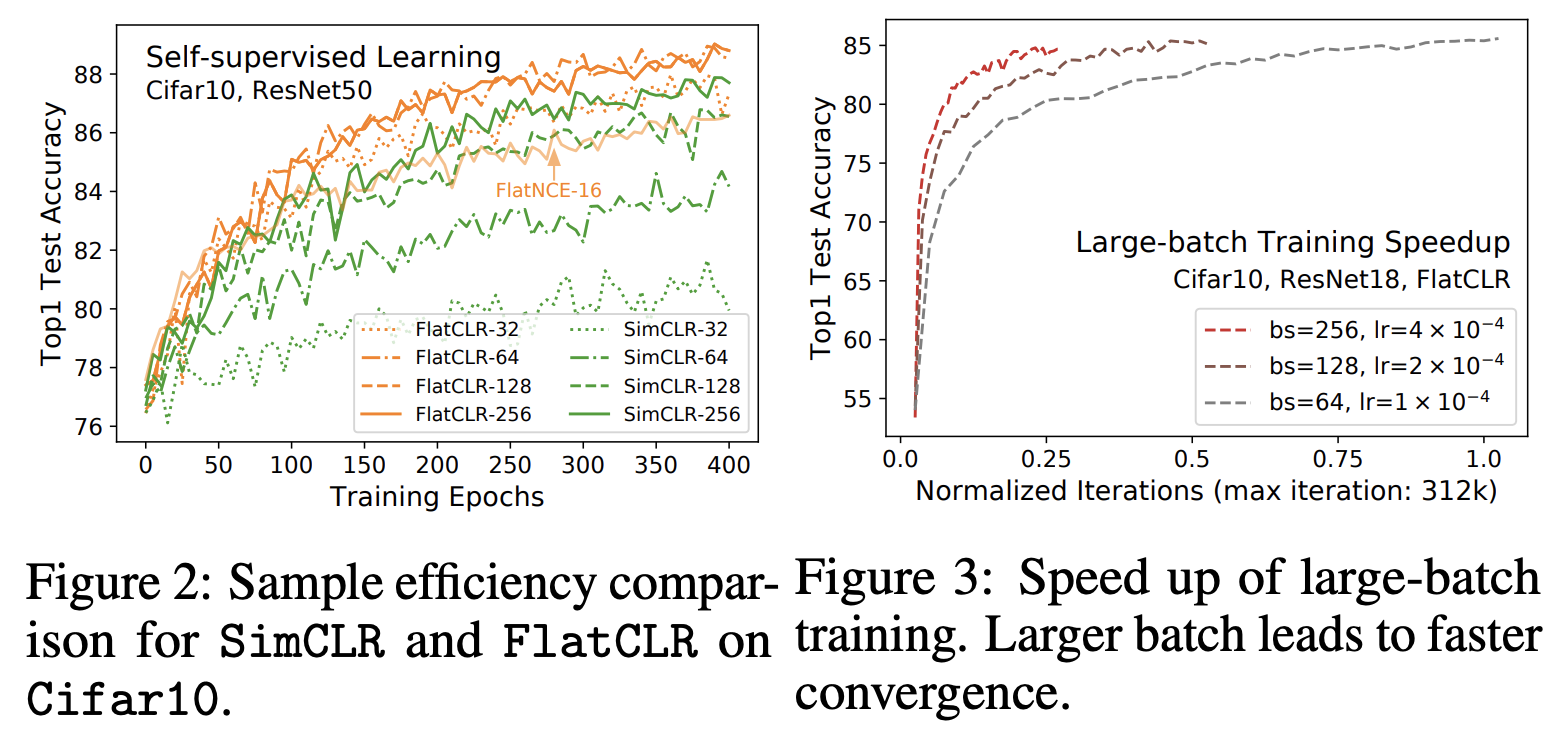
原论文的实验都是CV的，主要是把SimCLR的损失换为FlatNCE进行实验，对应的结果称为FlatCLR。其中，我们最关心的大概是FlatNCE是否真的解决了对大batch_size的依赖问题，下面的图像则作出了肯定回答：

下面则是SimCLR和FlatCLR在各个任务上的结果对比，显示出FlatCLR更好的性能：

吹毛求疵 #

总的来说，原论文的结果非常有创造性，“浮点误差”这一视角非常“刁钻”但也相当精准，让人不得不点赞。

直观来看，原来交叉熵的目标是“正样本得分与负样本得分的差尽量大”，这对于常规的分类问题是没问题的，但对于对比学习来说还不够，因为对比学习目的是学习特征，除了正样本要比负样本得分高这种“粗”特征外，负样本之间也要继续对比以学习更精细的特征；FlatNCE的目标则是“正样本的得分要尽量大，负样本的得分要尽量小”，也即从相对值的学习变成了绝对值的学习，从而使得正负样本拉开一定距离后，依然能够继续优化，而不至于过早停止（对于非自适应优化器），或者让浮点误差带来的噪声占了主导（对于自适应优化器）。

然而，原论文的某些内容设置也不得不让人吐槽。比如，论文花了较大的篇幅讨论互信息的估计，但这跟论文主体并无实质关联，加大了读者的理解难度。当然，paper跟科普不一样，为了使文章更充实而增加额外的理论推导也无可厚非，只是如果能更突出浮点误差部分的分析更好。然后，论文最让我不能理解的地方是直接以$\eqref{eq:flatnce-1}$为最终结果，这种带“stop_gradient”的表述方式虽然算不上难，但也不友好，通常来说这种方式是难以寻求原函数的时候才“不得不”使用的，但FlatNCE显然不是这样。

总结全文 #

本文介绍了对比学习的一个新工作，该工作分析了小批次对比学习时交叉熵的浮点误差问题，指出这可能是小批次对比学习效果差的主要原因，并且针对性地提出了改进的损失函数FlatNCE，实验表明基于FlatNCE的对比学习确实能缓解对大batch_size的依赖，并且能获得更好的效果。

转载到请包括本文地址：https://spaces.ac.cn/archives/8586

更详细的转载事宜请参考：《科学空间FAQ》