超光速飞行

超光速飞行

爱因斯坦理论的信仰者们必须接受一个理论，那就是光速是宇宙中最快的速度，任何物体的速度都不可能超过光速（两束反向发射的光，它们的相对速度依然是c，而不是2c）。

但是，却有一个不容否定的事实，天文学家的确观测到了运行速度大于光速的天体。这是怎么回事呢？爱因斯坦错了？相对论有误？还是有其他不为我们知道的秘密？

不过要是想从这个事实推翻相对论是不大可能的，因为爱因斯坦的信仰者们从简单的几何定理出发，就解释了这个现象。

首先我们得反问一下自己：我们能够观测到速度吗？显然不能，我们能够测量的只是路程和时间，我们无法观测到速度，我们只是间接使用$v=s/t$来得到速度。这样一来，问题就出在了s和t上面了。有什么问题呢？请看下图

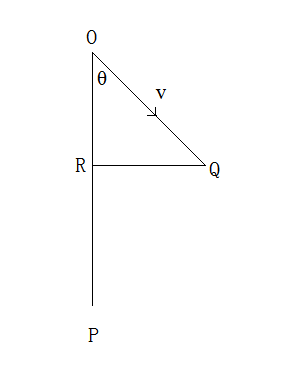
超光速-示意图

超光速-示意图

P为观测者，O为运动的天体，物体以v速度向OQ方向移动，OP为视方向，RQ为横向。设OQ=r，则$t=r/v$，而我们看到天体从R运行到Q的时间为$r/v-\frac{r \cos\theta}{c}$。于是我们看到的横向速度为$v'=\frac{r \sin\theta}{r/v-\frac{r \cos\theta}{c}}=\frac{cv\cdot \sin\theta}{c-v \cos\theta}$。计算$\frac{dv'}{d\theta}=0$不难得出，当$c\cdot \cos\theta=v$时，取最大值，此时
$$v'=\frac{v}{\sqrt{1-\frac{v^2}{c^2}}}$$

当$v->c$时，$v'->\infty$。所以我们有可能看到运动速度为任意大的天体！

转载到请包括本文地址：https://spaces.ac.cn/archives/671

更详细的转载事宜请参考：《科学空间FAQ》

如果您还有什么疑惑或建议，欢迎在下方评论区继续讨论。

如果您觉得本文还不错，欢迎分享/打赏本文。打赏并非要从中获得收益，而是希望知道科学空间获得了多少读者的真心关注。当然，如果你无视它，也不会影响你的阅读。再次表示欢迎和感谢！

如果您需要引用本文，请参考：

苏剑林. (Jun. 05, 2010). 《眼见未必为实——“视超光速”现象的产生 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/671

@online{kexuefm-671,
        title={眼见未必为实——“视超光速”现象的产生},
        author={苏剑林},
        year={2010},
        month={Jun},
        url={\url{https://spaces.ac.cn/archives/671}},
}