【理解黎曼几何】1. 一条几何之路
By 苏剑林 | 2016-10-14 | 81712位读者 | 引用一个月没更新了,这个月花了不少时间在黎曼几何的理解方面,有一些体会,与大家分享。记得当初孟岩写的《理解矩阵》,和笔者所写的《新理解矩阵》,读者反响都挺不错的,这次沿用了这个名称,称之为《理解黎曼几何》。
黎曼几何是研究内蕴几何的几何分支。通俗来讲,就是我们可能生活在弯曲的空间中,比如一只生活在二维球面的蚂蚁,作为生活在弯曲空间中的个体,我们并没有足够多的智慧去把我们的弯曲嵌入到更高维的空间中去研究,就好比蚂蚁只懂得在球面上爬,不能从“三维空间的曲面”这一观点来认识球面,因为球面就是它们的世界。因此,我们就有了内蕴几何,它告诉我们,即便是身处弯曲空间中,我们依旧能够测量长度、面积、体积等,我们依旧能够算微分、积分,甚至我们能够发现我们的空间是弯曲的!也就是说,身处球面的蚂蚁,只要有足够的智慧,它们就能发现曲面是弯曲的——跟哥伦布环球航行那样——它们朝着一个方向走,最终却回到了起点,这就可以断定它们自身所处的空间必然是弯曲的——这个发现不需要用到三维空间的知识。
梯度流:探索通向最小值之路
By 苏剑林 | 2023-06-16 | 32165位读者 | 引用在这篇文章中,我们将探讨一个被称为“梯度流(Gradient Flow)”的概念。简单来说,梯度流是将我们在用梯度下降法中寻找最小值的过程中的各个点连接起来,形成一条随(虚拟的)时间变化的轨迹,这条轨迹便被称作“梯度流”。在文章的后半部分,我们将重点讨论如何将梯度流的概念扩展到概率空间,从而形成“Wasserstein梯度流”,为我们理解连续性方程、Fokker-Planck方程等内容提供一个新的视角。
梯度下降
假设我们想搜索光滑函数$f(\boldsymbol{x})$的最小值,常见的方案是梯度下降(Gradient Descent),即按照如下格式进行迭代:
\begin{equation}\boldsymbol{x}_{t+1} = \boldsymbol{x}_t -\alpha \nabla_{\boldsymbol{x}_t}f(\boldsymbol{x}_t)\label{eq:gd-d}\end{equation}
如果$f(\boldsymbol{x})$关于$\boldsymbol{x}$是凸的,那么梯度下降通常能够找到最小值点;相反,则通常只能收敛到一个“驻点”——即梯度为0的点,比较理想的情况下能收敛到一个极小值(局部最小值)点。这里没有对极小值和最小值做严格区分,因为在深度学习中,即便是收敛到一个极小值点也是很难得的了。
低秩近似之路(一):伪逆
By 苏剑林 | 2024-09-15 | 19676位读者 | 引用可能很多读者跟笔者一样,对矩阵的低秩近似有种熟悉而又陌生的感觉。熟悉是因为,低秩近似的概念和意义都不难理解,加之目前诸如LoRA等基于低秩近似的微调技术遍地开花,让低秩近似的概念在耳濡目染间就已经深入人心;然而,低秩近似所覆盖的内容非常广,在低秩近似相关的论文中时常能看到一些不熟悉但又让我们叹为观止的新技巧,这就导致了一种似懂非懂的陌生感。
因此,在这个系列文章中,笔者将试图系统梳理一下矩阵低秩近似相关的理论内容,以补全对低秩近似的了解。而在第一篇文章中,我们主要介绍低秩近似系列中相对简单的一个概念——伪逆。
优化视角
伪逆(Pseudo Inverse),也称“广义逆(Generalized Inverse)”,顾名思义就是“广义的逆矩阵”,它实际上是“逆矩阵”的概念对于不可逆矩阵的推广。
低秩近似之路(二):SVD
By 苏剑林 | 2024-10-01 | 16650位读者 | 引用上一篇文章中我们介绍了“伪逆”,它关系到给定矩阵$\boldsymbol{M}$和$\boldsymbol{A}$(或$\boldsymbol{B}$)时优化目标$\Vert \boldsymbol{A}\boldsymbol{B} - \boldsymbol{M}\Vert_F^2$的最优解。这篇文章我们来关注$\boldsymbol{A},\boldsymbol{B}$都不给出时的最优解,即
\begin{equation}\mathop{\text{argmin}}_{\boldsymbol{A},\boldsymbol{B}}\Vert \boldsymbol{A}\boldsymbol{B} - \boldsymbol{M}\Vert_F^2\label{eq:loss-ab}\end{equation}
其中$\boldsymbol{A}\in\mathbb{R}^{n\times r}, \boldsymbol{B}\in\mathbb{R}^{r\times m}, \boldsymbol{M}\in\mathbb{R}^{n\times m},r < \min(n,m)$。说白了,这就是要寻找矩阵$\boldsymbol{M}$的“最优$r$秩近似(秩不超过$r$的最优近似)”。而要解决这个问题,就需要请出大名鼎鼎的“SVD(奇异值分解)”了。虽然本系列把伪逆作为开篇,但它的“名声”远不如SVD,听过甚至用过SVD但没听说过伪逆的应该大有人在,包括笔者也是先了解SVD后才看到伪逆。
接下来,我们将围绕着矩阵的最优低秩近似来展开介绍SVD。
结论初探
对于任意矩阵$\boldsymbol{M}\in\mathbb{R}^{n\times m}$,都可以找到如下形式的奇异值分解(SVD,Singular Value Decomposition):
\begin{equation}\boldsymbol{M} = \boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}\end{equation}
时空之章:将Attention视为平方复杂度的RNN
By 苏剑林 | 2024-03-18 | 44802位读者 | 引用近年来,RNN由于其线性的训练和推理效率,重新吸引了不少研究人员和用户的兴趣,隐约有“文艺复兴”之势,其代表作有RWKV、RetNet、Mamba等。当将RNN用于语言模型时,其典型特点就是每步生成都是常数的空间复杂度和时间复杂度,从整个序列看来就是常数的空间复杂度和线性的时间复杂度。当然,任何事情都有两面性,相比于Attention动态增长的KV Cache,RNN的常数空间复杂度通常也让人怀疑记忆容量有限,在Long Context上的效果很难比得上Attention。
在这篇文章中,我们表明Causal Attention可以重写成RNN的形式,并且它的每一步生成理论上也能够以$\mathcal{O}(1)$的空间复杂度进行(代价是时间复杂度非常高,远超平方级)。这表明Attention的优势(如果有的话)是靠计算堆出来的,而不是直觉上的堆内存,它跟RNN一样本质上都是常数量级的记忆容量(记忆瓶颈)。
“闭门造车”之多模态思路浅谈(一):无损输入
By 苏剑林 | 2024-02-21 | 147139位读者 | 引用这篇文章分享一下笔者关于多模态模型架构的一些闭门造车的想法,或者说一些猜测。
最近Google的Gemini 1.5和OpenAI的Sora再次点燃了不少人对多模态的热情,只言片语的技术报告也引起了大家对其背后模型架构的热烈猜测。不过,本文并非是为了凑这个热闹才发出来的,事实上其中的一些思考由来已久,最近才勉强捋顺了一下,遂想写出来跟大家交流一波,刚好碰上了两者的发布。
事先声明,“闭门造车”一词并非自谦,笔者的大模型实践本就“乏善可陈”,而多模态实践更是几乎“一片空白”,本文确实只是根据以往文本生成和图像生成的一些经验所做的“主观臆测”。
问题背景
首先简化一下问题,本文所讨论的多模态,主要指图文混合的双模态,即输入和输出都可以是图文。可能有不少读者的第一感觉是:多模态模型难道不也是烧钱堆显卡,Transformer“一把梭”,最终“大力出奇迹”吗?
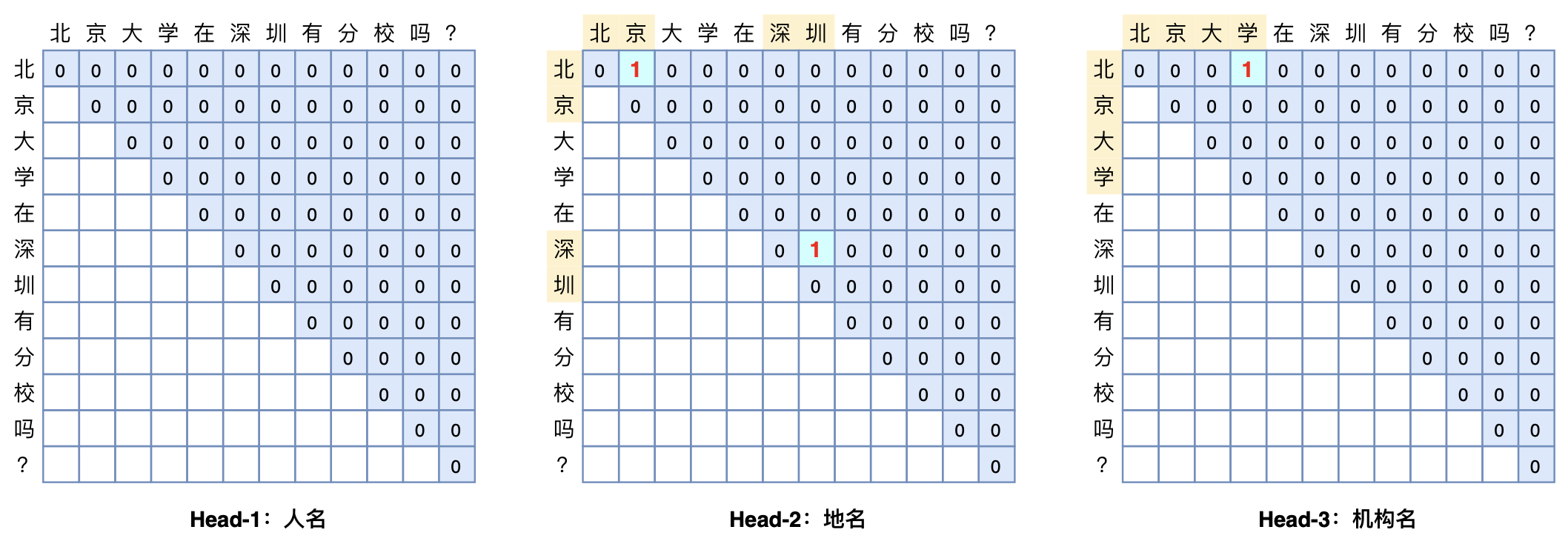
GlobalPointer:用统一的方式处理嵌套和非嵌套NER
By 苏剑林 | 2021-05-01 | 308520位读者 | 引用(注:本文的相关内容已整理成论文《Global Pointer: Novel Efficient Span-based Approach for Named Entity Recognition》,如需引用可以直接引用英文论文,谢谢。)
本文将介绍一个称为GlobalPointer的设计,它利用全局归一化的思路来进行命名实体识别(NER),可以无差别地识别嵌套实体和非嵌套实体,在非嵌套(Flat NER)的情形下它能取得媲美CRF的效果,而在嵌套(Nested NER)情形它也有不错的效果。还有,在理论上,GlobalPointer的设计思想就比CRF更合理;而在实践上,它训练的时候不需要像CRF那样递归计算分母,预测的时候也不需要动态规划,是完全并行的,理想情况下时间复杂度是$\mathcal{O}(1)$!
简单来说,就是更漂亮、更快速、更强大!真有那么好的设计吗?不妨继续看看。
线性Transformer应该不是你要等的那个模型
By 苏剑林 | 2021-08-09 | 101823位读者 | 引用在本博客中,我们已经多次讨论过线性Attention的相关内容。介绍线性Attention的逻辑大体上都是:标准Attention具有$\mathcal{O}(n^2)$的平方复杂度,是其主要的“硬伤”之一,于是我们$\mathcal{O}(n)$复杂度的改进模型,也就是线性Attention。有些读者看到线性Attention的介绍后,就一直很期待我们发布基于线性Attention的预训练模型,以缓解他们被BERT的算力消耗所折腾的“死去活来”之苦。
然而,本文要说的是:抱有这种念头的读者可能要失望了,标准Attention到线性Attention的转换应该远远达不到你的预期,而BERT那么慢的原因也并不是因为标准Attention的平方复杂度。
BERT之反思
按照直观理解,平方复杂度换成线性复杂度不应该要“突飞猛进”才对嘛?怎么反而“远远达不到预期”?出现这个疑惑的主要原因,是我们一直以来都没有仔细评估一下常规的Transformer模型(如BERT)的整体计算量。









最近评论