在对GAN的学习和思考过程中，我发现我不仅学习到了一种有效的生成模型，而且它全面地促进了我对各种模型各方面的理解，比如模型的优化和理解视角、正则项的意义、损失函数与概率分布的联系、概率推断等等。GAN不单单是一个“造假的玩具”，而是具有深刻意义的概率模型和推断方法。

作为事后的总结，我觉得对GAN的理解可以粗糙地分为三个阶段：

1、样本阶段：在这个阶段中，我们了解了GAN的“鉴别者-造假者”诠释，懂得从这个原理出发来写出基本的GAN公式（如原始GAN、LSGAN），比如判别器和生成器的loss，并且完成简单GAN的训练；同时，我们知道GAN有能力让图片更“真”，利用这个特性可以把GAN嵌入到一些综合模型中。

2、分布阶段：在这个阶段中，我们会从概率分布及其散度的视角来分析GAN，典型的例子是WGAN和f-GAN，同时能基本理解GAN的训练困难问题，比如梯度消失和mode collapse等，甚至能基本地了解变分推断，懂得自己写出一些概率散度，继而构造一些新的GAN形式。

3、动力学阶段：在这个阶段中，我们开始结合优化器来分析GAN的收敛过程，试图了解GAN是否能真的达到理论的均衡点，进而理解GAN的loss和正则项等因素如何影响的收敛过程，由此可以针对性地提出一些训练策略，引导GAN模型到达理论均衡点，从而提高GAN的效果。

事实上，不仅仅是GAN，对于一般的模型理解，也可以大致上分为这三个阶段。当然也许有热衷于几何解释或其他诠释的读者会不同意第二点，觉得没必要非得概率分布的角度来理解。但事实上几何视角和概率视角都有一定的相通之处，而本文所写的三个阶段只是一个粗糙的总结，简单来说就是从局部到整体，然后再到优化器。

而本文主要聚焦于GAN的第三个阶段：GAN的动力学。

基本原理 #

一般情况下，GAN可以表示为一个min-max过程，记作
\begin{equation}\min_G \max_D L(G,D)\end{equation}
其中$\max\limits_D L(G,D)$这一步定义了一个概率散度而$\min\limits_G$这一步则在最小化散度，相关的讨论也可以参考本网站的《f-GAN简介：GAN模型的生产车间》和《不用L约束又不会梯度消失的GAN，了解一下？》。

注意，从理论上讲，这个min-max过程是有序的，即需要彻底地、精确地完成$\max\limits_D$这一步，然后才去$\min\limits_G$。但是很显然，实际训练GAN时我们做不到这一点，我们都是$D,G$交替训练的，理想情况下我们还希望$D,G$每次只各自训练一次，这样训练效率最高，而这样的训练方法对应于一个动力系统。

动力系统 #

在我们的“从动力学角度看优化算法”系列中，我们将梯度下降看成是在数学求解动力系统（也就是一个常微分方程组，简称ODEs）
\begin{equation}\dot{\boldsymbol{\theta}} = - \nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta})\end{equation}
其中$L(\boldsymbol{\theta})$是模型的loss，而$\boldsymbol{\theta}$是模型的参数。如果考虑随机性，那么则需要加上一个噪声项，变成一个随机微分方程，但本文我们不考虑随机性，这不影响我们对局部收敛性的分析。假定读者已经熟悉了这种转换，下面就来讨论GAN对应的过程。

GAN是一个min-max的过程，换句话说，一边是梯度下降，另一边是梯度上升，假设$\boldsymbol{\varphi}$是判别器的参数，$\boldsymbol{\theta}$是生成器的参数，那么GAN对应的动力系统是
\begin{equation}\begin{pmatrix}\dot{\boldsymbol{\varphi}}\\ \dot{\boldsymbol{\theta}}\end{pmatrix} = \begin{pmatrix} \nabla_{\boldsymbol{\varphi}} L(\boldsymbol{\varphi},\boldsymbol{\theta})\\ - \nabla_{\boldsymbol{\theta}} L(\boldsymbol{\varphi},\boldsymbol{\theta})\end{pmatrix}\end{equation}
当然，对于更一般的GAN，有时候两个$L$会稍微不一样：
\begin{equation}\begin{pmatrix}\dot{\boldsymbol{\varphi}}\\ \dot{\boldsymbol{\theta}}\end{pmatrix} = \begin{pmatrix} \nabla_{\boldsymbol{\varphi}} L_1(\boldsymbol{\varphi},\boldsymbol{\theta})\\ - \nabla_{\boldsymbol{\theta}} L_2(\boldsymbol{\varphi},\boldsymbol{\theta})\end{pmatrix}\end{equation}
不管是哪一种，右端两项都是一正一负，而就是因为这一正一负的差异，导致了GAN训练上的困难～我们下面就逐步认识到这一点。

相关工作 #

将GAN的优化过程视为一个（随机）动力系统，基于这个观点进行研究分析的文献已有不少，我读到的包括《The Numerics of GANs》、《GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium》、《Gradient descent GAN optimization is locally stable》、《Which Training Methods for GANs do actually Converge?》，而本文只不过是前辈大牛们的工作的一个学习总结。

在这几篇文献中，大家可能比较熟悉的是第二篇，因为就是第二篇提出了TTUR的GAN训练策略以及提出了FID作为GAN的性能指标，而这篇论文的理论基础也是将GAN的优化看成前述的随机动力系统，然后引用了随机优化中的一个定理，得出可以给生成器和判别器分别使用不同的学习率（TTUR）。而其余几篇，都是直接将GAN的优化看成确定性的动力系统（ODEs），然后用分析ODEs的方法来分析GAN。由于ODEs的理论分析/数值求解都说得上相当成熟，因此可以直接将很多ODEs的结论用到GAN中。

Dirac GAN #

本文的思路和结果主要参考《Which Training Methods for GANs do actually Converge?》，这篇论文的主要贡献如下：

1、提出了Dirac GAN的概念，借助它可以快速地对GAN的性态有个基本的认识；

2、完整地分析了带零中心梯度惩罚的WGAN（也是WGAN-div）的局部收敛性；

3、利用零中心梯度惩罚的WGAN训练了1024的人脸、256的LSUN生成，并且不需要像PGGAN那样渐进式训练。

由于实验设备限制，第三点我们难以复现，而第二点涉及到比较复杂的理论分析，我们也不作过多讨论，有兴趣攻克的读者直接读原论文即可。本文主要关心第一点：Dirac GAN。

所谓Dirac GAN，就是考虑真样本分布只有一个样本点的情况下，待研究的GAN模型的表现。假设真实样本点是零向量$\boldsymbol{0}$，而假样本为$\boldsymbol{\theta}$，其实它也代表着生成器的参数；而判别器采用最简单的线性模型，即（加激活函数之前）为$D(\boldsymbol{x})=\boldsymbol{x}\cdot \boldsymbol{\varphi}$，其中$\boldsymbol{\varphi}$代表着判别器的参数。Dirac GAN就是考虑这样的一个极简模型下，假样本最终能否收敛到真样本，也就是说$\boldsymbol{\theta}$最终能否收敛到$\boldsymbol{0}$。

然而，原论文只考虑了样本点的维度是一维的情形，即$\boldsymbol{0},\boldsymbol{\theta},\boldsymbol{\varphi}$都是标量，但本文后面的案例表明，对于某些例子，一维Dirac GAN不足以揭示它的收敛性态，一般情况下至少需要2维Dirac GAN才能较好地分析一个GAN的渐近收敛性。

常见GAN分析 #

上一节我们给出了Dirac GAN的基本概念，指出它可以帮助我们对GAN的收敛性态有个快速的认识。在这部分内容中，我们通过分析若干常见GAN，来更详细地表明Dirac GAN怎么做到这一点。

Vanilla GAN #

Vanilla GAN，或者叫做原始GAN、标准GAN，它就是指Goodfellow最早提出来的GAN，它有saturating和non-saturating两种形式。作为例子，我们来分析比较常用的non-saturating形式：
\begin{equation}\begin{aligned}&\min_D \mathbb{E}_{\boldsymbol{x}\sim p(\boldsymbol{x})}[-\log D(\boldsymbol{x})]+\mathbb{E}_{\boldsymbol{x}\sim q(\boldsymbol{x})}[-\log (1-D(\boldsymbol{x}))]\\
&\min_G \mathbb{E}_{\boldsymbol{z}\sim q(\boldsymbol{z})}[-\log D(G(\boldsymbol{z}))]
\end{aligned}\end{equation}
这里的$p(\boldsymbol{x}),q(\boldsymbol{x})$分别是真假样本分布，而$q(\boldsymbol{z})$是噪声分布，$D(\boldsymbol{x})$用sigmoid激活。对应到Dirac GAN下，那就简单得多，因为真样本只有一个点而且为$\boldsymbol{0}$，所以判别器的loss只有一项，而判别器可以完全写出为$\boldsymbol{\theta}\cdot \boldsymbol{\varphi}$，其中$\boldsymbol{\theta}$也就是假样本，或者说生成器，最终结果是：
\begin{equation}\begin{aligned}&\min_{\boldsymbol{\varphi}} -\log (1-\sigma(\boldsymbol{\theta}\cdot \boldsymbol{\varphi}))\\
&\min_{\boldsymbol{\theta}} -\log \sigma(\boldsymbol{\theta}\cdot \boldsymbol{\varphi})
\end{aligned}\end{equation}
对应的动力系统是：
\begin{equation}\begin{pmatrix}\dot{\boldsymbol{\varphi}}\\ \dot{\boldsymbol{\theta}}\end{pmatrix} = \begin{pmatrix} \nabla_{\boldsymbol{\varphi}} \log (1-\sigma(\boldsymbol{\theta}\cdot \boldsymbol{\varphi}))\\ \nabla_{\boldsymbol{\theta}} \log \sigma(\boldsymbol{\theta}\cdot \boldsymbol{\varphi})\end{pmatrix} = \begin{pmatrix} - \sigma(\boldsymbol{\theta}\cdot \boldsymbol{\varphi}) \boldsymbol{\theta}\\ (1 - \sigma(\boldsymbol{\theta}\cdot \boldsymbol{\varphi}))\boldsymbol{\varphi}\end{pmatrix}\end{equation}
这个动力系统的均衡点（让右端直接等于0）是$\boldsymbol{\varphi}=\boldsymbol{\theta}=\boldsymbol{0}$，也就是假样本变成了真样本。但问题是从一个初始点出发，该初始点最终能否收敛到均衡点却是个未知数。

数值求解的non-saturating的Dirac GAN的优化轨迹（二维情形），可以发现它确实只是在均衡点（红色点）周围振荡，不收敛

数值求解的non-saturating的Dirac GAN的优化轨迹（二维情形），可以发现它确实只是在均衡点（红色点）周围振荡，不收敛

为了做出判断，我们假设系统已经跑到了均衡点附近，即$\boldsymbol{\varphi}\approx \boldsymbol{0}, \boldsymbol{\theta}\approx \boldsymbol{0}$，那么可以近似地线性展开：
\begin{equation}\begin{pmatrix}\dot{\boldsymbol{\varphi}}\\ \dot{\boldsymbol{\theta}}\end{pmatrix} = \begin{pmatrix} - \sigma(\boldsymbol{\theta}\cdot \boldsymbol{\varphi}) \boldsymbol{\theta}\\ (1 - \sigma(\boldsymbol{\theta}\cdot \boldsymbol{\varphi}))\boldsymbol{\varphi}\end{pmatrix} \approx \begin{pmatrix} - \boldsymbol{\theta} / 2\\ \boldsymbol{\varphi} / 2\end{pmatrix}\end{equation}
最终近似地有
\begin{equation}\ddot{\boldsymbol{\theta}}\approx - \boldsymbol{\theta} / 4\end{equation}
学过常微分方程的同学都知道，这是最简单的线性常微分方程之一，只要初始值不是$\boldsymbol{0}$，那么它的解是一个周期解，也就是说并不会出现$\boldsymbol{\theta}\to \boldsymbol{0}$的特性。换句话说，对于non-saturating的Vanilla GAN，哪怕模型的初始化已经相当接近均衡点了，但是它始终不会收敛到均衡点，而是在均衡点附近振荡。数值模拟的结果则进一步证明了这一点。

事实上，类似的结果出现在任何形式的f-GAN中，即以f散度为基础的所有GAN都存在同样的问题（不计正则项），即它们会慢慢收敛到均衡点附近，最终都只是在均衡点附近振荡，无法完全收敛到均衡点。

这里再重复一下逻辑：我们知道系统的理论均衡点确实是我们想要的，但是从任意一个初值（相当于模型的初始化）出发，经过迭代后最终是否能跑到理论均衡点（相当于理想地完成GAN的训练），这无法很显然地得到结果，至少需要在均衡点附近做线性展开，分析它的收敛性，这就是说所谓的局部渐近收敛性态。

WGAN #

f-GAN败下阵来了，那WGAN又如何呢？它又能否收敛到理想的均衡点呢？

WGAN的一般形式是
\begin{equation}\min_G \max_{D, \Vert D\Vert_L\leq 1} \mathbb{E}_{\boldsymbol{x}\sim p(\boldsymbol{x})}[D(\boldsymbol{x})] - \mathbb{E}_{\boldsymbol{z}\sim q(\boldsymbol{z})}[D(G(\boldsymbol{z}))]\end{equation}
对应到Dirac GAN，$D(\boldsymbol{x})=\boldsymbol{x}\cdot \boldsymbol{\varphi}$，而$\Vert D\Vert_L\leq 1$可以由$\Vert \boldsymbol{\varphi}\Vert=1$来保证（$\Vert\cdot\Vert$是$l_2$模长），换言之，$D(\boldsymbol{x})$加上L约束后为$D(\boldsymbol{x})=\boldsymbol{x}\cdot \boldsymbol{\varphi} / \Vert\boldsymbol{\varphi}\Vert$，那么WGAN对应的Dirac GAN为
\begin{equation}\min_{\boldsymbol{\theta}}\max_{\boldsymbol{\varphi}} \frac{-\boldsymbol{\theta}\cdot \boldsymbol{\varphi}}{\Vert\boldsymbol{\varphi}\Vert}\end{equation}
对应的动力系统是：
\begin{equation}\begin{pmatrix}\dot{\boldsymbol{\varphi}}\\ \dot{\boldsymbol{\theta}}\end{pmatrix} = \begin{pmatrix} \nabla_{\boldsymbol{\varphi}} (-\boldsymbol{\theta}\cdot \boldsymbol{\varphi} / \Vert \boldsymbol{\varphi}\Vert)\\ \nabla_{\boldsymbol{\theta}} (\boldsymbol{\theta}\cdot \boldsymbol{\varphi} / \Vert \boldsymbol{\varphi}\Vert)\end{pmatrix} = \begin{pmatrix} -\boldsymbol{\theta} / \Vert \boldsymbol{\varphi}\Vert + (\boldsymbol{\theta}\cdot \boldsymbol{\varphi})\boldsymbol{\varphi} / \Vert \boldsymbol{\varphi}\Vert^3\\ \boldsymbol{\varphi} / \Vert \boldsymbol{\varphi}\Vert\end{pmatrix}\end{equation}
我们主要关心$\boldsymbol{\theta}$是否会趋于$\boldsymbol{0}$，可以引入类似前一节的线性展开，但是由于$\Vert \boldsymbol{\varphi}\Vert$在分母，所以讨论起来会比较困难。最干脆的方法是直接数值求解这个方程组，结果如下图：

数值求解的WGAN对应的Dirac GAN的优化轨迹（二维情形），可以发现它确实只是在均衡点（红色点）周围振荡，不收敛

数值求解的WGAN对应的Dirac GAN的优化轨迹（二维情形），可以发现它确实只是在均衡点（红色点）周围振荡，不收敛

可以看到，结果依然是在均衡点附近振荡，并没能够达到均衡点。这个结果表明了，WGAN（同时自然也包括了谱归一化）都没有局部收敛性，哪怕已经跑到了均衡点附近，依然无法准确地落在均衡点上。

（注：稍加分析就能得出，如果只考虑一维的Dirac GAN，那么将无法分析本节的WGAN和后面的GAN-QP，这就是只考虑一维情形的局限性。）

WGAN-GP #

大家可能会疑惑，前面不是讨论了WGAN了吗，怎么还要讨论WGAN-GP？

事实上，从优化角度看，前面所说的WGAN和WGAN-GP是两类不一样的模型。前面的WGAN是指事先在判别器上加上L约束（比如谱归一化），然后进行对抗学习；这里的WGAN-GP指的是判别器不加L约束，而是通过梯度惩罚项（Gradient Penalty）来迫使判别器具有L约束。这里讨论的梯度惩罚有两种，第一种是《Improved Training of Wasserstein GANs》提出来的“以1为中心的梯度惩罚”，第二种是《Wasserstein Divergence for GANs》、《Which Training Methods for GANs do actually Converge?》等文章提倡的“以0为中心的梯度惩罚”。下面我们会对比这两种梯度惩罚的不同表现。

梯度惩罚的一般形式是：
\begin{equation}\begin{aligned}&\min_{D} \mathbb{E}_{\boldsymbol{x}\sim q(\boldsymbol{x})}[D(\boldsymbol{x})] - \mathbb{E}_{\boldsymbol{x}\sim p(\boldsymbol{x})}[D(\boldsymbol{x})] + \lambda \mathbb{E}_{\boldsymbol{x}\sim r(\boldsymbol{x})}\left[(\left\Vert\nabla_{\boldsymbol{x}}D(\boldsymbol{x})\right\Vert - c)^2\right]\\
&\min_{G} \mathbb{E}_{\boldsymbol{z}\sim q(\boldsymbol{z})}[-D(G(\boldsymbol{z}))] \end{aligned}\end{equation}
其中$c=0$或$c=1$，而$r(\boldsymbol{x})$是$p(\boldsymbol{x})$和$q(\boldsymbol{x})$的某个衍生分布，一般直接取真样本分布、假样本分布或者真假样本插值。

对于Dirac GAN来说：
\begin{equation}\nabla_{\boldsymbol{x}}D(\boldsymbol{x}) = \nabla_{\boldsymbol{x}}(\boldsymbol{x}\cdot\boldsymbol{\varphi})=\boldsymbol{\varphi}\end{equation}
也就是说它跟$\boldsymbol{x}$没关系，所以$r(\boldsymbol{x})$怎么取都不影响结果了。因此，WGAN-GP版本的Dirac GAN形式为：
\begin{equation}\begin{aligned}&\min_{\boldsymbol{\varphi}} \boldsymbol{\theta}\cdot\boldsymbol{\varphi} + \lambda (\left\Vert \boldsymbol{\varphi}\right\Vert - c)^2\\
&\min_{\boldsymbol{\theta}} -\boldsymbol{\theta}\cdot\boldsymbol{\varphi}\end{aligned}\end{equation}
对应的动力系统是：
\begin{equation}\begin{pmatrix}\dot{\boldsymbol{\varphi}}\\ \dot{\boldsymbol{\theta}}\end{pmatrix} = \begin{pmatrix} \nabla_{\boldsymbol{\varphi}} (-\boldsymbol{\theta}\cdot\boldsymbol{\varphi} - \lambda (\left\Vert \boldsymbol{\varphi}\right\Vert - c)^2)\\ \nabla_{\boldsymbol{\theta}} (\boldsymbol{\theta}\cdot\boldsymbol{\varphi})\end{pmatrix} = \begin{pmatrix} -\boldsymbol{\theta} - 2\lambda (1 - c / \Vert \boldsymbol{\varphi}\Vert) \boldsymbol{\varphi} \\ \boldsymbol{\varphi} \end{pmatrix}\end{equation}
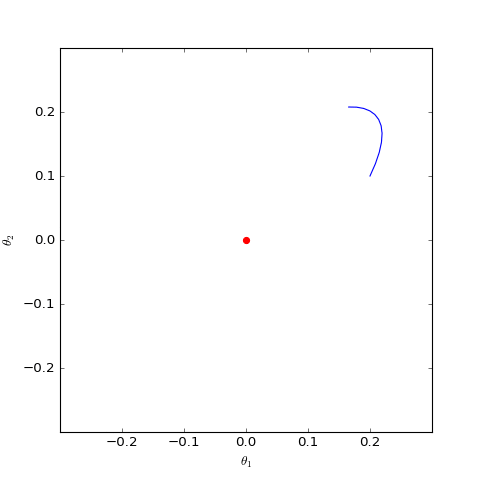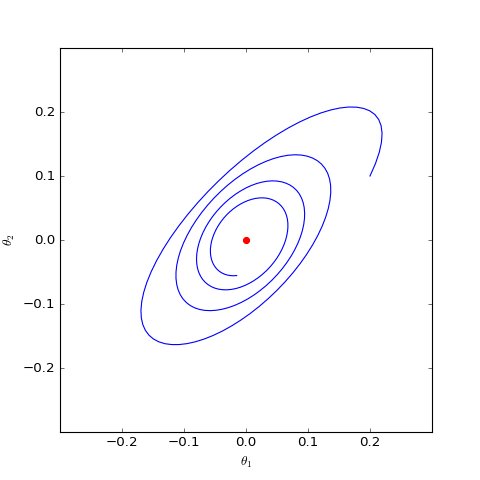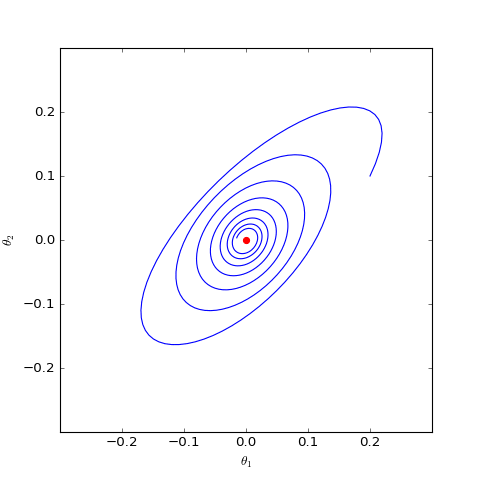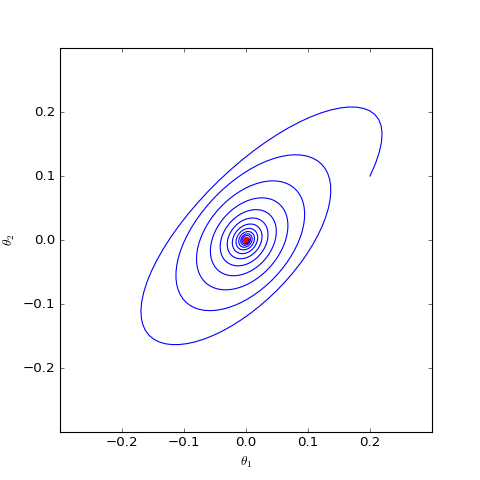
下面我们分别观察$c=0,c=1$时$\boldsymbol{\theta}$是否会趋于$\boldsymbol{0}$，当$c=0$时其实只是一个线性常微分方程组，可以解析求解，但$c=1$时比较复杂，因此简单起见，我们还是直接用数值求解的方式：

数值求解的WGAN-GP(c=0)对应的Dirac GAN的优化轨迹（二维情形），可以发现它能够渐近收敛到均衡点（红色点）

数值求解的WGAN-GP(c=0)对应的Dirac GAN的优化轨迹（二维情形），可以发现它能够渐近收敛到均衡点（红色点）

数值求解的WGAN-GP(c=1)对应的Dirac GAN的优化轨迹（二维情形），可以发现它确实只是在均衡点（红色点）周围振荡，不收敛

数值求解的WGAN-GP(c=1)对应的Dirac GAN的优化轨迹（二维情形），可以发现它确实只是在均衡点（红色点）周围振荡，不收敛

上图是在同样的初始条件（初始化）下，$c=0,c=1$的梯度惩罚的不同表现，两图的其他参数都一样。可以看到，加入“以1为中心的梯度惩罚”后，Dirac GAN并没有渐近收敛到原点，反而只是收敛到一个圆上；而加入“以0为中心的梯度惩罚”则可以达到这个目的。这说明早期提出的梯度惩罚项确实是存在一些缺陷的，而“以0为中心的梯度惩罚”在收敛性态上更好。尽管上述仅仅对Dirac GAN做了分析，但结论具有代表性，因为关于0中心的梯度惩罚的优越性的一般证明在《Which Training Methods for GANs do actually Converge?》中已经给出，并得到实验验证。

GAN-QP #

最后来分析一下自己提出的GAN-QP表现如何。相比WGAN-GP，GAN-QP用二次型的差分惩罚项替换了梯度惩罚，并补充了一些证明。相比梯度惩罚，差分惩罚的最主要优势是计算速度更快。

GAN-QP可以有多种形式，一种基本形式是：
\begin{equation}\begin{aligned}&\min_{D} \mathbb{E}_{\boldsymbol{x}_r\sim p(\boldsymbol{x}_r),\boldsymbol{x}_f\sim q(\boldsymbol{x}_f)}\left[D(\boldsymbol{x}_f) - D(\boldsymbol{x}_r) + \frac{(D(\boldsymbol{x}_f) - D(\boldsymbol{x}_r))^2}{2\lambda \Vert \boldsymbol{x}_f - \boldsymbol{x}_r\Vert}\right]\\
&\min_{G} \mathbb{E}_{\boldsymbol{z}\sim q(\boldsymbol{z})}[-D(G(\boldsymbol{z}))] \end{aligned}\end{equation}
对应的Dirac GAN为
\begin{equation}\begin{aligned}&\min_{\boldsymbol{\varphi}} \boldsymbol{\theta}\cdot\boldsymbol{\varphi} + \frac{(\boldsymbol{\theta}\cdot\boldsymbol{\varphi})^2}{2\lambda \Vert \boldsymbol{\theta}\Vert}\\
&\min_{\boldsymbol{\theta}} -\boldsymbol{\theta}\cdot\boldsymbol{\varphi}\end{aligned}\end{equation}
对应的动力系统是：
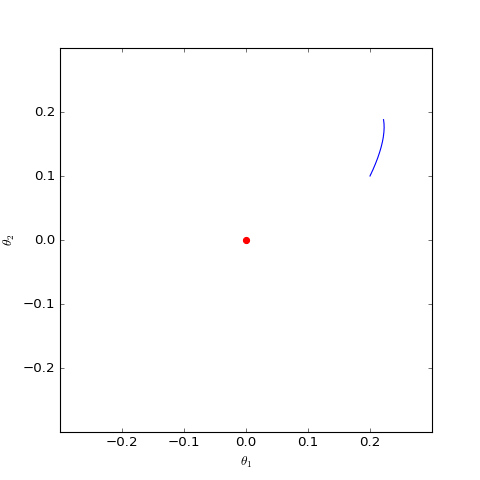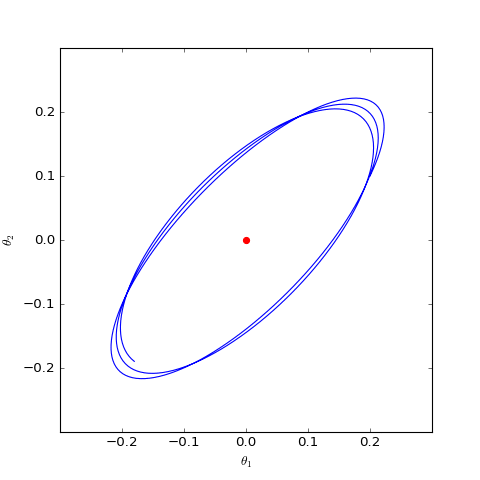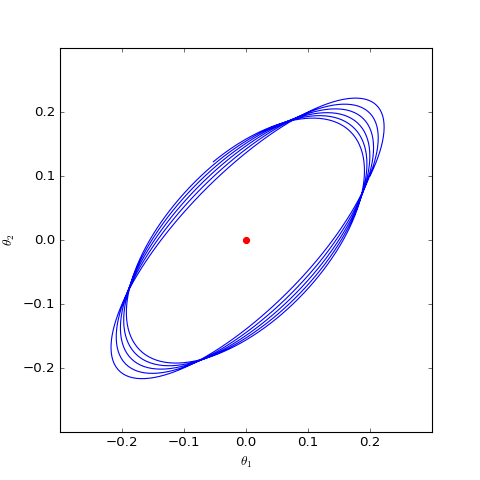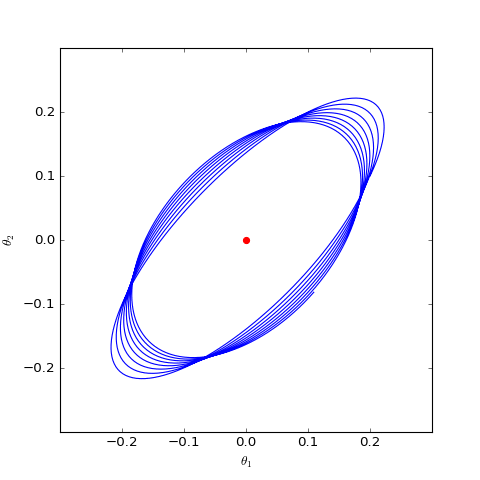
\begin{equation}\begin{pmatrix}\dot{\boldsymbol{\varphi}}\\ \dot{\boldsymbol{\theta}}\end{pmatrix} = \begin{pmatrix} \nabla_{\boldsymbol{\varphi}} (-\boldsymbol{\theta}\cdot\boldsymbol{\varphi} - (\boldsymbol{\theta}\cdot\boldsymbol{\varphi})^2 / (2\lambda \Vert \boldsymbol{\theta}\Vert))\\ \nabla_{\boldsymbol{\theta}} (\boldsymbol{\theta}\cdot\boldsymbol{\varphi})\end{pmatrix} = \begin{pmatrix} -\boldsymbol{\theta} - (\boldsymbol{\theta}\cdot\boldsymbol{\varphi})\boldsymbol{\theta}/(\lambda \Vert \boldsymbol{\theta}\Vert)\\ \boldsymbol{\varphi} \end{pmatrix}\end{equation}
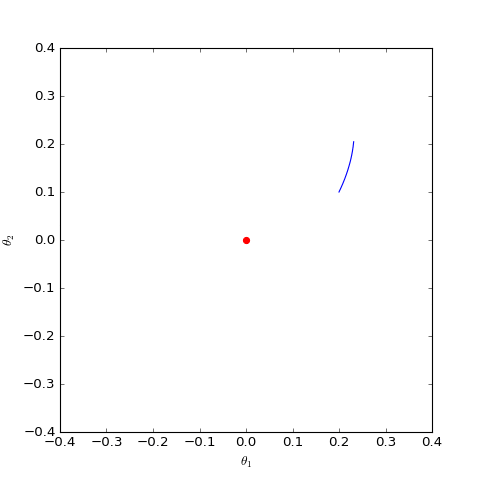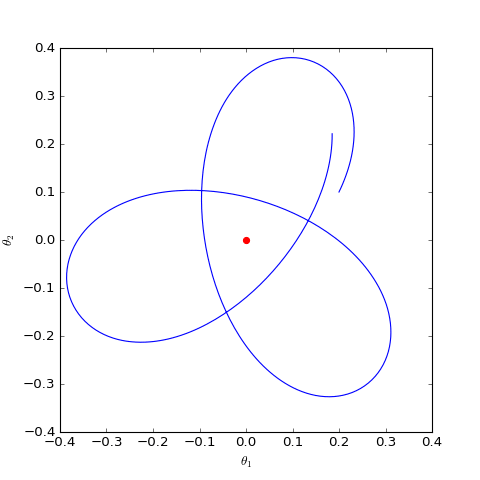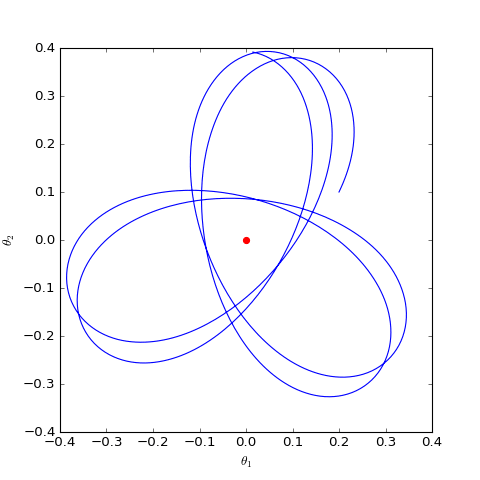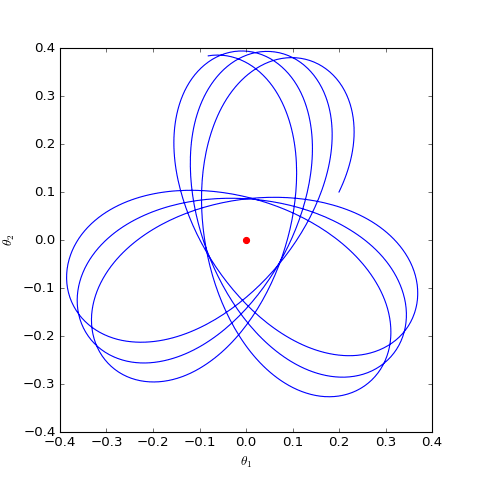
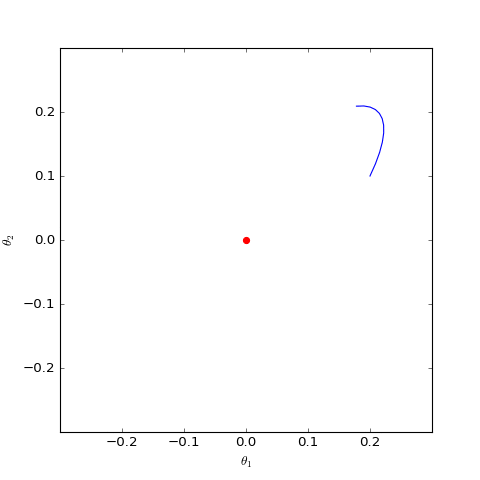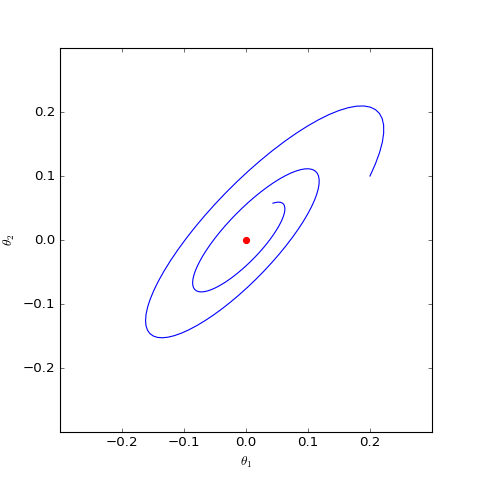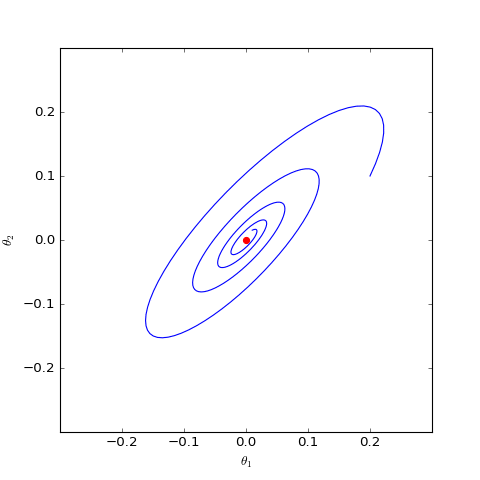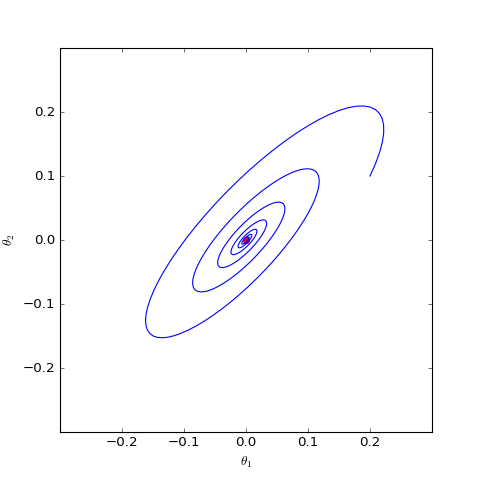
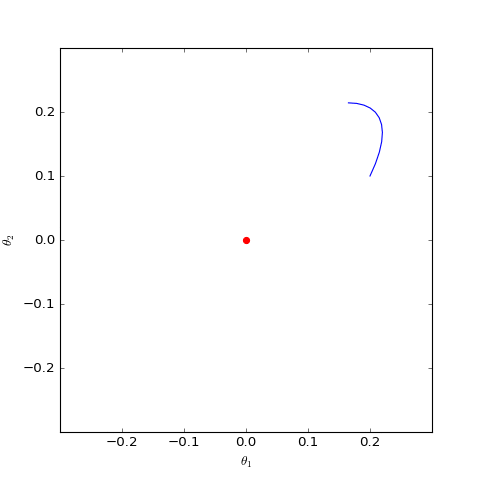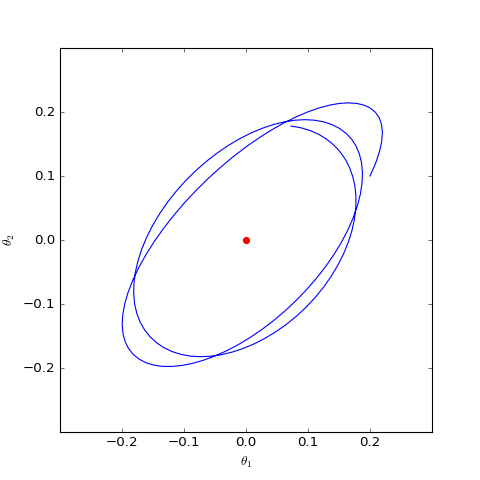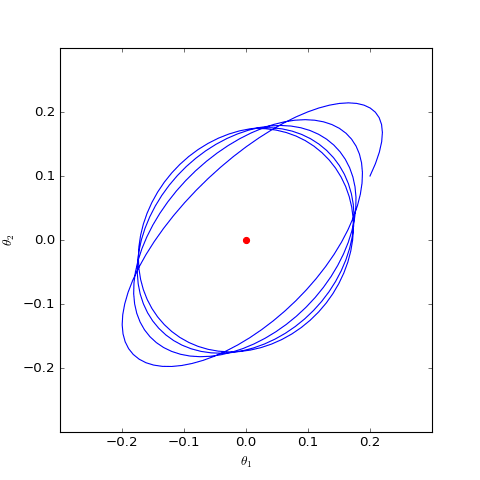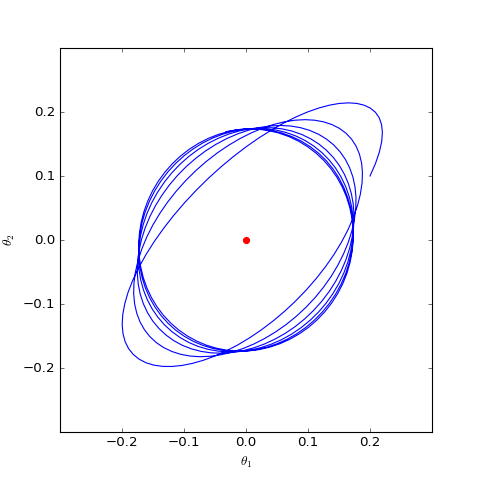
数值结果如下图（第一个图像）：

数值求解的GAN-QP对应的Dirac GAN的优化轨迹（二维情形），可以发现它确实只是在均衡点（红色点）周围振荡，不收敛

数值求解的GAN-QP对应的Dirac GAN的优化轨迹（二维情形），可以发现它确实只是在均衡点（红色点）周围振荡，不收敛

数值求解的带有L2正则项的GAN-QP版本的Dirac GAN，其他条件一样，仅加入了L2正则，这表明适当的L2正则项有可能诱导收敛

数值求解的带有L2正则项的GAN-QP版本的Dirac GAN，其他条件一样，仅加入了L2正则，这表明适当的L2正则项有可能诱导收敛

很遗憾，同大多数GAN一样，GAN-QP也是振荡的。

缓解策略 #

通过上面的分析，我们得到的结论是：目前零中心的WGAN-GP（或者称为WGAN-div）的理论性质最好，只有它是局部收敛的，其余的GAN变体都一定的振荡性，无法真正做到渐近收敛。当然，实际情况可能复杂得多，Dirac GAN的结论只能一定程度上说明问题，带来一个直观感知。

那么，如果Dirac GAN的结论具有代表性的话（即多数GAN实际情况下都难以真正收敛，而是在均衡点附近振荡），我们应该如何缓解这个问题呢？

L2正则项 #

第一个方案是考虑往（任意GAN的）判别器的权重加入L2正则项。综上所述，零中心的梯度惩罚确实很好，但无奈梯度惩罚太慢，如果不愿意加梯度惩罚，那么可以考虑加入L2正则项。

直观上看，GAN在均衡点附近陷入振荡，达到一种动态平衡（周期解，而不是静态解），而L2正则项会迫使判别器的权重向零移动，从而有可能打破这种平衡，如上图中的第二个图像。在我自己的GAN实验中，往判别器加入一个轻微的L2正则项，能使得模型收敛更稳定，效果也有轻微提升。（当然，正则项的权重需要根据模型来调整好。）

权重滑动平均 #

事实上，缓解这个问题最有力的技巧，当属权重滑动平均（EMA）。

权重滑动平均的基本概念，我们在《“让Keras更酷一些！”：中间变量、权重滑动和安全生成器》已经介绍过。对于GAN上的应用，其实不难理解，因为可以观察到，尽管多数GAN最终都是在振荡，但它们振荡中心就是均衡点！所以解决方法很简单，直接将振荡的轨迹上的点平均一下，得到近似的振荡中心，然后就得到了一个更接近均衡点（也就是更高质量）的解！

权重滑动平均带来的提升是非常可观的，如下图比较了有无权重滑动平均时，O-GAN的生成效果图：

没有权重滑动平均时的随机生成效果

没有权重滑动平均时的随机生成效果

权重滑动平均的衰减率为0.999时的随机生成效果

权重滑动平均的衰减率为0.999时的随机生成效果

权重滑动平均的衰减率为0.9999时的随机生成效果

权重滑动平均的衰减率为0.9999时的随机生成效果

可以看到，权重滑动平均几乎给生成效果带来了质的提升。衰减率越大，所得到的生成结果越平滑，但同时会丧失一些细节；衰减率越小，保留的细节越多，但自然也可能保留了额外的噪声。现在主流的GAN都使用了权重滑动平均，衰减率一般为0.999。

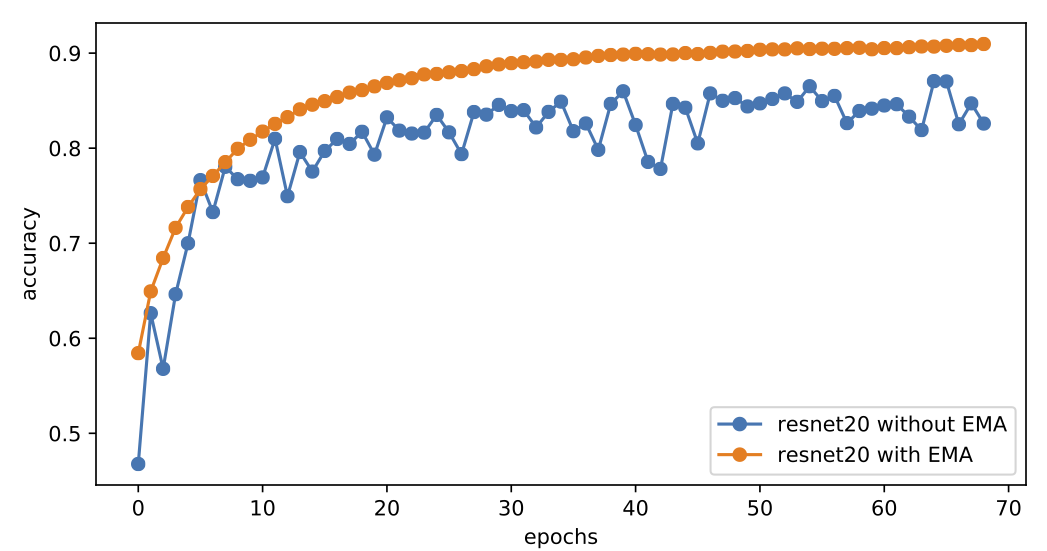
顺便说一下，在普通的监督训练模型中，权重滑动平均一般也能带来收敛速度的提升，比如下图是有/无权重滑动平均时，ResNet20模型在cifar10上的训练曲线，全程采用Adam优化器训练，学习率恒为0.001，权重滑动平均的衰减率为0.9999：

有无EMA时Adam默认学习率训练ResNet20的表现

有无EMA时Adam默认学习率训练ResNet20的表现

可以看到，加上权重滑动平均之后，模型以一种非常平稳、快速的姿态收敛到90%+的准确率，而不加的话模型准确率一直在86%左右振荡。这说明类似GAN的振荡现象在深度学习训练时是普遍存在的，通过权重平均可以得到质量更好的模型。

文章小结 #

本文主要从动力学角度探讨了GAN的优化问题。跟本系列的其他文章一样，将优化过程视为常微分方程组的求解，对于GAN的优化，这个常微分方程组稍微复杂一些。

分析的过程采用了Dirac GAN的思路，利用单点分布的极简情形对GAN的收敛过程形成快速认识，得到的结论是大多数GAN都无法真正收敛到均衡点，而只是在均衡点附近振荡。而为了缓解这个问题，最有力的方法是权重滑动平均，它对GAN和普通模型训练都有一定帮助。

（本文作图代码参考：https://github.com/bojone/gan/blob/master/gan_numeric.py）

转载到请包括本文地址：https://spaces.ac.cn/archives/6583

更详细的转载事宜请参考：《科学空间FAQ》

如果您还有什么疑惑或建议，欢迎在下方评论区继续讨论。

如果您觉得本文还不错，欢迎分享/打赏本文。打赏并非要从中获得收益，而是希望知道科学空间获得了多少读者的真心关注。当然，如果你无视它，也不会影响你的阅读。再次表示欢迎和感谢！

如果您需要引用本文，请参考：

苏剑林. (May. 03, 2019). 《从动力学角度看优化算法（四）：GAN的第三个阶段 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/6583

@online{kexuefm-6583,
        title={从动力学角度看优化算法（四）：GAN的第三个阶段},
        author={苏剑林},
        year={2019},
        month={May},
        url={\url{https://spaces.ac.cn/archives/6583}},
}