由于专业需求，需要做主方程的随机模拟。在网上并没有找到适合的Python实现，遂自己写了一个，分享一下源码。至于gillespie算法本身就不介绍了，有需要的读者自然会懂，没需要的读者不建议去懂。

源码 #

其实基本的gillespie模拟算法很简单，也很好实现，下面就是一个参考例子：

#! -*- coding: utf-8 -*-

import numpy as np
from scipy.special import comb


class Reaction: # 封装的类，代表每一个化学反应
    def __init__(self, rate=0., num_lefts=None, num_rights=None):
        self.rate = rate # 反应速率
        assert len(num_lefts) == len(num_rights)
        self.num_lefts = np.array(num_lefts) # 反应前各个反应物的数目
        self.num_rights = np.array(num_rights) # 反应后各个反应物的数目
        self.num_diff = self.num_rights - self.num_lefts # 改变数
    def combine(self, n, s): # 算组合数
        return np.prod(comb(n, s))
    def propensity(self, n): # 算反应倾向函数
        return self.rate * self.combine(n, self.num_lefts)


class System: # 封装的类，代表多个化学反应构成的系统
    def __init__(self, num_elements):
        assert num_elements > 0
        self.num_elements = num_elements # 系统内的反应物的类别数
        self.reactions = [] # 反应集合
    def add_reaction(self, rate=0., num_lefts=None, num_rights=None):
        assert len(num_lefts) == self.num_elements
        assert len(num_rights) == self.num_elements
        self.reactions.append(Reaction(rate, num_lefts, num_rights))
    def evolute(self, steps, inits=None): # 模拟演化
        self.t = [0] # 时间轨迹，t[0]是初始时间
        if inits is None:
            self.n = [np.ones(self.num_elements)]
        else:
            self.n = [np.array(inits)] # 反应物数目，n[0]是初始数目
        for i in range(steps):
            A = np.array([rec.propensity(self.n[-1])
                          for rec in self.reactions]) # 算每个反应的倾向函数
            A0 = A.sum()
            A /= A0 # 归一化得到概率分布
            t0 = -np.log(np.random.random())/A0 # 按概率选择下一个反应发生的间隔
            self.t.append(self.t[-1] + t0)
            d = np.random.choice(self.reactions, p=A) # 按概率选择其中一个反应发生
            self.n.append(self.n[-1] + d.num_diff)

使用 #

为了方便使用，我对反应进行了封装。现在，只需要根据反应式就可以直接进行模拟了，无须额外的编程操作。比如比较简单的基因表达模型：
$$\begin{aligned}DNA &\xrightarrow{\quad 20\quad} DNA + m\\
m &\xrightarrow{\quad 2.5\quad} m + n\\
m &\xrightarrow{\,\quad 1\,\,\quad} \phi\\
n &\xrightarrow{\,\quad 1\,\,\quad} \phi
\end{aligned}$$
这里$m,n$分别代表mRNA和蛋白质的数目，$\phi$是空，意味着降解或者“无中生有”。其中第一个反应可以简化为$\phi \xrightarrow{\quad 20\quad} m$，所以实际上是两种反应物$m,n$的四个反应式。

num_elements = 2
system = System(num_elements)

system.add_reaction(20, [0, 0], [1, 0])
system.add_reaction(2.5, [1, 0], [1, 1])
system.add_reaction(1, [1, 0], [0, 0])
system.add_reaction(1, [0, 1], [0, 0])

system.evolute(100000)

然后就可以统计画图：

import matplotlib.pyplot as plt
import pandas as pd

x = system.t
y = [i[1] for i in system.n]

plt.clf()
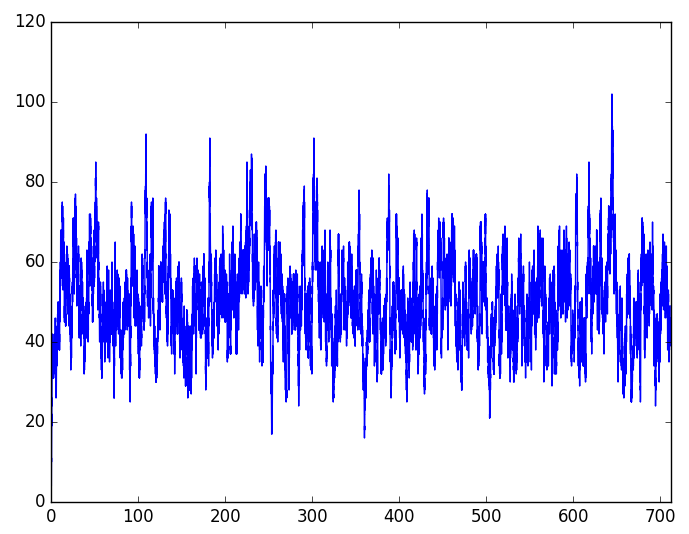
plt.plot(x, y) # 蛋白质的轨线图
plt.xlim(0, x[-1]+1)
plt.savefig('test.png')

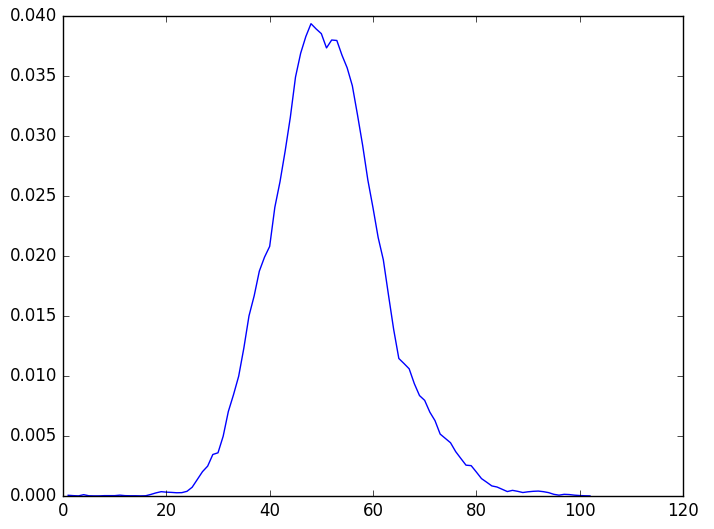
d = pd.Series([i[1] for i in system.n]).value_counts()
d = d.sort_index()
d /= d.sum()
plt.clf()
plt.plot(d.index, d) # 蛋白质的（经验）分布图
plt.savefig('test.png')

结果为：

蛋白质随时间的变化（轨线）

蛋白质随时间的变化（轨线）

蛋白质的统计分布

蛋白质的统计分布

转载到请包括本文地址：https://spaces.ac.cn/archives/5607

更详细的转载事宜请参考：《科学空间FAQ》

如果您还有什么疑惑或建议，欢迎在下方评论区继续讨论。

如果您觉得本文还不错，欢迎分享/打赏本文。打赏并非要从中获得收益，而是希望知道科学空间获得了多少读者的真心关注。当然，如果你无视它，也不会影响你的阅读。再次表示欢迎和感谢！

如果您需要引用本文，请参考：

苏剑林. (Jun. 07, 2018). 《python简单实现gillespie模拟 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/5607

@online{kexuefm-5607,
        title={python简单实现gillespie模拟},
        author={苏剑林},
        year={2018},
        month={Jun},
        url={\url{https://spaces.ac.cn/archives/5607}},
}