科学空间|Scientific Spaces

这一篇“让Keras更酷一些！”将和读者分享两部分内容：第一部分是“层中层”，顾名思义，是在Keras中自定义层的时候，重用已有的层，这将大大减少自定义层的代码量；另外一部分就是应读者所求，介绍一下序列模型中的mask原理和方法。

层中层

在《“让Keras更酷一些！”：精巧的层与花式的回调》一文中我们已经介绍过Keras自定义层的基本方法，其核心步骤是定义build和call两个函数，其中build负责创建可训练的权重，而call则定义具体的运算。

拒绝重复劳动

经常用到自定义层的读者可能会感觉到，在自定义层的时候我们经常在重复劳动，比如我们想要增加一个线性变换，那就要在build中增加一个kernel和bias变量（还要自定义变量的初始化、正则化等），然后在call里边用K.dot来执行，有时候还需要考虑维度对齐的问题，步骤比较繁琐。但事实上，一个线性变换其实就是一个不加激活函数的Dense层罢了，如果在自定义层时能重用已有的层，那显然就可以大大节省代码量了。

点击阅读全文...

前两周又在群里看到一个颇为有趣的问题：两个同样大小的椭圆片可以沿着它们的长轴弯曲，沿着边缘线粘贴，能完美地贴合成一个封闭立体吗？问题来源于知乎《两个椭圆片可否以柱面弯曲边缘完美贴合？》。

两个椭圆片粘合图示（截取自知乎上提问的图示）

问题可以用只言片语表达清楚，甚至普通读者都能理解，而问题本身是有一定难度的，这就符合了一个漂亮的问题的条件，所以也就吸引了笔者陆陆续续思考了好多天，最终在昨天算是给出了这类问题通用的列方程思路和数值求解方案，而今天则完成了理论证明，确认两个相同椭圆片总是可以完美贴合。

点击阅读全文...

最近用Keras实现了两个优化器，也算是有点实现技巧，遂放在一起写篇文章简介一下（如果只有一个的话我就不写了）。这两个优化器的名字都挺有意思的，一个是look ahead（往前看？），一个是lazy（偷懒？），难道是两个完全不同的优化思路么？非也非也～只能说发明者们起名字太有创意了。

Lookahead

首先登场的是Lookahead优化器，它源于论文《Lookahead Optimizer: k steps forward, 1 step back》，是最近才提出来的优化器，有意思的是大牛Hinton和Adam的作者之一Jimmy Ba也出现在了论文作者列表当中，有这两个大神加持，这个优化器的出现便吸引了不少目光。

点击阅读全文...

前几个月曾参加了百度的实体链接比赛，这是CCKS2019的评测任务之一，官方称之为“实体链指”，比赛于前几个星期完全结束。笔者最终的F1是0.78左右（冠军是0.80），排在第14名，成绩并不突出（唯一的特色是模型很轻量级，GTX1060都可以轻松跑起来），所以本文只是纯粹的记录过程，大牛们请一笑置之～

本文的实体链接模型总图（可以点击查看大图）

赛题介绍

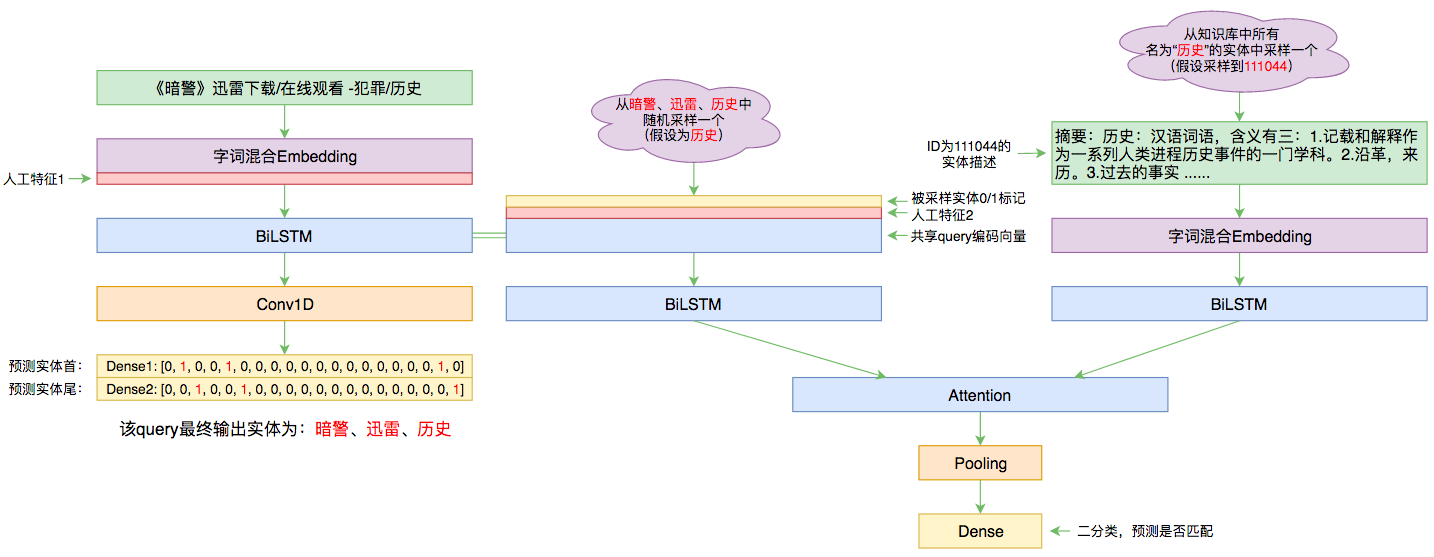
所谓实体链接，主要指的是在已有一个知识库的情况下，预测输入query的某个实体对应知识库id。也就是说，知识库里边记录了很多实体，对于同一个名字的实体可能会有多个解释，每个解释用一个唯一id编号，我们要做的就是预测query中的实体究竟对应哪一个解释（id）。这是基于知识图谱的问答系统的必要步骤。

点击阅读全文...

在我看来，几大顶会之中，ICLR的论文通常是最有意思的，因为它们的选题和风格基本上都比较轻松活泼、天马行空，让人有脑洞大开之感。所以，ICLR 2020的投稿论文列表出来之后，我也抽时间粗略过了一下这些论文，确实发现了不少有意思的工作。

其中，我发现了两篇利用去噪自编码器的思想做生成模型的论文，分别是《Learning Generative Models using Denoising Density Estimators》和《Annealed Denoising Score Matching: Learning Energy-Based Models in High-Dimensional Spaces》。由于常规做生成模型的思路我基本都有所了解，所以这种“别具一格”的思路就引起了我的兴趣。细读之下，发现两者的出发点是一致的，但是具体做法又有所不同，最终的落脚点又是一样的，颇有“一题多解”的美妙，遂将这两篇论文放在一起，对比分析一翻。

fashion mnist、CelebA、cifar10上的生成效果

点击阅读全文...

对于复杂模型来说，参数的初始化显得尤为重要。糟糕的初始化，很多时候已经不单是模型效果变差的问题了，还更有可能是模型根本训练不动或者不收敛。在深度学习中常见的自适应初始化策略是Xavier初始化，它是从正态分布$\mathcal{N}\left(0,\frac{2}{fan_{in} + fan_{out}}\right)$中随机采样而构成的初始权重，其中$fan_{in}$是输入的维度而$fan_{out}$是输出的维度。其他初始化策略基本上也类似，只不过假设有所不同，导致最终形式略有差别。

标准的初始化策略的推导是基于概率统计的，大概的思路是假设输入数据的均值为0、方差为1，然后期望输出数据也保持均值为0、方差为1，然后推导出初始变换应该满足的均值和方差条件。这个过程理论上没啥问题，但在笔者看来依然不够直观，而且推导过程的假设有点多。本文则希望能从几何视角来理解模型的初始化方法，给出一个更直观的推导过程。

信手拈来的正交

前者时间笔者写了《n维空间下两个随机向量的夹角分布》，其中的一个推论是

推论1： 高维空间中的任意两个随机向量几乎都是垂直的。

点击阅读全文...

HMM、MEMM、CRF被称为是三大经典概率图模型，在深度学习之前的机器学习时代，它们被广泛用于各种序列标注相关的任务中。一个有趣的现象是，到了深度学习时代，HMM和MEMM似乎都“没落”了，舞台上就只留下CRF。相信做NLP的读者朋友们就算没亲自做过也会听说过BiLSTM+CRF做中文分词、命名实体识别等任务，却几乎没有听说过BiLSTM+HMM、BiLSTM+MEMM的，这是为什么呢？

今天就让我们来学习一番MEMM，并且通过与CRF的对比，来让我们更深刻地理解概率图模型的思想与设计。

模型推导

MEMM全称Maximum Entropy Markov Model，中文名可译为“最大熵马尔可夫模型”。不得不说，这个名字可能会吓退80%的初学者：最大熵还没搞懂，马尔可夫也不认识，这两个合起来怕不是天书？而事实上，不管是MEMM还是CRF，它们的模型都远比它们的名字来得简单，它们的概念和设计都非常朴素自然，并不难理解。

点击阅读全文...

当前，说到深度学习中的对抗，一般会有两个含义：一个是生成对抗网络（Generative Adversarial Networks，GAN），代表着一大类先进的生成模型；另一个则是跟对抗攻击、对抗样本相关的领域，它跟GAN相关，但又很不一样，它主要关心的是模型在小扰动下的稳健性。本博客里以前所涉及的对抗话题，都是前一种含义，而今天，我们来聊聊后一种含义中的“对抗训练”。

本文包括如下内容：

1、对抗样本、对抗训练等基本概念的介绍；

2、介绍基于快速梯度上升的对抗训练及其在NLP中的应用；

3、给出了对抗训练的Keras实现（一行代码调用）；

4、讨论了对抗训练与梯度惩罚的等价性；

5、基于梯度惩罚，给出了一种对抗训练的直观的几何理解。

点击阅读全文...