科学空间|Scientific Spaces

之前在这篇文章中，我们使用过一个牛顿引力场中的自由落体公式：
$t=\sqrt{\frac{r_0}{2GM}}{r_0 \cdot arctg \sqrt{\frac{r_0 -r}{r}}+\sqrt{r(r_0 -r)}}$——（1）

我们来尝试一下推导出这个公式来。同时，站长在逐渐深入研究的过程中，发现微分方程极其重要。以前一些我认为不可能解决的问题，都用微分方程逐渐解决了。在以后的文章里，我们将会继续体验到微分方程的伟大魔力！因此，建议各位有志研究物理学的朋友，一定要掌握微分方程，更加深入的，需要用到偏微分方程！

首先，质量为m的物理在距离地心r处的引力为$\frac{GMm}{r^2}$，根据牛顿第二定律F=ma，自然下落的物体所获得的加速度为$\frac{GM}{r^2}$。假设物体从距离地心r开始向地心自由下落，求位移s关于t的函数s=s(t).

点击阅读全文...

在初中或高中，自由落体试验简单地用这个公式来描述出来：
$$s=1/2 g t^2$$
其中$g=9.8m//s^2$，等于1kg物体在地球表面所受的重力。
但是这个公式很明显有一个问题，就是实际上在地球，g不是恒定的，会随着距离（即海拔高度）的变化而变化，上述公式能够在一定范围内描述自然落体运动。但是当距离很大时，公式便失效了。

点击阅读全文...

自由落体公式-示意图

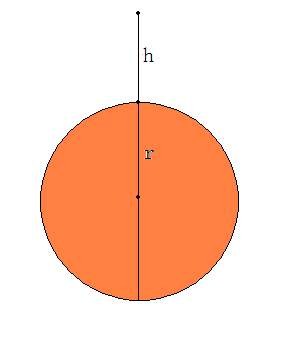
自由落体的一般定义是：只考虑吸引天体和被吸引天体的引力因素，忽略其他的运动和大气摩擦等因素，物体从静止（相对于吸引天体）开始接近吸引天体的运动。根据这个定义，假设地球为一个均匀球体，半径为r，质量为M，物体从距离地表h高度处自由落下。求落到地面的时间t，或者根据时间t求h。

令s为t时刻物体左右下落的物体与地表的距离，忽略物体的小质量，那么可以列出微分方程：
$$\frac{d^2 s}{dt^2}=-\frac{GM}{(r+s)^2}\tag{1}$$并且初始条件是$t=0,s=h,\dot{s}=v=0$

在实际应用中，我们不必求出这道微分方程的精确解，因为这个解极其麻烦，在之前曾经讨论过。我们只需要求出一个有足够精确度的近似解就行。

点击阅读全文...

草蜢

保护色（Crypsis）和拟态现象都表现为与环境色彩相似，不易被识别，保护色表现为与环境色彩相似，这里的“环境色彩”应是环境中主要的占优势的色彩，如春夏的草坪是绿色，冬天的雪地是白色；拟态是与环境中某种生物或非生物相似，而这种生物或非生物的颜色等特征并不一定在环境中占优势，并非主要色彩，保护色则与运动状态基本无关，如枯叶蝶停息在树枝上的模样像枯叶，“停息”状态才像枯叶，一旦飞舞起来就不像了。而我们捕捉昆虫也许都有这种体验：有时看到昆虫由这里飞向另一个地方，但马上在另一个地方搜寻，却不能立即找到。

点击阅读全文...

附：期中考过后，课程紧了，自由时间少了，因此科学空间的更新也放缓了。不过BoJone也会尽量地更新一些内容，和大家一同分享学习的乐趣。

闭区间[a,b]上的连续函数?(x)，其最大值为红色点，最小值为蓝色点

上一周和这一周的时间里，BoJone将自己学习物理和极值的一些内容进行了总结和整合，写成了《自然极值》一文。因此从今天起，到十二月的大多数时间里，科学空间将和大家讲述并讨论关于“极值”的问题，希望读者会喜欢这部分内容。当然，我不是专业的研究人员，更不是经验丰富的物理和数学教师，甚至可以说是一个“乳臭未干的小子”，因此，错误在所难免，只希望同好不吝指出，更希冀能够起到我抛出的这一块“砖”能够引出美妙的“玉”。

点击阅读全文...

物理学的美不仅仅表现在简洁的公式上。我们还惊奇地发现，很多物理现象都是按照使某个变量达到极值的方式发生。一个典型的例子就是费马原理，它指出了光的传播路径的一个重要规律：光总是沿着所花时间最短的路径传播。这里我们将简单介绍一下费马原理。

费马原理俗称“最快到达原理”、“最小时间原理”。1657年，费马提出：

从P点到达Q点，在所有可行的路径中，光选择了所需时间最短的一条。

从P点到达Q点，在所有可行的路径中，光选择了所需时间为极值的一条。

这是一个极其奇妙的原理，也是自然界中最神奇的极值之一。作为非生物的光，居然自主地选择了最优路径，成为世界上“效率最高”的东西，这让人不得不佩服宇宙的伟大。这究竟是造物者的精心设计，还是无心之作？

点击阅读全文...

黄果树大瀑布

光学定律无疑是一个美妙的原理，而自然界中还存在另外一个我们随处可见的“公理”。平时的生活中，我们总能看见“水往低处流”的现象，这是因为水处于地球重力场的结果（也正因为如此，某些轻生者的自杀活动才得以顺利进行；当然，我们并不需要为了验证这一点而亲自试验。）。由此我们可以联想到一个名词：重力势能。“水往低处流”意味着什么呢？高度变低了。高度更低意味着什么呢？重力势能降低了！换句话说，自然界中物体有趋于势能最低的倾向。我们可以从这个角度来解释：体系总有趋于稳定的倾向，而拥有的能量（势能）越高，则越不稳定。

点击阅读全文...

如果说前面关于这个系列的内容还不能使得读者您感到痛快，那么接下来要讲述的最速降线和悬链线问题也许能够满足你的需要。不过在进入对最速降线问题的理论探讨之前，我们先来讲述一个发生在17世纪的激动人心的数学竞赛的故事。我相信，每一个热爱数学和物理的朋友，都将会为其所振奋，为其所感动。里边渗透的，不仅仅是一次学术的竞争，更是一代又一代的人对真理的追求与探路的不懈精神。

（以下内容来源于网络，科学空间整理）

意大利科学家伽利略在1630年提出一个分析学的基本问题── “一个质点在重力作用下，从一个给定点A到不在它垂直下方的另一点B，如果不计摩擦力，问沿着什么曲线滑下所需时间最短。”这算是这个著名问题的起源了（为什么别人没有想起这个问题呢？所以说大科学家的素质就是思考、创新，要有思想，人没有思想，就和行尸走肉没有什么区别）。可惜的是伽利略说这曲线是圆，但这却是一个错误的答案。

Brachistochrone

点击阅读全文...