流体静力平衡的应用

很早以前我就对这个问题感兴趣了，但是一直搁置着，没有怎么研究。最近在阅读《引力与时空》的“潮汐力”那一节时重新回到了这个问题上，决定写点什么东西。在这里不深究流体静力平衡的定义，顾名思义地理解，它就是流体在某个特定的力场下所达到的平衡状态。流体静力学告诉我们：

达到流体静力平衡时，流体的面必定是一个等势面。

这是为什么呢？我们从数学的角度来简单分析一下：只考虑二维情况，假如等势面方程是$U(x,y)=C$，那么两边微分就有
$$0=dU=\frac{\partial U}{\partial x}dx+\frac{\partial U}{\partial y}dy=(\frac{\partial U}{\partial x},\frac{\partial U}{\partial y})\cdot (dx,dy)$$

这意味着向量$(\frac{\partial U}{\partial x},\frac{\partial U}{\partial y})$和向量$(dx,dy)$是垂直的，前者便是力的函数，后者就是一个切向量（三维就是一个切平面）。也就是说合外力必然和流体面垂直，这样才能提供一个相等的方向相反的内力让整个结构体系处于平衡状态！

这个结果在天文中还是有相当多的应用的，下面仅举两例：

一、地球扁率问题

这个问题之前我们已经探讨过了，但是之前的探究仅仅是基于一个不一定成立的假设，可以说是没有物理基础的。现在我们从流体静力学平衡角度给出一个推导。

等等，有的读者会叫板了，地球明明是一个固体星球，怎么又扯上流体了？这里流体平衡状态实际上是物体分布的一种问题状态。不错，地球确实是固体（刚体），不像空气和液体那样容易达到平衡。但是地球已经形成了40多亿年了，据研究地球自转速度在不断变慢中，也就是说今天的自转速度几乎可以说是有史以来的一个下限了。在长期的运动中，微小的离心力不断作用之下，地球形状也会趋于一个流体静力平衡状态。用来估算扁率的大小，也是符合实际的。

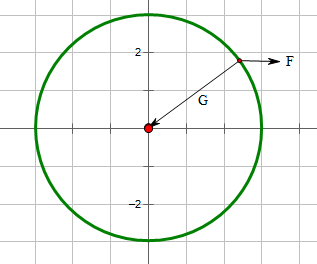
简单分析，地球表面的一个小物体受到两个力的作用，一是地球引力，二是地球自转所带来的“离心力”，如图：

地球表面引力可以记为$mg$，引力势能为$mgh=mg(r-R)$，R是地球的极半径；离心力为$F=m\omega^2 x$，所以离心势能为$-\frac{1}{2}m\omega^2 x^2$。这样的一个等势面就是：
$$gh-\frac{1}{2}\omega^2 x^2=C$$

当x=0（北极点或者南极点）时，h=0，于是$C=0$。于是地球形状方程为
$$g(r-R)-\frac{1}{2}\omega^2 x^2=0$$

在赤道，有
$$gh=\frac{1}{2}\omega^2 (R+h)^2 \approx \frac{1}{2}\omega^2 (R^2+2Rh)$$

解得
$$h=\frac{\omega^2 R^2}{2(g-\omega^2 R)}$$

因为$\omega^2 R$是小量，直接无视它，就得到扁率为
$$\frac{h}{R}=\frac{\omega^2 R}{2g}$$

这其实就是我们在之前的文章得到的结果的一半。也许有的读者会疑问，之前得到的结果不是已经符合得很好了吗？现在取一半，偏差不是更大？的确偏离大了，但是这是基于物理定律推导出来的结果，在理论上有说服力。至于偏离较大的问题，则是由于我们的理想化模型而致，影响地球扁率的还有很多很多......

二、潮汐

同样的模型我们还可以用来估算地球的浪高，这是由于月球和太阳给我们带来的潮汐力所造成的，而月球则是主要的来源，其大小大约为太阳的两倍。潮汐力的大小是$\frac{2GMm}{d^3}x$，M是月球质量，d是地月距离，x简单理解就是地球上某点所在的纬圈半径，那么由潮汐力给我们带来的潮汐势能为$-\frac{GMm}{d^3}x^2$，地球的引力势能是$mgh$。要注意，海水与潮汐力的作用并没有达到流体静力平衡，但是由于海水易于变形，在受到潮汐力的作用时，它虽然不会固定在某个位置上，但是会在平衡位置徘徊，因此用流体静力平衡的位置来估计浪高是合理的。

于是流体静力平衡告诉我们：
$$gh-\frac{GM}{d^3}x^2=C$$

同样在两极应该有h=0，x=0，所以C=0，在赤道的话有：
$$gh=\frac{GM}{d^3}x^2 \approx \frac{GM}{d^3}R^2$$
即$h=\frac{GMR^2}{gd^3}\approx 0.37m$

这给出了37cm的浪高。这样看来估算还是合理的。当然地球上有比这远远高得多的浪，这是由各种不同的因素综合作用而成的。对于月球引力来说，这基本上就是它提供的贡献了。在农历初一的时候，月球、太阳的潮汐力叠加起来，上述计算将给出大约50cm的浪高，古时称之为“大潮”，在下弦（农历二十二左右），两者潮汐力相互抵消了一部分，引潮作用达到最低，称为“小潮”。当然，这仅仅是理论上的估计，只具有长期平均效应的意义。

转载到请包括本文地址：https://spaces.ac.cn/archives/1964

更详细的转载事宜请参考：《科学空间FAQ》