科学空间|Scientific Spaces

为了让大家更加熟悉摄动法的基本步骤，本文再讲一个用摄动法解代数方程的例子。这是从实际研究中出来的：
$$\begin{eqnarray*} x=\frac{k(1+k^2+k^4+l^2)}{2(1+k^2)^2} \\ k=\frac{dy}{dx}\end{eqnarray*} $$

这是一道微分方程。要求解这道方程，最好的方法当然是先从第一式解出$k=k(x)$的形式然后再积分。但是由于五次方程没有一般的显式解，所以迫使我们要考虑近似解。当然，一般来说熟悉mathematica的人都会直接数值计算了。我这里只考虑摄动法。

我们将原方程变为下面的形式：
$$x=\frac{k}{2}[1+\frac{l^2}{(1+k^2)^2}]$$

点击阅读全文...

刚刚在浏览卢昌海大师的微博时，发现他微博上有一道比较有趣的题目，于是饶有兴致地思考了一翻，构思了一个答案，希望读者们看看这个答案有问题不？

五一”长假微博很闷，出一道题给博友们解闷：

用重载列车运煤，每次可装1万吨，每行驶1公里耗煤1吨，起点处共有N万吨煤（简单起见N为正整数），请问最远可运至何处（是国营煤老板，成本不计，只要运到的数量大于0就算成功）？并求$N\to\infty$时的渐进形式。

点击阅读全文...

呵呵，做了一回标题党，可能说得夸张了一点。说是“终极算法”，主要是因为它可以任意提高精度、而且几乎可以应付任何非线性方程（至少理论上是这样），提高精度是已知的迭代式上添加一些项，而不是完全改变迭代式的形式，当然在提高精度的同时，计算量也会随之增大。其理论基础依旧是泰勒级数。

我们考虑方程$x=f(y)$，已知y求x是很容易的，但是已知x求y并不容易。我们考虑把y在$(x_0,y_0)$处展开成x的的泰勒级数。关键是求出y的n阶导数$\frac{d^n y}{dx^n}$。我们记$f^{(n)}(y)=\frac{d^n x}{dy^n}$，并且有
$$\frac{dy}{dx}=\frac{1}{(\frac{dx}{dy})}=f'(y)^{-1}$$

点击阅读全文...

当二次型在二维平面的情况下时，就等价于二次曲线的化简。二次曲线的化简主要用到平移和旋转，这恰好是复数所“擅长”的。因此，以复数为工具来对二次曲线进行化简，似乎是一种很显然的思路。然而，我却没有看到这方面的内容，而且我自己之前也忽略了这一思路。下面我对这个思路进行一点探索。

由于只打算做一些启发性引导，所以在这里只考虑$ Ax^2+2Bxy+Cy^2=1$这种不完全的形式（它不包含抛物线）。

点击阅读全文...

Ramanujan

在正式开始数学之前，我们不妨先说一个关于印度著名数学天才——拉马努金的轶事。拉马努金病重，哈代前往探望。哈代说：“我乘出租车来，车牌号码是1729，这数真没趣，希望不是不祥之兆。”拉马努金答道：“不，那是个有趣得很的数。可以用两个立方之和来表达而且有两种表达方式的数之中，1729是最小的。”（即$1729 = 1^3+12^3 = 9^3+10^3$，后来这类数称为的士数。）利特尔伍德回应这宗轶闻说：“每个整数都是拉马努金的朋友。”（来自维基百科）

从这则轶事中，我们发现，确实存在的某些整数，可以表示为两种不同的立方和，换句话说，不定方程：
$$x^3+y^3=z^3+w^3$$

点击阅读全文...

今天上近世代数课，老师谈到除环，举了一个非交换的除环的粒子，也就是四元数环，然后谈到“实数域上有限维可除代数只有4种”，也就是实数本身、复数、四元数和八元数（这里的可除代数就是除环）。这句话我听起来有点熟悉，又好像不大对劲。我记得在某本书上看过，定义为实数上的超复数系，如果满足模的积性，那么就只有以上四种。但是老师的那句话表明即使去掉模的积性，也只有四种。我自然以为老师记错了，跟老师辩论了一翻，然后回到宿舍又找资料，最终确定：实数域上有限维可除代数真的只有四种！下面简单谈谈我对这个问题的认识。

当然，这里不可能给出这个命题的证明，因为这个证明相当不简单，笔者目前也没有弄懂，但是粗略感觉一下为什么，还是有可能的。看到这个命题，我们一下子的感觉可能是：怎么会这么少！我们这里通过例子简单说明一下，确实不会多！

我们已经对复数系很熟悉了，也就是定义在实数上的向量空间，基为$\{1,i\}$，并且给定乘法为
$$1\times i=i \times 1=i,\quad 1^2=1,\quad i^2=-1$$

点击阅读全文...

魏尔斯特拉斯定理

将狄拉克函数理解为函数的极限，可以衍生出很丰富的内容，而且这些内容离严格的证明并不遥远。比如，定义
$$\delta_n(x)=\left\{\begin{aligned}&\frac{(1-x^2)^n}{I_n},x\in[-1,1]\\
&0,\text{其它情形}\end{aligned}\right.$$
其中$I_n = \int_{-1}^1 (1-x^2)^n dx$，于是不难证明
$$\delta(x)=\lim_{n\to\infty}\delta_n(x)$$
这样，对于$[a,b]$上的连续函数$f(x)$，我们就得到
$$f(x)=\int_{-1}^1 f(y)\delta(x-y)dy = \lim_{n\to\infty}\int_{-1}^1 f(y)\delta_n(x-y) dy$$
这里$-1 < a < b < 1$，并且我们已经“不严谨”地交换了积分号和极限号，但这不是特别重要。重要的是它的结果：可以看到
$$P_n(x)=\int_{-1}^1 f(y)\delta_n(x-y) dy$$
是$x$的一个$2n$次多项式，因此上式表明$f(x)$是一个$2n$次的多项式的极限！这就引出了著名的“魏尔斯特拉斯定理”：

闭区间上的连续函数都可以用多项式一致地逼近。

点击阅读全文...

从文章《从语言模型到Seq2Seq：Transformer如戏，全靠Mask》中我们可以知道，只要配合适当的Attention Mask，Bert（或者其他Transformer模型）就可以用来做无条件生成（Language Model）和序列翻译（Seq2Seq）任务。

可如果是有条件生成呢？比如控制文本的类别，按类别随机生成文本，也就是Conditional Language Model；又比如传入一副图像，来生成一段相关的文本描述，也就是Image Caption。

相关工作

八月份的论文《Encoder-Agnostic Adaptation for Conditional Language Generation》比较系统地分析了利用预训练模型做条件生成的几种方案；九月份有一篇论文《CTRL: A Conditional Transformer Language Model for Controllable Generation》提供了一个基于条件生成来预训练的模型，不过这本质还是跟GPT一样的语言模型，只能以文字输入为条件；而最近的论文《Plug and Play Language Models: a Simple Approach to Controlled Text Generation》将$p(x|y)$转化为$p(x)p(y|x)$来探究基于预训练模型的条件生成。

条件Normalization示意图

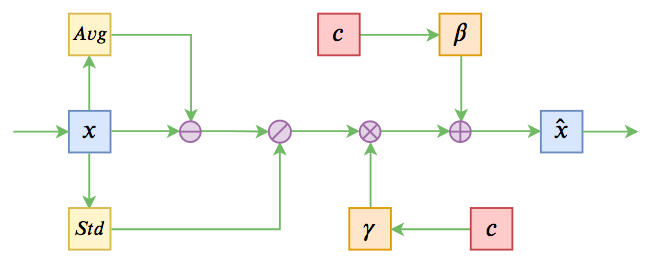
不过这些经典工作都不是本文要介绍的。本文关注的是以一个固定长度的向量作为条件的文本生成的场景，而方法是Conditional Layer Normalization——把条件融合到Layer Normalization的$\beta$和$\gamma$中去。

点击阅读全文...