科学空间|Scientific Spaces

在狭义相对论发表之前和之后，都有不少实验从不同角度论证了它的正确性。这些实验大多数是实际测量得出结果的，当然也存在着一些“理想实验”，这些实验只需要一定的逻辑推理，而实际上是无法完成的。下面就是我很久之前在某本书（很抱歉，我真的忘记书名了）看到的一个用来推翻光速可叠加的伽利略变换的理想实验。它只用寥寥几句，就好像已经证明了“c+c=c”（c是真空中的光速）的事实。可是“c+c=c”在狭义相对论上是作为原理出现的，是不可能通过逻辑推理来证明的。事实究竟如何？我们先来看这个实验。

光速不变的理想实验

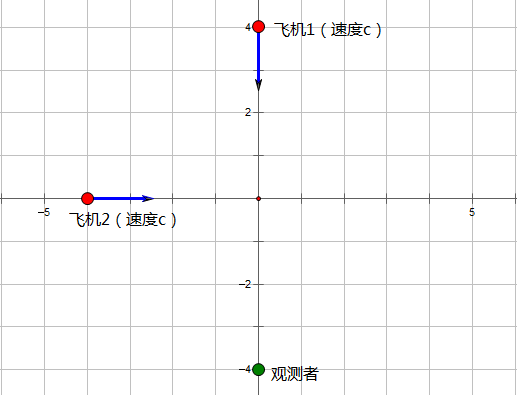
任意选定一个坐标原点。设想原点的正北方$c\cdot t_0$处有一架以光速$c$朝南运行的飞机1；原点的正西方$c\cdot t_0$处有一架以光速$c$朝东运行的飞机2。假设就这样匀速运动着，显然，$t_0$时间后，将会发生惨剧（飞机相撞）。

点击阅读全文...

在网上收集到的一些GIF，解释了不少机器构造的原理，其中有一些甚是巧妙！比如下面的椭圆规：

07椭圆规

也许以后学习或者科普的时候会用到，所以我将其打包为zip，收藏在这里，并与大家分享。里面包括一些武器和发动机的构造图，还有一些巧妙的部件，一些图片我已经注明该构造的名称，没有注明的是很显然的或者是找不到名称的。

点击阅读全文...

在天文爱好者眼中，黑洞是一个球体，其半径为$\frac{2GM}{c^2}$；这是广义相对论的施瓦兹黑洞的结果，也从经典力学推导推导出来，虽然用经典力学是错误的，但是对于多数的天文爱好者（包括笔者）来说，这是目前唯一的一种可行的理解方法（广义相对论那些复杂推导会让我们很崩溃的）。当然，事实上，黑洞不是一个球体，它只是一个密度很大的点。至于密度有多大，目前公认的说法是无穷大，但是严格的物理是不接受这个说法的，或者说，物理是不会接受任何无穷大的说法，所以现在积极发展量子引力理论来统一相对论和量子力学，不过这是另话了。$\frac{2GM}{c^2}$只不过是黑洞的视界，视界之内，我们就什么也不知道了。本文主要就从经典力学的角度探讨一下两个黑洞的合并过程中其视界的变化。读者将会发现，这些视界的形状相当有趣。

经典力学中的黑洞是这样定义的：天体表面的逃逸速度超过了光速，于是连光都无法逃脱，所以这个“洞”就很黑。也就是说，光子的总能量（引力势能与动能之和，经典力学意义下的）要为负，负数表示受到束缚。用数学公式来讲，就是：

$$\frac{1}{2}mc^2 - \frac{GM_1 m}{r_1}-\frac{GM_2 m}{r_2}-...-\frac{GM_n m}{r_n} \leq 0$$

点击阅读全文...

3、费曼图和量子电动力学的重整化

在1947年美国避难岛（Shelter Island)会议上，兰姆报导了他的重大发现，即现今所称的兰姆位移;氢原子的$2S_{\frac{1}{2}}$能级比$2P_{\frac{1}{2}}$高出约1000MHz。而按照狄拉克理论，对纯库仑相互作用的电子-质子系统，这两个能级应该是简并的。人们很快就认识到，该位移应归之于一阶近似的辐射校正[19]。贝特用一个电子的校正质量就非相对论近似得出了氢原子nS能级的位移公：

$$\frac{8}{3\pi}(\frac{e^2}{\hbar c})Ry \frac{Z^4}{n^3} Ln\frac{K}{ < E_n-E_m > _{AV}}$$

点击阅读全文...

一直都挺奇怪为什么这些天Blog都没有人来评论，难道我的文章质量下降了？可是统计显示访问人数比以往有所增加呀。一直郁闷但却无从找到答案。

今天收到了4anpan读者的邮件，表示评论解锁功能失效了。我自己测试才发现真的如此！！原来不一定是没有人来评论，而是评论插件出了问题。经排除，是最新的公式插件（ASCIIMathMLwFallback2）与滑动解锁的评论插件（IQapTcha）有冲突。所以只好把评论插件换回旧的验证码插件了。正在构思新一步的插件方案。

万分感谢4anpan读者的反馈，希望有更多的读者来帮忙完善科学空间。这里有你更精彩！！

期待你的声音^_^

大概在半年前，我曾用“化圆法”解决了椭圆内定长弦中点轨迹问题，求出了轨迹方程。前几天，我收到了网名为“理想”的网友的Email，他提出了自己对这个问题的解法，并得到了形式不同的轨迹方程，因此对两者的等价性表示疑惑。经过检验，我跟他的轨迹方程基本上是等价的，不过，他求出的轨迹方程总包括了原点，这是一点不足之处。但是看起来，他的轨迹方程却感觉好看一些。这的确很让人意外，因为从他的化简过程来看，有种“化简为繁”的味道，却得出了相当简洁的答案，着实有趣。

经过网友的同意，将他的过程贴在这里与大家分享！后面附有pdf文档，欢迎下载阅读。希望在科学空间可以看到更多的读者留下的痕迹。

椭圆定长弦中点轨迹的一种解法

作者：理想

本文介绍了一种计算椭圆定长弦中点轨迹的方法。设椭圆长、短轴分别为$2a$、$2b$，弦长为$2r$，随着弦的两端在椭圆上滑动，弦的中点形成的轨迹为：
$$(\frac{x^2}{a^2} + \frac{y^2}{b^2} - 1)(\frac{x^2}{a^4} + \frac{y^2}{b^4} + \frac{r^2}{a^2b^2}) + \frac{r^2}{a^2b^2} = 0$$
它不是一个椭圆，而是一个高次曲线。

点击阅读全文...

昨天晚上一位网友与我讨论以下问题：

函数$y=\sqrt{3} x-\frac{1}{x}$的图像为双曲线，在此双曲线的两支上分别取P、Q点，求PQ的最短距离。

显然，如果双曲线是普通的$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的形式，则这个问题是相当简单的。就是当y=0时两个点的距离，也就是2a。但是很明显这样的一条双曲线是经过旋转的。因此我们需要知道它究竟旋转了多少度$\theta$。然后列出$y=(\tan\theta) x$，联立双曲线方程就可以求出两个点了。

点击阅读全文...

今天早上子瑞给我发了一个问题来，他说：

一个数，各个数字加起来等于104，乘以2后各个数字加起来等于100，已知这个数字没有9，有4个8、3个7和2个6，问这个数字有多少个5？

当然这道题目不难，稍加分析就可以得出答案，不过不得不说这是一道趣题，而且更像一个数字游戏。

点击阅读全文...