4 Feb

[问题解答]双曲线上的最短距离

By 苏剑林 | 2013-02-04 | 28677位读者 |

昨天晚上一位网友与我讨论以下问题：

函数 $y=\sqrt{3} x-\frac{1}{x}$ 的图像为双曲线，在此双曲线的两支上分别取P、Q点，求PQ的最短距离。

显然，如果双曲线是普通的 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ 的形式，则这个问题是相当简单的。就是当y=0时两个点的距离，也就是2a。但是很明显这样的一条双曲线是经过旋转的。因此我们需要知道它究竟旋转了多少度 $\theta$ 。然后列出 $y=(\tan\theta) x$ ，联立双曲线方程就可以求出两个点了。

要求出旋转的角度，我们需要借助双曲线的两条渐近线。直线的问题总比双曲线问题容易处理一些。“渐近”就意味着当函数取极限的时候的大概形状。当 $x\to \infty$ 时， $\frac{1}{x} \to 0$ ，即其中一条渐近线为 $y=\sqrt{3} x$ ；另外，当 $x\to 0$ 时， $y\to \infty$ ，这说明另外一条渐近线为 $x=0$ ，后面一条渐近线的情况不妨类比 $y=\frac{1}{x}$ 的渐近线。

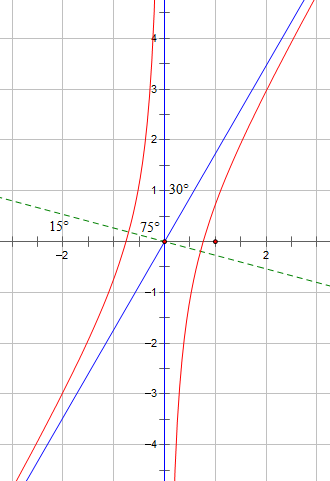
我们把双曲线和渐近线作图如下：

双曲线-渐近线

接下来只需要求出两条渐近线的角平分线方程即可，即图中的绿色虚线。经过简单的推理就可以得出绿色的虚线与x轴的负方向夹角为15°，即 $\frac{\pi}{12}$ ，通过：

$\frac{2 \tan\frac{\pi}{12}}{1-\tan^2 \frac{\pi}{12}}=\tan\frac{\pi}{6}=\frac{\sqrt{3}}{3}$

可以求出 $tan\frac{\pi}{12}=2-\sqrt{3}$ ，因此绿色虚线的方程为

$y=(\sqrt{3}-2)x$

联立 $y=\sqrt{3} x-\frac{1}{x}$ 可以求出

$x=\pm \frac{\sqrt{2}}{2}$
对应：

$y=\pm (\frac{\sqrt{6}}{2}-\sqrt{2})$

所以距离为

$\begin{aligned}2\sqrt{(\frac{\sqrt{6}}{2}-\sqrt{2})^2+(\frac{\sqrt{2}}{2})} \\ =2\sqrt{4-2\sqrt{3}} \\ =2(\sqrt{3}-1)\end{aligned}$

转载到请包括本文地址：https://spaces.ac.cn/archives/1904

更详细的转载事宜请参考：《科学空间FAQ》

如果您还有什么疑惑或建议，欢迎在下方评论区继续讨论。

如果您觉得本文还不错，欢迎分享/打赏本文。打赏并非要从中获得收益，而是希望知道科学空间获得了多少读者的真心关注。当然，如果你无视它，也不会影响你的阅读。再次表示欢迎和感谢！

如果您需要引用本文，请参考：

苏剑林. (Feb. 04, 2013). 《[问题解答]双曲线上的最短距离》[Blog post]. Retrieved from https://spaces.ac.cn/archives/1904

@online{kexuefm-1904,
        title={[问题解答]双曲线上的最短距离},
        author={苏剑林},
        year={2013},
        month={Feb},
        url={\url{https://spaces.ac.cn/archives/1904}},
}